Раскрытие неопределенностей.

Если при подстановке предельного значения х в выражение под знаком предела получается величина вида [], [], [∞-∞], [1^∞], то говорят, что имеет место соответствующая неопределенность.

Способы устранения неопределенностей.

1. Алгебраические методы.

а) Разложение на множители. ==10. ([])

б) Устранение иррациональности. ([])

в) Выделение главного члена. ([])

2. Применение замечательных пределов.

а) при тригонометрических выражениях

б) при неопределенности [1^∞].

3. Метод эквивалентных б/м функций.

Примеры. С помощью замены эквивалентных найти пределы:

1) . Имеем ln(1+3x) ~3x, sin 5x~5x. Поэтому =

2) . Имеем ~x², ln(cosx)=ln(1+(cosx-1))~cosx-1. Поэтому ==-2

3) =====

==

Сравнение бесконечно больших величин.

Пусть функции А(х) и В(х) определены в некоторой окрестности V(x₀) точки х₀, за исключением, быть может самой точки х₀. Пусть (для определенности) функции А(х) и В(х) положительные бесконечно большие при х→х₀+0, т.е.

и

1. если , то функцию А(х) называется б.б. более низкого порядка по сравнению с В(х) при х→х₀+0.

2. если =с≠0, с≠, то функции А(х) и В(х) называются б.б. одного порядка при х→х₀+0.

3. если 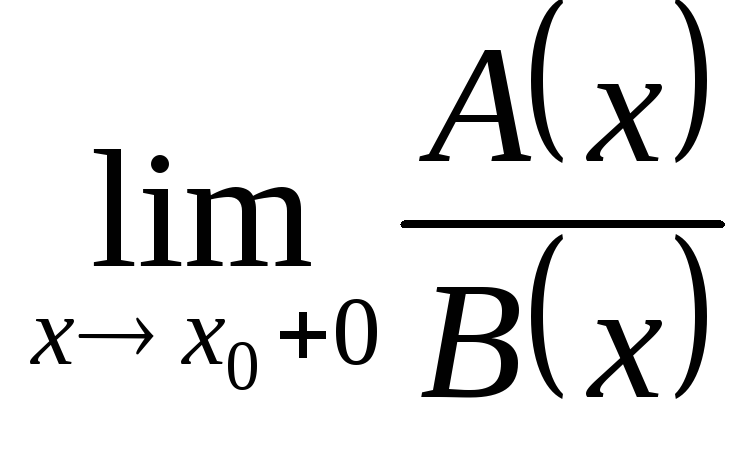=, то функцию А(х) называют б.б. более высокого порядка по сравнению с В(х) при х→х₀+0.

4. если отношение не имеет придела при х→х₀+0, то говорят, что б.б. функции α(х) и β(х) не сравнимы при х→х₀+0.

5. если =с≠0, с≠, то А(х) называется б.б. n –го порядка по сравнению с В(х) при х→х₀+0. (n>0, не обязательно целое).

Из предыдущих пунктов следует, что

1) Если n=1, то функция А(х) б.б. одного порядка с В(х) при х→х₀+0.

2) Если n>1, то функция А(х) б.б. более высокого порядка по сравнению с В(х) при х→х₀+0

3) Если n<1, то функция А(х) б.б. более низкого порядка по сравнению с В(х) при х→х₀+0

Пределы монотонных функций.

Теорема 1. (б.д.?)Пусть функция f(x) монотонно возрастает (строго возрастает) на множестве Х. Пусть в любой левой полуокрестности точки х₀ (х₀-;х₀) существуют точки множества Х, отличные от х₀. (Число х₀ может быть как конечным, так и равным +, в этом случае левая полуокрестность это хХ: x<x₀).

1) Если при этом функция f(x) ограничена сверху, т.е. существует число С такое, что f(x)С хХ, то при х→х₀-0 функция f(x) имеет конечный предел.

2) Если f(x) сверху не ограничена, то .

Доказательство.

1) Т.к. функция f(x) ограничена сверху, тогда существует точная верхняя граница множества {f(x)}, xX. Пусть m=. Тогда хХ f(x)m. (1)

Возьмем сколь угодно малое >0 и рассмотрим число m-.

Т.к. m-<m, то по свойству супремума на множестве {f(x)}, xX, обязательно найдется элемент >m-.

Т.к. функция f(x) монотонно возрастает на множестве Х, то хХ, удовлетворяющих условию х> будет f(x) и, следовательно, f(x)>m- (2).

Т.о. хХ: х> будут выполняться оба неравенства (1) и (2), т.е.

m-<f(x)m, значит, m-<f(x)m+ f(x)-m<.

а) Положим =а- или =а-, где а – конечное число. В этом случае хХ, удовлетворяющих неравенству а-<x<a, будет f(x)-m<, а это означает m=

б) Положим =, если а=+ (можно считать, что =>0). В этом случае хХ, удовлетворяющих неравенству x>, будет f(x)-m<, а это означает m=

2) (б.д.?) Допустим, что функция f(x) не ограничена сверху, т.е. не ограничено сверху множество {f(x)}, xX. Это значит, что какое бы большое число М>0 ни взять на множестве {f(x)}, xX, обязательно найдется хотя бы один элемент такой, что будет >М.

Т.к. функция f(x) монотонно возрастает на множестве Х, то хХ, удовлетворяющих условию х> будет f(x) и, следовательно, f(x)>М.

а) Положим =а- или =а-, где а – конечное число. В этом случае хХ, удовлетворяющих неравенству а-<x<a, будет f(x)>М, а это означает =+.

б) Положим =, если а=+ (можно считать, что =>0). В этом случае хХ, удовлетворяющих неравенству x>, будет f(x)>М, а это означает =+. Ч.т.д.

Теорема 2. Пусть функция f(x) монотонно убывает (строго убывает) на множестве Х. Пусть в любой левой полуокрестности точки х₀ (х₀-;х₀) существуют точки множества Х, отличные от х₀. (Число х₀ может быть как конечным, так и равным +, в этом случае левая полуокрестность это хХ: x<x₀).

1) Если при этом функция f(x) ограничена снизу, т.е. существует число М, такое, что f(x)М хХ, то при х→х₀-0 функция f(x) имеет конечный предел.

2) Если f(x) снизу не ограничена, то .