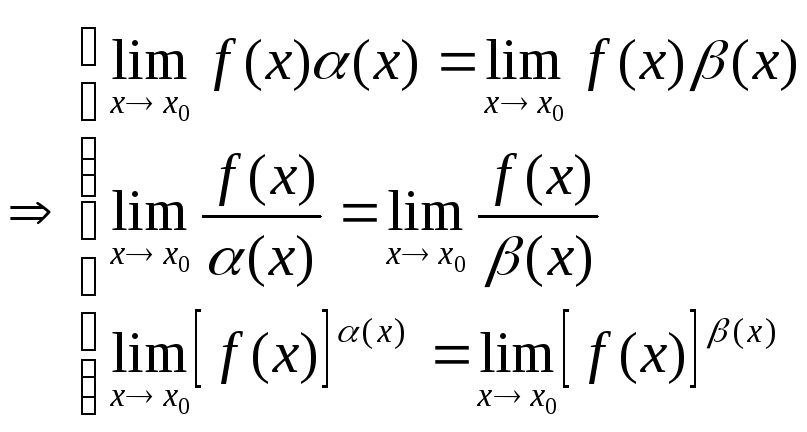Свойства б/б величин.

1. Если одна из трех функций f(x), -f(x), f(x) является б.б. при х→х₀, то и две другие функции также являются б.б. при х→х₀.

2. Произведение б/б функции на функцию, предел которой отличен от нуля, есть б/б величина.

3. Сумма б/б величины и ограниченной функции есть б/б величина.

4. Частное от деления б/б функции на функцию, имеющую предел, есть б/б функция.

Например, функция f(x)= - является частным от деления б/б функции tg x при х→П/2 на функцию 2х+5 имеющую предел П+5 при х→П/2.

Доказательство св-ва 2. (остальные – аналогично).

Пусть f(x) – б.б. функция при х→х₀, т.е. =∞ и =с (с≠0).

Докажем, что f(x)(х) - б.б. функция при х→х₀.

Рассмотрим последовательность х_n→x₀, n→ (предполагается, что x_n берутся из окрестности x₀ и x_n≠x₀)

По условию =с (с≠0). Но тогда и =с (с≠0).

По условию f(x) – б.б. функция при х→х₀, но тогда и f(x_n) – б.б. функция при n→. Следовательно, f(x_n)(х_n) - б.б. последовательность, как произведение б.б. последовательности и последовательности, имеющей конечный, отличный от 0 предел.

Т.к. последовательность х_n – любая сходящаяся к х₀, то заключаем, что

Это означает, что функция f(x)(х) - б.б. функция при х→х₀. ч.т.д.

Связь между б/б и б/м функциями.

Теорема. Если функция α(х) – б/м величина при х→х₀ (х→∞), то функция β(х)= является б/б при х→х₀ (х→∞). И наоборот, если функция β(х) – б/б величина при х→х₀ (х→∞), то функция α(х)= является б/м при х→х₀ (х→∞).

Доказательство. Пусть α(х) – б/м величина при х→х₀ (х→∞), тогда

ε > 0 δ=δ(ε)> 0 х: 0<|х–х₀|<δ |α(х)|<ε

Последнее неравенство равносильно неравенству > или |β(х)|>M, где М=, т.е. β(х) – б/б. Аналогично доказывается второе утверждение.

Сравнение бесконечно малых величин.

Пусть при х→х₀ функции α(х) и β(х) являются б.м., и пусть β(х)≠0 тогда

1. если , то α(х) называется б.м. более высокого порядка, чем β(х) (α(х) имеет более высокий порядок малости, чем β(х) при х→х₀)

Пишут (х)=о((х)) при х→х₀ (о малое)

Пример. Покажем, что при х→0 функция х^k (k>1) – б.м. более высокого порядка, чем х. Действительно, =0, т.к. по условию k>1.

2. если 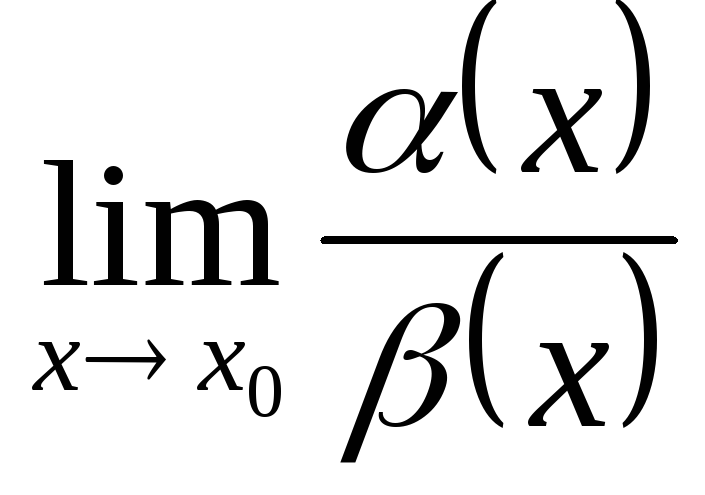=А≠0, то α(х) и β(х) называются б.м. одного порядка (имеют одинаковую «скорость» стремления к 0).

Пример. Покажем, что при х→0 функции sin kx и mx (k≠0,m≠0)- б.м. одного порядка. Действительно,

3. если =1, то α(х) и β(х) называются эквивалентными б.м.: α(х)~β(х).

Пример. Покажем, что при х→0 функции sin x и tg x (k≠0,m≠0)- б.м. одного порядка. Действительно,

4. если =, то функцию α(х) называют б.м. более низкого порядка по сравнению с β(х) при х→х₀.

5. если отношение не имеет придела при х→х₀, то говорят, что б.м. функции α(х) и β(х) не сравнимы при х→х₀.

Пример. Функции (х)= и (х)=х – б.м. при х→0. Имеем , но не имеет предела при х→0. Значит, α(х) и β(х) не сравнимы при х→0.

6. если =А≠0, то α(х) называется б.м. n –го порядка относительно β(х) при х→х₀. (n>0, не обязательно целое).

Из предыдущих пунктов следует, что

1) Если n=1, то функция α(х) б.м. одного порядка с β(х) при х→х₀.

2) Если n>1, то функция α(х) б.м. более высокого порядка по сравнению с β(х) при х→х₀.

3) Если n<1, то функция α(х) б.м. более низкого порядка по сравнению с β(х) при х→х₀.

Теорема 1. Произведение двух б.м. величин является б.м. величиной более высокого порядка по сравнению с каждым из сомножителей.

Доказательство. Пусть при х→х₀ функции α(х) и β(х) являются б.м., γ(х)=α(х)β(х). Докажем, что γ(х)=о(α(х)) и γ(х)=о(β(х)) при х→х₀. Имеем

, а это означает, что γ(х)=о(α(х)) при х→х₀.

Аналогично, , а это означает, что γ(х)=о(β(х)) при х→х₀. ч.т.д.

Теорема 2. Разность двух эквивалентных бесконечно малых функций является бесконечно малой функцией по сравнению с каждой из них.

Доказательство. Пусть при х→х₀ функции α(х) и β(х) являются б.м., и α(х)~β(х). Положим γ(х)=α(х)-β(х). Докажем, что γ(х)=о(α(х)) и γ(х)=о(β(х)) при х→х₀. Имеем

, По условию, т.к. α(х)~β(х), то =1. Следовательно, =1-1=0. Значит, γ(х)=о(α(х)) при х→х₀.

Аналогично, , По условию, т.к. α(х)~β(х), то =1. Следовательно, =1-1=0. Значит, γ(х)=о(β(х)) при х→х₀. ч.т.д.

Теорема 3 (о замене бесконечно малых при отыскании предела отношения).

Пусть функции α(х) и β(х) являются б.м. при х→х₀, и α(х)~(х), β(х) ~(х) при х→х₀. Тогда если существует конечный или бесконечный предел

,

То к этому же пределу стремится при х→х₀ и отношение .

Доказательство. 1) Пусть =с, где с – конечное число. Тогда очевидно следующее равенство: =

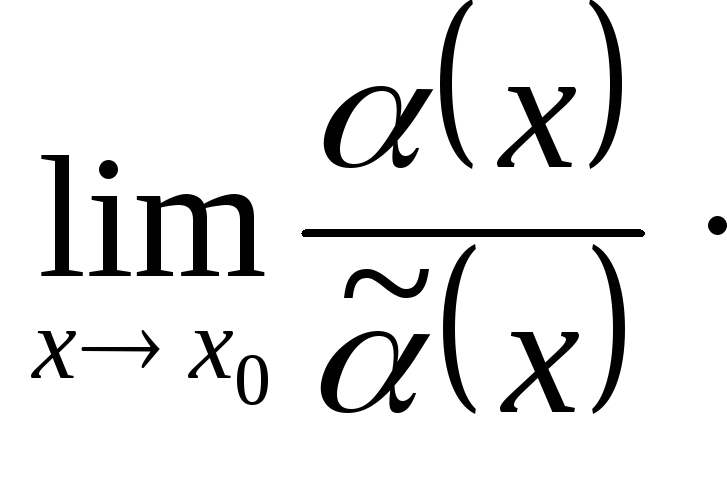
По условию, каждый из сомножителей в правой части имеет конечный предел при х→х₀. Тогда ==1с1=с. Т.е. =.

2) Пусть =. Но тогда =0 (считаем, что (х)≠0 ).

По доказанному в пункте 1), =0=.

Значит, и в этом случае = ч.т.д.

Замечание 1. Применение теоремы 3 требует знания б.м. функций (х) и (х) эквивалентных при х→х₀ бесконечно малым функциям α(х) и β(х).

1) sin x~x при х→0 (т.к. =0),

2) tg x~x, при х→0 3) 1-cos x~, при х→0

4) ln(1+x) ~x, при х→0 5) e^x-1~x, при х→0

6)a^x-1~xlna, при х→0 (a>0, a≠0)

7) (1+x)^a-1~ax, при х→0

8) arcsin x~x, при х→0 9) arctg x~x, при х→0

Покажем, что ln(1+x) ~x, т.е. =1

===ln (т.к. функция ln x непрерывна)=ln e=1. Ч.т.д.

Замечание 2. Теорему 3 можно также применять в следующих случаях:

Если выражение под знаком предела содержит б/м величину в виде множителя, в виде отношения или в виде показателя степени, то ее можно заменить на эквивалентную ей б/м.

α(х)~β(х)