Тема 3. Измерители и показатели финансового риска

Финансовая операция называется вероятностной, если существует вероятность каждого её исхода. Прибыль такой операции - разность конечной и начальной денежных её оценок - является случайной величиной. Для такой операции удается ввести количественную оценку риска, согласующуюся с нашей интуицией.

3.1. Количественная оценка риска и эффективность операций при вероятностной характеристике множества исходов операций

При исследовании риска операции встречаемся с фундаментальным утверждением:

Утверждение. Количественная оценка риска операции возможна только при вероятностной характеристике множества исходов операции.

Пример 1. Рассмотрим две вероятностные операции :

-5	25
0,01	0,99

15	25
0,5	0,5

: :

Несомненно, риск первой операции меньше риска второй операции. Что же касается того, какую операцию выберет ЛПР, это зависит от его склонности к риску.

Мы хотим количественно оценить рискованность операции, а это невозможно сделать без вероятностной характеристики операции, поэтому её исходам припишем вероятности и оценим каждый исход доходом, который ЛПР получает при этом исходе. В итоге получим случайную величину Q, которую естественно назвать случайным доходом операции, или просто случайным доходом. Пока ограничимся дискретной случайной величиной (Д.с.в.):

Где - доход, а - вероятность этого дохода, через Q обозначаем как операцию так и С.В. доходов.

Теперь можно применить аппарат теории вероятностей и найти следующие характеристики операции.

Средний ожидаемый доход – математическое ожидание С.В. Q, т.е обозначается еще , употребляется также название эффективность операции.

Дисперсия операции – дисперсия С.В. Q, т.е. , обозначается также ..

Среднее квадратическое отклонение С.В. обозначается также .

Отметим, что средний ожидаемый доход, или эффективность операции, как и среднее квадратическое отклонение измеряется в тех же единицах, что и доход.

Напомним что математическое ожидание это примерно среднее арифметическое значений, принятых С.В. в длинной серии опытов.

Все более признанными становится оценка рискованности всей операции посредством среднего квадратического отклонения случайной величины дохода Q, т.е. посредством . Мы будем считать это основной количественной оценкой риска.

Итак, риском операции называется число - среднее квадратическое отклонение случайного дохода операции Q, обозначается также через .

Пример 2. Найдем риски первой и второй операции из примера 1:

: :

-5	25
0,01	0,99

15	25
0,5	0,5

Сначала вычисляем математическое ожидание С.В. : m₁=-50,01+250,99=24,7. Теперь вычислим дисперсию по формуле . Имеем . Значит, и окончательно .

Аналогичные вычисления для второй операции дают ; . Как и подсказывала интуиция, первая операция менее рискованная.

Предполагаемая количественная оценка риска вполне согласуется с интуитивным пониманием риска как степени разбросанности исходов операции – ведь дисперсия и среднее квадратическое отклонение (квадратный корень из дисперсии) и суть меры такой разбросанности.

Пример 3. ЛПР рассматривает две возможные игры. В одной бросают монету, ЛПР получает 10 денежных единиц, если монета упадет «орлом» вверх, и платит 10 единиц, если она упадет «решкой» вверх. Выплаты в этой игре образуют ряд распределения слева:

В другой игре бросают игральный кубик и выплаты ЛПР образуют ряд распределения справа.

Средний ожидаемый выигрыш в обоих случаях равен 0. однако интуитивно разбросанность платежей во второй игре больше. Вычисления дисперсии и риска подтверждают это:

; ;

; .

Средний ожидаемый доход операции Q, т.е. ее эффективность и ее риск связаны известным неравенством Чебышева:

, или .

Однако известно, что это неравенство весьма грубое и на практике почти не применяется.

Если доход операции есть случайная величина, распределенная по нормальному закону, то риск довольно точно указывает некоторые вероятности, связанные с эффективностью:

. Иногда эти оценки весьма полезны.

Следующие утверждения о риске являются следствиями соответствующих утверждений о дисперсии и среднем квадратическом отклонении из теории вероятностей.

Утверждение. А. При увеличении масштаба операции в k раз, т.е. при увеличении всех значений случайного дохода в k раз, эффективность операции увеличивается в k раз, а риск – в раз.

Б. При изменение всех доходов на одно и то же постоянное число эффективность операции также изменяется на это число, а риск не изменяется.

В. Пусть операции Q₁ и Q₂ некоррелированы, тогда дисперсия их суммы равна сумме дисперсий, поэтому риск суммарный операции равен .

Г. В общем случае, т.е. для двух произвольных операций Q₁ и Q₂, риск суммарной операции равен , где k₁₂ - коэффициент корреляции случайных доходов операций; заметим, что ; из этой формулы вытекает, что риск суммарной операции не может быть больше величины .

Напомним, что случайные величины Х, Y называются некоррелированными, если их корреляционный момент равен 0; корреляционный момент и коэффициент корреляции связаны формулой ; независимые случайные величины некоррелированы.

Д. Если операция , то эффективность суммарной операции равна сумме эффективностей отдельных операций m_i, т.е. , а дисперсия и следовательно риск суммарной операции . Обозначим , , тогда учитывая что , получаем . В частности если операции некоррелированы, то .

Е. В случае, если возможные исходы операций заданы статистически, т.е. имеется ряд наблюдений , то математическое ожидание и среднеквадратическое отклонение заменяются их статистическими оценками. Поэтому эффективность операции , а , где - вариация Q (статистическая оценка дисперсии) .

Ж. При статистическом задании возможных исходов операций эффективность и риск суммарной операции определяются по формулам

, где , , .

Здесь - ковариация i-ой и j-ой операций - , а - вариация i-ой операции Q_i, т.е. . Обозначим , тогда риск операции Q можно записать в виде:

,

в частности для некоррелированных операций .

Пример 4. Пусть операции Q₁ и Q₂ некоррелированы, найдем риск операции (например, денег не хватит на проведение обеих операций в полном объеме):

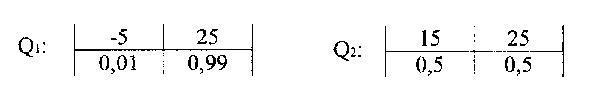
Риски обеих операций уже найдены в примере 2: =2,98; =5. Значит,

.