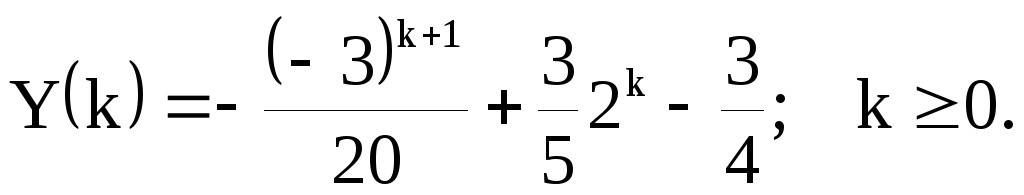лекции / lekcii_kompyuternoe_upravlenie / КУ_Л_06

ЛЕКЦИЯ № 6

ИСПОЛЬЗОВАНИЕ Z- ПРЕОБРАЗОВАНИЯ ДЛЯ АНАЛИЗА ПРОЦЕССОВ В ИМПУЛЬСНЫХ СИСТЕМАХ.

План лекции:

1. Свойства Z- передаточных функций (ПФ)

2. Пример получения Z-ПФ дискретной системы.

3. Определение процессов в импульсных смистемах.

4. Примеры расчета процессов в дискретных системах.

6.1Свойства Z-ПФ

1Z-ПФ есть дробно-рациональная функция переменного Z При использовании модифицированного Z-преобразования числитель этой функции зависит от , причем всегда соблюдается условие физической реализуемости (степень числителя не превосходит степень знаменателя)

2Полюсы , Z-ПФ w(z) и w(z,)связаны с полюсами ПФ НЧ соотношениями:

(6.1)

3Степень знаменателя W(z) (порядок дискретной ПФ) равна степени полинома знаменателя исходной ПФ:

4 Функция W(z) конечна при z=1, если ПФ W(p) не имеет полюсов в начале координат При W(z) стремится к вещественному числу

Пример №5.1:

Найдем Z-ПФ разомкнутой дискретной системы, состоящей из АИЭ с экстраполятором нулевого порядка и непрерывной части с ПФ .

Решение:

ПФ ПНЧ:

Воспользуемся вычетами для определения :

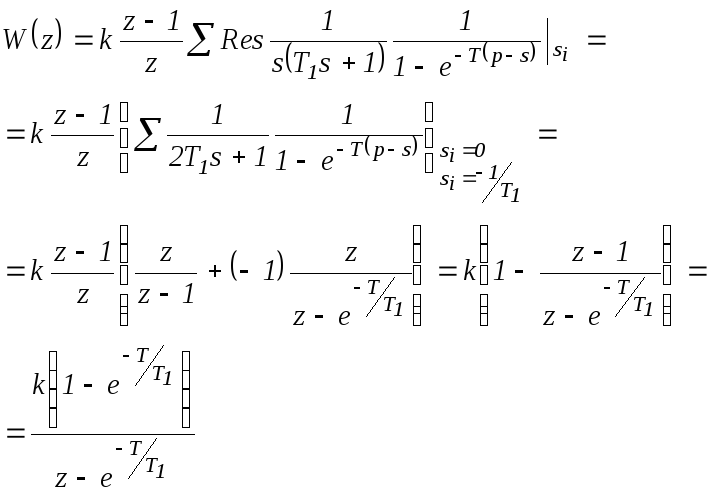
В случае, если воспользоваться разложением на простые дроби:

; ,

6.2Определение процессов в импульсных системах

с помощью Z-преобразования

Если известны ПФ импульсной системы W(z) и изображения входного сигнала F(z), то процесс на выходе системы может быть найден по формуле обратного Z- преобразования:

Обратное Z-преобразование можно определить с помощью вычетов:

,

где -полюсы функций, стоящих под знаком обратного преобразования

Для вычисления обратного Z-преобразования могут быть использованы рассмотренные выше методы степенных рядов (разложение в ряд Лорана, деление многочлена на многочлен и т д)

Наконец, по известной Z-ПФ, достаточно просто составить соответствующее разностное уравнение импульсной системы

Пусть

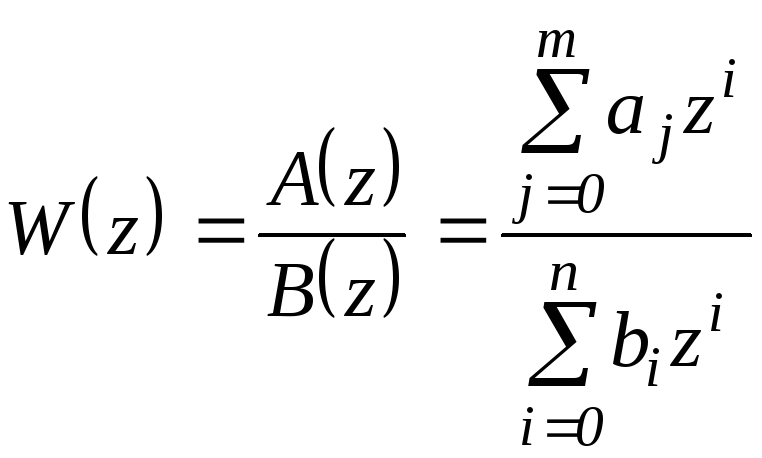
Но, так как

,

то

.

Тогда:

.

Учитывая теорему о смещении аргумента решетчатой функции:

(при нулевых начальных значениях), получим:

Это соотношение представляет собой рекуррентное уравнение Оно позволяет рассчитывать процессы на выходе системы, в последующие моменты времени по известным предыдущим значениям

Пример№5.2:

Решение:

Перейдем к оригиналам, учитывая теорему о смещении аргумента решетчатой функции:

отсюда:

тогда при известных начальных условиях:

Пример№5.3:

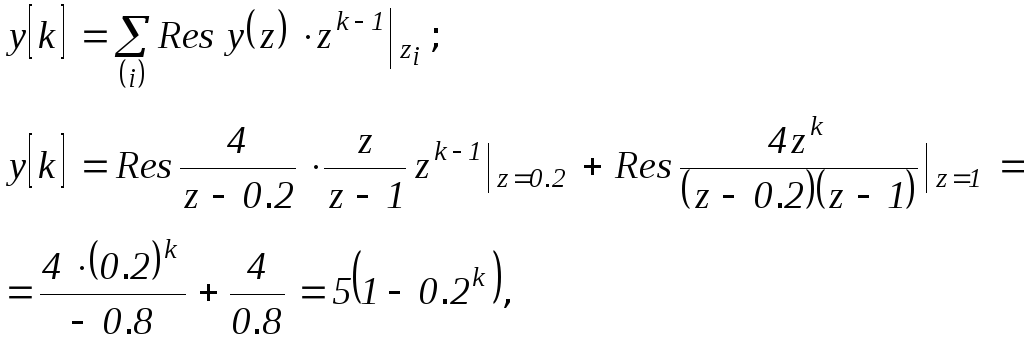
Численные значения:



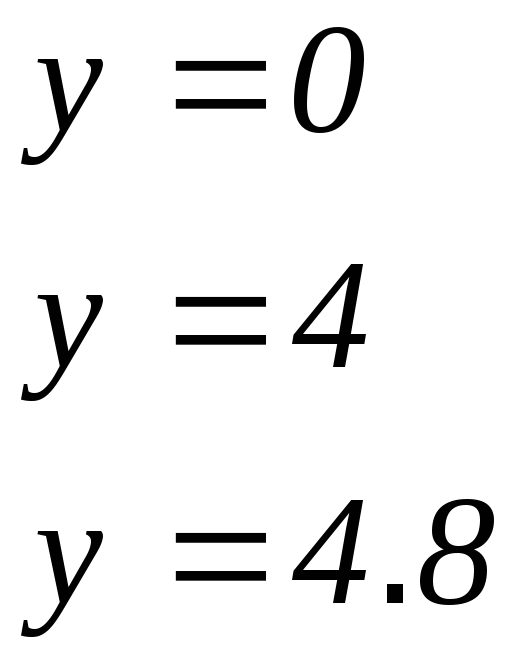
Пример№5.4:

2Переход к конечноразностному уравнению:



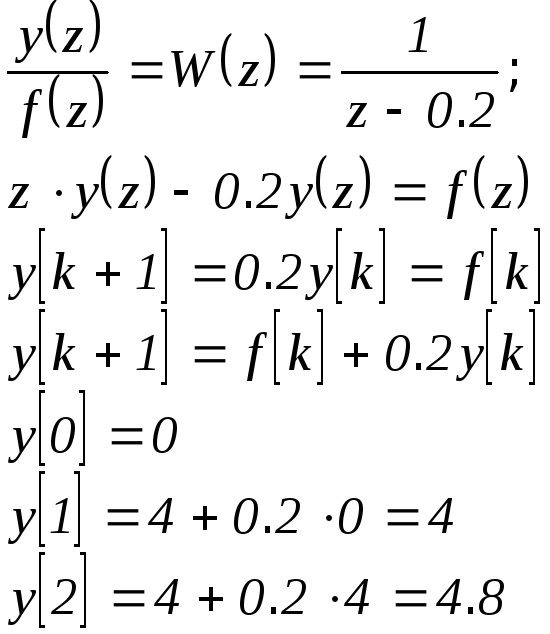
Пример№5.5:

Пусть линейная стационарная дискретная система описывает разностным уравнением:

.

Найти выходную функцию при условии, что система сначала находится в покое и входное воздействие есть:

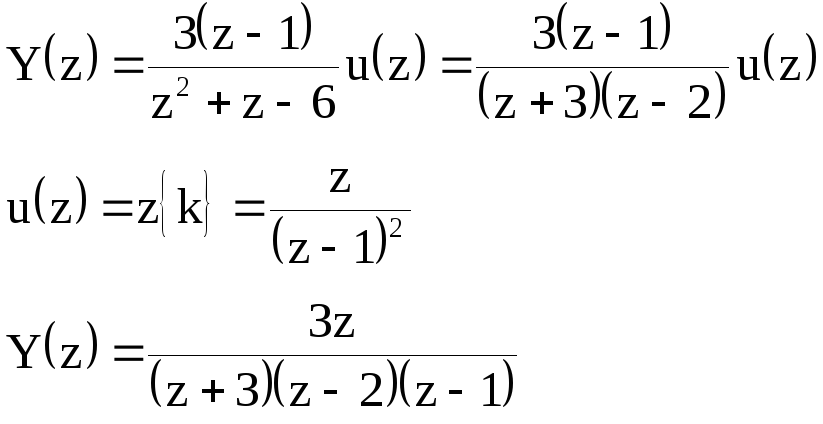
Обратное преобразование найдем по теореме о вычетах.

Полюсы:

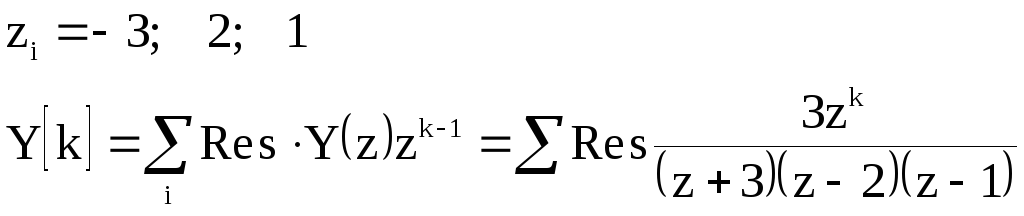
Вычеты в точках :

Следовательно:

38