ЛЕКЦИЯ №10

ЧАСТОТНЫЕ СВОЙСТВА ИМПУЛЬСНЫХ СИСТЕМ

План лекции:

1. Преобразование спектра непрерывного гармонического сигнала импульсным элементом.

2. Частотное представление решетчатой функции.

3. Прохождение непрерывного гармонического сигнала через дискретно-непрерывную цепь

10.1 Преобразование спектра непрерывного гармонического сигнала импульсным элементом

Рассмотрим прохождение гармонического сигнала через дискретную систему Напомним, что в непрерывном случае, входному гармоническому сигналу соответствует входной гармонический сигнал той же частоты, те качественного изменения спектра не происходит

Дискретная система в отличие от непрерывной изменяет спектр входного сигнала, вводит в него дополнительные составляющие

Для иллюстрации сказанного рассмотрим простейший пример: Определим реакцию дискретной системы с ПФ: на гармонический входной сигнал f=cos0907t. Такую ПФ имеет система, структурная схема которой представлена на рис.10.1.

f f* y(t)

Рис.10.1.

Параметры системы: , интервал квантования 0,693.

На периоде входного сигнала укладывается 10 таких интервалов

; ;

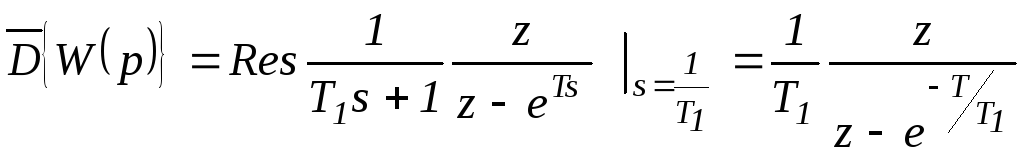; ; Т₁=1;

Для рассматриваемой z-ПФ ранее были построены частотные характеристики и мы их используем сейчас для определения реакции на дискретный сигнал

Получим:

Выходной сигнал, рассматриваемый в моменты квантования, будет иметь вид:

Полученная формула определяет реакцию системы лишь в дискретные моменты времени, а нас интересует вид всего выходного процесса при произвольном аргументе t

Для построения графика установившегося процесса будем действовать в такой последовательности:

1. Из последней формулы найдем начальное значение

, соответствующее искомому процессу

2) На интервале , и выходная величина в соответствии с известными зависимостями для апериодического звена определится выражением:

, при этом

3)В момент t=T на вход непрерывной части действует -функция:



Она вызывает скачок выходной переменной , при этом:

.

В дальнейшем, при процесс вычисления выходной переменной аналогичен описанному в п2 и 3 Во внутренних точках каждого интервала квантования входной сигнал описывается зависимостью:

,

а в точках , сигнал терпит разрыв и при этом

Таким образом, строится график установившегося процесса (рис.10.2).

Из рисунка видно, что решетчатая функция y[nT], рассматриваемая в дискретные моменты квантования, является гармонической Тем не менее, сам процесс гармоническим не является, те дискретная система изменяет спектр входного сигнала

Причина такого изменения с формальной точки зрения становится понятной, если вспомнить связь между изображением решетчатой функции f[nT] и преобразованием Лапласа исходной непрерывной функции f(t) Эта связь задается известной формулой - преобразования:

.

Р ис.10.2.

Из этой зависимости непосредственно следует, что если

,

то

(10.1)

те процесс квантования сопровождается возникновением бесконечного множества дополнительных гармонических составляющих, каждая из которых далее преобразуется непрерывной частью системы

10.2 Частотное представление решетчатой функции

Пусть теперь f(t) – некоторая непрерывная преобразуемая по Фурье функция. F(j)

Прямое и обратное преобразование Фурье

для этой функции имеет вид (рис.10.3):

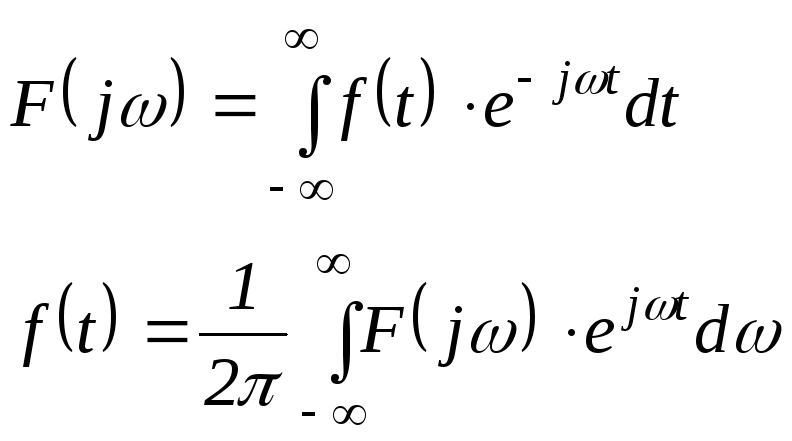
Рис.10.3.

Допустим, при этом, что спектральная характеристика указанного непрерывного сигнала имеет вид, представленный на рис.10.4.

Рассмотрим спектр соответствующей решетчатой функции

В соответствии с формулой - преобразования он определяется зависимостью:

(10.2)

где - частота квантования

Как видно из (10.2) частотный спектр включает спектр входной величины (основной спектр) и боковые (дополнительные) спектры, смещенные по оси частот на величины, кратные  При этом дополнительные спектры идентичны основному (рис.10.4)

Рис.10.4

Полезная информация о входном сигнале содержится лишь в основном спектре и может быть восстановлена фильтрацией нежелательных составляющих, если дополнительные спектры не перекрываются с основным Это возможно, если входной сигнал не содержит составляющих, частота которых больше половины частоты квантования

(10.3)

где - максимальная частота спектра 

Это утверждение находится в согласии с теоремой Котельникова об эквивалентности непрерывного и дискретного сигналов

Напомним теорему:

Полное восстановление непрерывного сигнала по его импульсной последовательности возможно, если частота повторения импульсов по крайней мере в два раза больше максимальной частоты спектра этого сигнала

В случае нарушения условий теоремы основной и дополнительный спектры перекрываются и полезная информация не может быть извлечена из импульсного сигнала

В импульсных системах функцию фильтра низких частот в основном выполняют элементы самой системы, находящиеся в цепи импульсного элемента Для достижения лучшего эффекта фильтрации на выходе ИЭ могут включаться дополнительные сглаживающие фильтры

При этом с уменьшением частоты квантования обеспечить качественную фильтрацию становится все труднее При увеличении же частоты импульсов проблема фильтрации отпадает, так как в этом случае импульсная система приближается к непрерывной

Выбор компромиссного решения, обеспечивающего качественную фильтрацию и приемлемые процессы, составляет один из основных моментов при расчете импульсных систем

Наиболее простым и часто применяемым низкочастотным фильтром является экстраполятор нулевого порядка При этом решетчатая функция в качестве огибающей имеет ступенчатую функцию Эта огибающая содержит полезную информацию о сигнале на входе ИЭ ПФ экстраполятора нулевого порядка имеет вид:

;

Рассмотрим его АФЧХ:

По известной формуле: ,



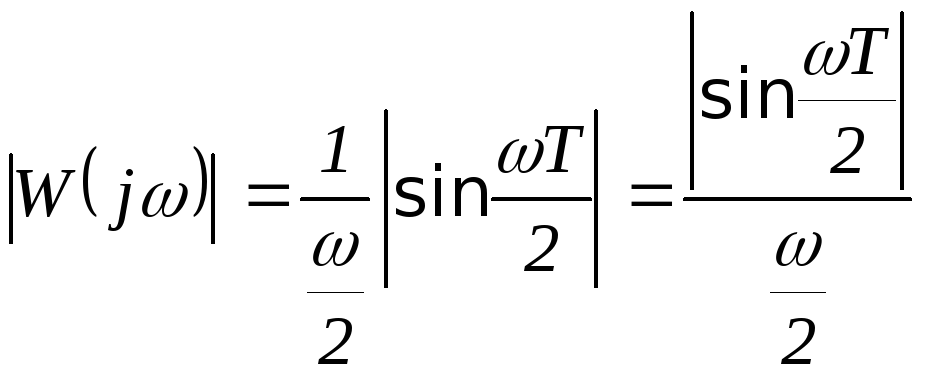
График представлен на рис.10.5:

Р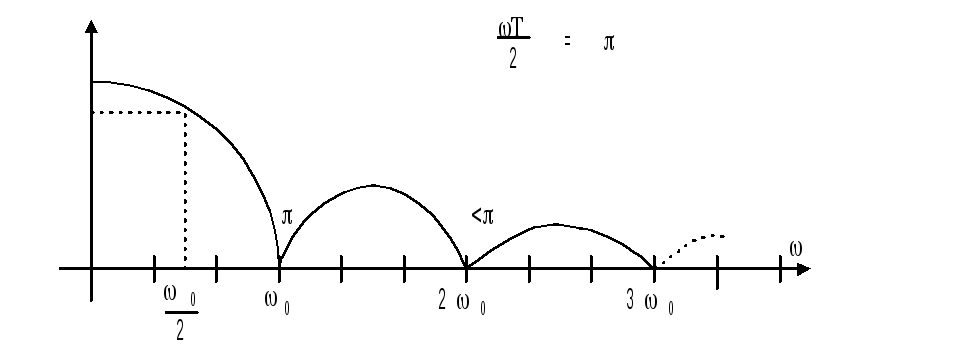 ис.10.5.

Из анализа приведенного графика, следует, что экстраполятор будет пропускать помимо основных составляющих спектра сигнала еще и боковые составляющие

10.3Прохождение непрерывного гармонического сигнала через дискретно-непрерывную цепь

Частотные характеристики дискретной системы не позволяют полностью определить ее реакцию на гармоническое входное воздействиеПри прохождении через ИЭ спектр сигнала изменяется, в нем появляются дополнительные составляющиеЭта особенность может оказать существенное влияние на работу импульсной системы

При прохождении сигнала через идеальный ИЭ на выходе будем иметь:

Из формулы (10.3) видно, что при этом возможно либо преобразование сигнала в высокочастотную область (при m>0), либо транспонирование высокочастотного входного сигнала в низкочастотную часть спектра (m<0).

В цифровых системах управления эффект транспонирования колебаний в низкочастотную область может привести к низкочастотным колебаниям на выходе объекта при действии высокочастотной помехи

Снижение величины транспонированных колебаний является важной задачейОбычно для ее решения используется предимпульсная фильтрация, т е фильтрация непрерывного сигнала до входа ИЭ Эффект такой фильтрации заключается в уменьшении амплитуды помехи, попадающей на ИЭВыбором параметров предимпульсного фильтра можно существенно уменьшить транспонированные колебания

68