
- •Статистика Учебное пособие.
- •Содержание (часть 1)
- •Глава 1. Методология и основные понятия статистики.
- •Основные понятия статистики.
- •1.2. Статистическое наблюдение.
- •1.3. Сводка и группировка статистических данных.
- •1.4. Представление статистических данных.
- •1.4.1. Статистические таблицы.
- •1.4.2. Графическое изображение статистических данных.
- •1.4.3. Решение типовых задач.
- •Глава 2. Статистические показатели.
- •2.1. Абсолютные величины.
- •2.2. Относительные величины.
- •2.3. Средние величины.
- •2.3.1. Структурные средние.
- •2.3.2. Степенные средние.
- •Глава 3. Показатели вариации.
- •3.1. Абсолютные и относительные показатели.
- •3.3. Показатели конкуренции.
- •Глава 4. Выборочное наблюдение.
- •4.1. Выборочная совокупность (выборка) и способы её отбора.
- •4.2. Оценка математического ожидания (средней величины).
- •4.3. Оценка вероятности или доли элементов генеральной совокупности, обладающих определенным признаком.
- •Глава 5. Корреляционная связь и ее анализ.
- •5.1. Корреляционно-регрессионный анализ.
- •5.1.1. Уравнение регрессии.
- •5.1.2. Коэффициент корреляции.
- •5.1.3. Оценка уравнения регрессии.
- •5.2. Непараметрические показатели связи.
- •5.2.1. Коэффициенты ранговой корреляции.
- •5.2.2. Анализ связи атрибутивных признаков.
- •5.2.3. Анализ связи альтернативных признаков.
- •Глава 6. Статистическое изучение динамики.
- •6.1. Виды рядов динамики. Средний уровень ряда динамики.
- •6.3. Выявление основной тенденции ряда динамики.
- •6.4. Сезонные колебания.
- •Глава 7. Экономические индексы.
- •7.1. Виды экономических индексов.
- •7.2. Общие индексы средних величин.
- •Глава 8. Экспертное оценивание.
- •8.1. Организация экспертизы.
- •8.2. Обработка и анализ результатов экспертизы.
- •8.2.1. Ранжирование объектов.
- •8.2.2. Оценивание по балльной шкале.
- •8.2.3. Парные сравнения.
2.3. Средние величины.
Средняя величина (СВ) – это показатель, характеризующий типичный уровень явления и выражающий величину признака, отнесенную к элементу совокупности. Их делят на два класса:
• структурные средние (мода и медиана);
• степенные средние (средняя арифметическая, средняя геометрическая и др.).
2.3.1. Структурные средние.
Мода (Мо)– это наиболее часто
встречающееся (т.е. с наибольшей частотой),
значение признака у элементов совокупности.
Если признак дискретная величина, мода
равна значению, которое повторяется
наиболее часто. Например, в группе из
11 студентов получены следующие баллы
за тест: 5, 4, 3, 7, 9, 5, 6, 2, 5, 6. Мода равна
пяти, т.к. число 5 встречалось наиболее
часто. Другой пример. Имеются данные о
размере обуви 11 девочек: 5, 3, 4, 3, 5, 4, 3, 4,
2, 6, 2. Поскольку наибольшую частоту имеют
два соседних размера обуви 3 и 4, то
модальное значение будет равно
 .
.
Модальным интервалом называется интервал, которому соответствует наибольшая частота. Для интервального ряда с равными интервалами, мода определяется по формуле:
 ,
(2.4)
,
(2.4)
где
 -
начальная граница модального интервала;
-
начальная граница модального интервала;
 – величина модального интервала;
– величина модального интервала;

 -
частота модального интервала, частота
интервала, предшествующего модальному,
и частота интервала, следующего за
модальным, соответственно.
-
частота модального интервала, частота
интервала, предшествующего модальному,
и частота интервала, следующего за
модальным, соответственно.
|
Пример 2.5. Определить моду ряда распределения роста группы девочек:
 . .
|
Медианой распределения называется
такое значение величины признака,
которое делит упорядоченную
последовательность его значений на две
равные по численности части; причем у
одной половины единиц совокупности
значение признака не превышает медианного
уровня, а у другой – выше этого значения.
Медиана дискретного ряда распределения
в случае нечетного числа членов
 соответствует
соответствует
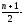 му
значению ряда, а в случае четного числа
членов
му
значению ряда, а в случае четного числа
членов
 медиана равна среднему арифметическому
медиана равна среднему арифметическому
 го
и
го
и
 го
значений ряда распределения. В случае
интервального ряда распределения
сначала определяют медианный интервал,
т.е. такой интервал, в котором сумма
накопленных частот превышает половину
общего числа наблюдений, а затем численное
значение медианы определяется по
формуле:
го
значений ряда распределения. В случае
интервального ряда распределения
сначала определяют медианный интервал,
т.е. такой интервал, в котором сумма
накопленных частот превышает половину
общего числа наблюдений, а затем численное
значение медианы определяется по
формуле:
 ,
(2.5)
,
(2.5)
где
 нижняя
граница медианного интервала,
нижняя
граница медианного интервала,
 – величина медианного интервала,
– величина медианного интервала,
 накопленная
частота интервала, предшествующего
медианному,
накопленная
частота интервала, предшествующего
медианному,
 частота
медианного интервала.
частота
медианного интервала.
|
Пример 2.6. Найдем медиану ряда
распределения роста девочек по данным
таблицы из примера 2.5. Здесь медианный
интервал 164 <
|

 < 168. Поэтому имеем:
< 168. Поэтому имеем: .
.