1.4.2. Графическое изображение статистических данных.

Графическое представление статистических показателей придает им наглядность и выразительность, облегчает их восприятие, помогает уяснить сущность изучаемого явления, его закономерности и особенности.

По способу построения графики подразделяют на:

диаграммы – это изображение статистических данных с помощью геометрических фигур, линий и точек;

картограммы – это географическая (контурная) карта, которая графически описывает пространственное распределение определенного статистического показателя путем различной окраски, штриховки и т.д., например, плотность населения в различных регионах земного шара.

Диаграммы бывают секторные, ленточные, столбиковые и линейные.

Основной формой структурных диаграмм являются секторные диаграммы (рис. 1.1).

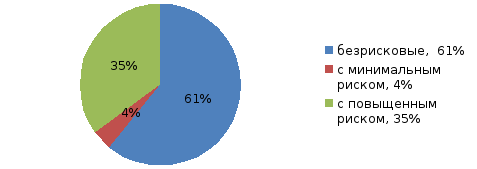
Рис. 1.1. Структура активов коммерческого банка по степени риска.

Пример ленточной диаграммы (рис. 1.2):

Рис. 1.2. Запасы нефти в отдельных странах в 2009 г.

Ленточная диаграмма особенно удобна в тех случаях, когда отдельные объекты сравнения характеризуются противоположными по знаку показателями (рис. 1.3).

Рис. 1.3. Прирост добычи нефти в отдельных странах в 2008 г. по сравнению с 2003 г.

Для изображения экономических явлений, протекающих во времени, применяют динамические диаграммы (рис. 1.4.).

Рис. 1.4. Уровень средней цены акций на бирже, руб.

Составной частью сводной обработки данных статистического наблюдения является построение рядов распределения, которые называются вариационными рядами. Отдельные значения признака называются вариантами, абсолютное число случаев повторения для каждого из вариантов, называются частотами; частостью (или относительной частотой) называется отношение доли частоты с данным значением к объёму выборки (к сумме всех частот): , где . По характеру вариации различают дискретные и непрерывные признаки. Ряды распределения дискретного признака изображаются в виде частотного полигона, а ряды распределения непрерывного признака – в виде гистограммы. Пример частотного полигона (синяя линия) приведен на рис. 1.5.

Рис. 1.5. Распределение квартир по числу проживающих в них

(частотный полигон и кумулянта).

Гистограмма – это столбиковая диаграмма, для построения которой на оси абсцисс откладывают отрезки, равные величине интервалов вариационного ряда; на отрезках строят прямоугольники, высота которых в принятом масштабе по оси ординат соответствует частотам, деленным на длину интервала. Общая площадь под гистограммой равна 1.

Для изображения и сравнения вариационных рядов как дискретного, так и непрерывного признака (например, для анализа концентрации производства или распределения числа предприятий по фондовооруженности труда рабочих) используется кумулятивная кривая – кумулянта. Для построения кумулянты, отражающей нарастание частот от группы к группе, значения варьирующего признака откладываются по оси абсцисс, а на оси ординат помещаются накопленные частоты (т.е. нарастающие итоги частот). Ордината кумулятивного графика показывает, сколько единиц или какая часть совокупности имеет значение признака, не превосходящее указанного на оси абсцисс. Пример кумулянты (красная линия) приведен на рис. 1.5.

Если при построении кумулятивной кривой поменять оси местами, получиться огива. Для данных, использованных при построении кривых на рис. 1.5, огива приведена на рис. 1.6.

Рис. 1.6. Распределение квартир по числу проживающих в них (огива).