Глава 6. Статистическое изучение динамики.

Социально-экономические явления общественной жизни находятся в непрерывном развитии, т.е. в динамике. Их изменения во времени в статистике изучается при помощи построения и анализа рядов динамики (их также называют динамическими, временными или хронологическими рядами).

6.1. Виды рядов динамики. Средний уровень ряда динамики.

Ряд динамики – это последовательность упорядоченных во времени значений статистических показателей, характеризующих уровень развития исследуемого явления. Элементами динамического ряда являются два ряда чисел: время и конкретное значение показателя или уровень ряда . Уровни выражаются в виде абсолютных, относительных и средних величин статистических показателей. Различают моментные и интервальные ряды динамики. У моментных рядов уровни характеризуют объёмы явления в определенные моменты времени (например, показатели численности населения на начало года, величины запаса какого-либо материала на начало периода), а у интервальных рядов уровни характеризуют объёмы явления за какие-то периоды (например, ряды показателей объёма продукции по месяцам года, количества отработанных человекодней по отдельным периодам). Если уровни интервального ряда представляют собой абсолютные величины, то их уровни можно суммировать или дробить во времени, получая новые численные значения объёма явления. Уровни же моментных динамических рядов суммировать нельзя; сумма не имеет смысла, так как каждый последующий уровень полностью или частично включает в себя предыдущий уровень. Однако разность уровней имеет смысл, характеризуя увеличение или уменьшение уровня ряда между датами учета.

Важнейшим условием правильного формирования рядов динамики является сопоставимость уровней, образующих ряд, т.е. осуществление смыкания рядов динамики.

Пример 6.1. Объём инвестиций по фирме характеризуется следующими данными: Период, годы 1987-1992 1993-1996 1997-1999 2000 Объем капитальных вложений, млн. руб. 840,7 420,8 540,3 200,5 Приведенный ряд дает неправильное представление о динамике инвестиций, так как показатели относятся к периодам с различной продолжительностью. Чтобы выявить изменение объёма, следует определить величину капитальных вложений на одну и ту же единицу каждого периода. Объём капитальных вложений за один год составляет: 1987–1992 гг. – ; 1993–1996 гг. –; 1997–1999 гг. – ; 2000 г. – 200,5. Как видно из этих данных, объём капитальных вложений снижался до 1997 г., и лишь начиная с 1997 г. наметилось некоторое его повышение.

Пример 6.2. Общий объём продукции в одном из регионов (в млн. руб.): Продукция промышленности Годы 1991 1992 1993 1994 1995 1996 1997 В старых границах региона В новых границах региона 20,1 20,7 21,0 21,2 23,8 24,6 25,5 27,2 Здесь показатели за 1991 –1993 гг. не сопоставимы непосредственно с показателями 1995 – 1997 гг., так как относятся к различным границам региона. Для приведения ряда динамики к сопоставимому виду для 1994 г. определим коэффициент соотношения уровней двух рядов: . Умножив на этот коэффициент уровни первого ряда, получают скорректированные данные за 1991 – 1993 гг. в новых границах. Таким образом, сопоставимый ряд динамики имеет вид: Уровни продукции промышленности Годы 1991 1992 1993 1994 1995 1996 1997 В новых границах региона 22,5 23,2 23,5 23,8 24,6 25,5 27,2

Методы расчета среднего уровня ряда зависят от его вида и способов получения статистических данных. В интервальном ряду с равноотстоящими уровнями расчет среднего уровня ряда производится по формуле простой средней арифметической:

(6.1)

где уровни ряда; число уровней ряда.

Если интервальный ряд имеет не равноотстоящие уровни, то средний уровень вычисляется по формуле взвешенной средней:

(6.2)

где длительность периода времени, в течение которого ряд имел уровень .

Для моментного ряда с равноотстоящими уровнями средний уровень ряда рассчитывается с помощью средней хронологической:

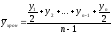, (6.3)

где – число уровней ряда.

Пример 6.3. Рассмотрим моментный динамический ряд: товарные запасы в торговом предприятии на начало каждого месяца характеризуются следующими данными: Время январь февраль март апрель Товарные запасы, млн.руб. 120 140 150 160 Средние товарные запасы за 1-й квартал, можно найти, используя формулу средней хронологической (6.3): млн. руб. От моментного ряда можно перейти к интервальному ряду. Для этого определим средние запасы за месяц: за январь: млн. руб.; за февраль: млн. руб.; за март: млн. руб. Время январь февраль март Товарные запасы, млн.руб. 130 145 155 Средние запасы за 1-й квартал рассчитываем, используя формулу простой средней арифметической (6.1): млн. руб.

Для моментного ряда с неравными интервалами предварительно находятся значения уровней в серединах интервалов: а затем определяется средний уровень ряда:

. (6.4)

Пример 6.4. Товарные запасы на начало каждого месяца характеризуются следующими данными: Время январь март апрель Товарные запасы, млн.руб. 120 150 160 Определяем средние запасы за интервал: млн. руб.; млн. руб. Вычислим средние товарные запасы за 1-й квартал (11.4): млн. руб.

 6.2. Аналитические показатели динамики.

Развитие явления во времени характеризуют следующие основные показатели динамики: абсолютные приросты, коэффициенты роста, темпы роста и темпы прироста. Эти показатели можно исчислять с переменной и постоянной базой. Если производится сравнение каждого уровня с предыдущим уровнем, то получаются показатели динамики с переменной базой – цепные показатели динамики. Если каждый уровень сравнивается с начальным уровнем или каким-то другим, принятым за базу сравнения, то получаются показатели динамики с постоянной базой – базисные показатели динамики. База сравнения должна выбираться обоснованно, в зависимости от экономических особенностей изучаемого явления и задач исследования.

При расчете показателей приняты следующие обозначения:

уровень текущего периода (уровень ряда);

уровень предшествующего периода;

уровень, принятый за базу сравнения (базисный уровень).

Абсолютный прирост - это разность между двумя уровнями ряда. Он показывает, на сколько в абсолютном выражении уровень текущего периода больше (меньше) предыдущего или базисного:

. (6.5)

Коэффициент роста - это отношение текущего уровня к предыдущему или базисному:

. (6.6)

Темп роста – это коэффициент роста, выраженный в процентах:

. (6.7)

Он показывает, сколько процентов текущий уровень составляет по отношению к предыдущему или базисному уровню.

Темп прироста - это отношение абсолютного прироста к предыдущему или базисному уровню:

. (6.8)

Темпы прироста часто выражают в процентах.

Для характеристики динамики явлений в ряде случаев используются пункты роста (%), представляющие собой разность темпов прироста с постоянной базой двух смежных периодов.

Пример 6.5. Расчет темпов роста, темпов прироста и пунктов роста иллюстрируется следующей таблицей: Показатель 1998 г. 1999 г. 2000 г. 2001 г. Уровень ряда 200 220 245 254 Темп роста с постоянной базой, % – 110 122,5 127 Темп прироста с постоянной базой, % – 10 22,5 27,0 Пункты роста, % – – 12,5 4,5

Пример 6.6. Имеются следующие данные о розничном товарообороте торгового дома по годам: Годы 2000 2001 2002 2003 Товарооборот, млн руб. 1100 1600 2000 4000 Необходимо определить показатели динамики розничного товарооборота. Результаты вычислений основных показателей торгового дома по формулам (6.5) – (6.8) приведены в таблице. Годы Товарооборот, млн руб Абсолютный прирост, млн.руб. Темпы роста, % Темпы прироста, % базисный цепной базисный цепной базисный цепной 2000 1100 - - - - - - 2001 1600 1600-100=500 1600-1100=500 1600·100/1100 =145 1600·100/1100 =145 45 45 2002 2000 2000-100=900 2000-1600=400 2000·100/1100 =182 2000·100/1600 =125 82 25 2003 4000 4000-1100=2900 4000-2000=2000 4000·100/1100 =364 4000·100/2000 =200 264 100

Для характеристики интенсивности развития за длительный период рассчитываются средние показатели динамики. Кроме среднего уровня, определяемого по формулам (6.1) – (6.4), к ним относятся средний абсолютный прирост, средний темп роста и прироста.

Для исчисления среднего абсолютного прироста используется следующая формула:

, (6.9)

где сумма цепных абсолютных приростов (по годам, если вычисляется среднегодовой абсолютный прирост), – число цепных приростов или число периодов, и – конечный и базисный уровни ряда.

Средний коэффициент роста исчисляется следующим образом:

. (6.10)

Средний темп роста рассчитывается как

. (6.11)

Средний темп прироста получается из среднего темпа роста

. (6.12)

Средний темп роста, рассчитанный по данным о конечном и начальном уровнях ряда динамики, используется лишь в случае более или менее равномерного изменения уровней. Особую осторожность при применении средних абсолютных приростов или средних темпов роста (прироста) следует соблюдать в тех случаях, когда появляется перелом в имевшей место тенденции изменения уровней динамического ряда.

Пример 6.7. По данным примера 6.6 определим средние абсолютный прирост, темп роста и прироста за 3 года. Среднегодовой абсолютный прирост находим по формуле (6.9) или . Средний коэффициент роста (6.10) , следовательно, , а . Розничный товарооборот за период с 2000 по 2003 год в среднем возрастал за год на 53,8%, в абсолютном выражении – на 967 млн. руб.