4.3. Оценка вероятности или доли элементов генеральной совокупности, обладающих определенным признаком.

Выборочная доля (или оценка вероятности) определяется как отношение числа элементов выборки с изучаемым признаком к её общему объёму :

. (4.12)

Выборочная дисперсия доли определяется величиной

. (4.13)

Величина предельной ошибки для доли равна:

• повторная выборка

, (4.14)

• бесповторная выборка

. (4.15)

Минимальный объём выборки, который обеспечивает требуемую точность, находят по формуле

. (4.16)

Пример 4.4. Имеется совокупность 10 000 деталей, произведенных на двух предприятиях. Для определения доли деталей, произведенных на первом предприятии, осуществили случайный бесповторный отбор 100 деталей. В выборке оказалось 20 деталей, произведенных на первом предприятии. Определить: 1) двусторонний доверительный интервал для доли, если уровень значимости ; 2) требуемый объем выборки, если предельная ошибка . Решение. 1) Выборочную долю и дисперсию определяем по (4.12) и (4.13):  ; . Предельную ошибку находим по (4.15) для . Как видно для условий примера практически нет разницы между повторным и бесповторным отбором. Левая и правая границы равны: . Можно утверждать, что с вероятностью 0,95 выполняется . 2) Если и , то получим (9.16): ; то есть .

Глава 5. Корреляционная связь и ее анализ.

5.1. Корреляционно-регрессионный анализ.

5.1.1. Уравнение регрессии.

В экономике в большинстве случаев между переменными величинами существуют зависимости, когда каждому значению одной переменной соответствует определенное (условное) распределение другой переменной. Такая связь называется статистической. В силу неоднозначности такой связи зависимость рассматривают в среднем, то есть, усредняя при большом числе наблюдений.

Если эта зависимость такова, что каждому значению одной переменной соответствует определенное условное среднее значение (математическое ожидание) другой, то ее называют корреляционной.

Независимую переменную называют факторной или фактором, а зависимую – называют результативной переменной. Связь двух переменных и называется парной корреляцией. Влияние же нескольких факторов 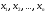на результативную переменную называется множественной корреляцией. Корреляция может быть положительной, когда с увеличением признака увеличивается и признак (например, автоматизация труда способствует росту рентабельности производства), и отрицательной, когда, наоборот, с увеличением признака признак уменьшается (так, с увеличением уровня фондоотдачи снижается себестоимость единицы производимой продукции).

Корреляционная зависимость описывается уравнением регрессии. Для его точного описания необходимо знать условный закон распределения зависимой переменной при условии, что фактор примет значение . На практике такой информации получить не удается, так как обычно имеется лишь выборка пар значений ограниченного объема . В этом случае речь может идти о приближенном выражении уравнения регрессии:

, (5.1)

где условная (групповая) средняя переменной при фиксированном значении ;

параметры кривой.

Уравнение (5.1) называют выборочным уравнением регрессии. При правильно определенной аппроксимирующей функции с увеличением объема выборки она все надежнее описывает уравнение регрессии.

Для установления наличия корреляционной связи и вида уравнения регрессии в случае парной корреляции зависимость изображают графически в виде точек на координатной плоскости. Это изображение статистической зависимости называют диаграммой рассеивания или полем корреляции.

По расположению эмпирических точек выбирают вид регрессионной зависимости. Чаще всего выбирается линейное уравнение регрессии, которое имеет вид:

(5.2)

В уравнении регрессии используются и другие типы функций:

1) параболическая – ;

2) гиперболическая – ;

3) показательная – и др.

Неизвестные параметры выбираются методом наименьших квадратов (МНК), то есть так, чтобы сумма квадратов отклонений эмпирических значений от значений , найденных по уравнению регрессии, была минимальной. Например, для линейной функции:

(5.3)

На основании необходимого условия экстремума функции двух переменных приравниваем к нулю ее частные производные:

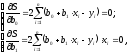
откуда после преобразований получим систему нормальных уравнений для определения параметров линейной регрессии:

(5.4)

Разделив обе части уравнений (5.4) на , получим:

(5.5)

где средние определяются по формулам:

(5.6) (5.7)

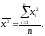(5.8) (5.9)

Подставляя значение

(5.10)

из первого уравнения системы (5.5) в уравнение регрессии (5.2) получим

. (5.11)

Коэффициент называется коэффициентом регрессии по . Он показывает на сколько единиц в среднем изменяется переменная при увеличении переменной на одну единицу.

Решая систему (5.5), найдем

(5.12)

где выборочная дисперсия переменной :

(5.13)

выборочная ковариация:

. (5.14)

Для оценки влияния факторного признака на результативную переменную может рассчитываться коэффициент эластичности в среднем для всей совокупности:

. (5.15)

Коэффициент эластичности показывает на сколько процентов в среднем изменится результативная переменная при изменении фактора на 1%.

Пример 5.1. Экспериментальные данные, характеризующие зависимость между сменной добычей угля на одного рабочего (т) и мощностью пласта (м), по шахтам приведены в Таблице 5.1. Найти уравнение регрессии по . Таблица 5.1 1 2 3 4 5 6 7 8 9 10 6 11 13 10 6 7 9 8 8 12 90 4 10 10 8 6 4 9 7 5 11 74 36 121 169 100 36 49 81 64 64 144 864 16 100 100 64 36 16 81 49 25 121 608 24 110 130 80 36 28 81 56 40 132 717 Изобразим полученную зависимость графически (рис. 5.1). Рис. 5.1. По расположению точек можно предполагать линейную зависимость между переменными и По формулам (5.6)-(5.14) находим выборочные характеристики и параметры уравнения регрессии: Уравнение регрессии по или . Из уравнения следует, что при увеличении мощности пласта на 1 метр добыча угля на одного рабочего увеличивается в среднем на 0,944 тонн. По формуле (5.15) определяем коэффициент эластичности: , который показывает, что при увеличении мощности пласта на 1% добыча угля на одного рабочего увеличивается в среднем на 1,216%.