
- •Статистика Учебное пособие.
- •Содержание (часть 1)
- •Глава 1. Методология и основные понятия статистики.
- •Основные понятия статистики.
- •1.2. Статистическое наблюдение.
- •1.3. Сводка и группировка статистических данных.
- •1.4. Представление статистических данных.
- •1.4.1. Статистические таблицы.
- •1.4.2. Графическое изображение статистических данных.
- •1.4.3. Решение типовых задач.
- •Глава 2. Статистические показатели.
- •2.1. Абсолютные величины.
- •2.2. Относительные величины.
- •2.3. Средние величины.
- •2.3.1. Структурные средние.
- •2.3.2. Степенные средние.
- •Глава 3. Показатели вариации.
- •3.1. Абсолютные и относительные показатели.
- •3.3. Показатели конкуренции.
- •Глава 4. Выборочное наблюдение.
- •4.1. Выборочная совокупность (выборка) и способы её отбора.
- •4.2. Оценка математического ожидания (средней величины).
- •4.3. Оценка вероятности или доли элементов генеральной совокупности, обладающих определенным признаком.
- •Глава 5. Корреляционная связь и ее анализ.
- •5.1. Корреляционно-регрессионный анализ.
- •5.1.1. Уравнение регрессии.
- •5.1.2. Коэффициент корреляции.
- •5.1.3. Оценка уравнения регрессии.
- •5.2. Непараметрические показатели связи.
- •5.2.1. Коэффициенты ранговой корреляции.
- •5.2.2. Анализ связи атрибутивных признаков.
- •5.2.3. Анализ связи альтернативных признаков.
- •Глава 6. Статистическое изучение динамики.
- •6.1. Виды рядов динамики. Средний уровень ряда динамики.
- •6.3. Выявление основной тенденции ряда динамики.
- •6.4. Сезонные колебания.
- •Глава 7. Экономические индексы.
- •7.1. Виды экономических индексов.
- •7.2. Общие индексы средних величин.
- •Глава 8. Экспертное оценивание.
- •8.1. Организация экспертизы.
- •8.2. Обработка и анализ результатов экспертизы.
- •8.2.1. Ранжирование объектов.
- •8.2.2. Оценивание по балльной шкале.
- •8.2.3. Парные сравнения.
4.2. Оценка математического ожидания (средней величины).
Пусть распределение значений
количественного признака в большой
выборке ( )
известно и записано в табличной форме:
)
известно и записано в табличной форме:
|
Значение,
|
Частота,
|
|
…
|
…
|
|
Итого |
|
Выборочные среднее и дисперсия рассчитываются по формулам:
 (4.1)
(4.1)
 (4.2)
(4.2)
Величины
 и
и
 являются оценками параметров генеральной
совокупности: математического ожидания
являются оценками параметров генеральной
совокупности: математического ожидания
 и дисперсии
и дисперсии
 .
Оценка
.
Оценка
 является случайной величиной,
распределенной по нормальному закону.
Величина
является случайной величиной,
распределенной по нормальному закону.
Величина
 является центрированной (математическое
ожидание равно нулю) и нормированной
(дисперсия равна 1), поэтому для нахождения
квантилей распределения
является центрированной (математическое
ожидание равно нулю) и нормированной
(дисперсия равна 1), поэтому для нахождения
квантилей распределения
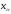 можно использовать таблицы функции
распределения стандартного нормального
распределения.
можно использовать таблицы функции
распределения стандартного нормального
распределения.
Истинное значение параметра
 можно оценить при помощи доверительного
интервала, который его включает
можно оценить при помощи доверительного
интервала, который его включает
 ,
(4.3)
,
(4.3)
где
 доверительная
вероятность (надежность оценки), а
доверительная
вероятность (надежность оценки), а
 уровень
значимости, то есть вероятность ошибки.
уровень
значимости, то есть вероятность ошибки.
Величина предельной ошибки равна:
-
повторная выборка
 ,
(4.4)
,
(4.4)
-
бесповторная выборка

 .
(4.5)
.
(4.5)
Если объем генеральной совокупности существенно больше объема выборки, либо неизвестен, то пользуются формулой (4.4).
Средние ошибки выборки находят по формулам
 и
и
 . (4.6)
. (4.6)
Интервал может быть двусторонним, либо односторонним.
|
Пример 4.1. Произведены измерения признака, распределенного на элементах генеральной совокупности неизвестного объема. Результаты измерений и вычислений приведены в таблице. № п/п
1 6 5 30 1,98 3,92 19,6 2 7 10
0 0,98 0,96 9,6 3 8 20 160 0,02 0,0004 0,008 4 9 11 99 1,02 1,04 11,44 5 10 4 40 2,02 4,08 16,32 Итого
50 399
56,968 Точечные оценки находим по формулам (4.1) и (4.2).
По таблице нормального распределения
(Приложение 1) находим
По формуле
(4.4) найдем
Следовательно,
Проводим те
же вычисления и находим:
Так как
интервал двусторонний, квантиль
распределения находим для
По формуле
(4.4) найдем
Вычисляем
левую и правую границы интервала:
Получили:
|
Если
объем выборки небольшой
 ,
то методика расчета доверительных
интервалов немного изменяется. Для
сгруппированных данных выборочное
среднее определяем, как и ранее (4.1), а
дисперсию по формуле:
,
то методика расчета доверительных
интервалов немного изменяется. Для
сгруппированных данных выборочное
среднее определяем, как и ранее (4.1), а
дисперсию по формуле:
 .
(4.7)
.
(4.7)
Для не сгруппированных данных используем формулы:
 (4.8)
(4.8)
 .
(4.9)
.
(4.9)
Величина
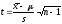 описывается стандартным
описывается стандартным
 распределением
Стьюдента с
распределением
Стьюдента с
 степенями свободы, поэтому для нахождения
квантилей распределения
степенями свободы, поэтому для нахождения
квантилей распределения
 используют таблицы
используют таблицы
 распределения
(Приложение 2).
распределения
(Приложение 2).
Предельная ошибка для повторной выборки будет равна

 .
(4.10)
.
(4.10)
|
Пример 4.2. Произведены измерения признака, распределенного на элементах генеральной совокупности неизвестного объема. Результаты измерений и вычислений приведены в таблице. По формулам (4.1) и (4.7) получаем точечные оценки.
По таблице
степеней свободы
По формуле (4.10) найдем
Следовательно,
Находим:
Для
двусторонней критической области,
квантиль распределения
По
формуле (4.10) найдем
Вычисляем
левую и правую границы интервала:
Получили:
|
Если задана предельная ошибка и
доверительная вероятность, из формул
(4.4) и (4.10) можно найти необходимое
количество измерений (объем выборки).
Например, из (4.4) при заданных
 находим:
находим:
 (4.11)
(4.11)
|
Пример 4.3. В условиях
Примера 4.1 определить необходимое
число измерений, если
|














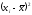

 ;
;
 ;
;
 .
. .
. .
. .
.

 с вероятностью 0,95 .
с вероятностью 0,95 . .
. с вероятностью 0,95 .
с вероятностью 0,95 . .
. :
:
 .
. .
.
 ;
;
 .
. с вероятностью 0,95 .
с вероятностью 0,95 .






 ;
;
 ;
;
 .
.
 .
. распределения
(Приложение 2) для односторонней
критической области и числа
распределения
(Приложение 2) для односторонней
критической области и числа находим
находим
 .
.
 .
.

 с вероятностью 0,95 .
с вероятностью 0,95 . .
. с вероятностью 0,95 .
с вероятностью 0,95 . .
. .
. .
.
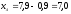 ;
;
 .
. с вероятностью 0,95 .
с вероятностью 0,95 .
 и
и
 .
Из таблиц (Приложение 1) для двустороннего
интервала находим
.
Из таблиц (Приложение 1) для двустороннего
интервала находим
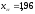 .
По формуле (4.11) получаем
.
По формуле (4.11) получаем
 ; то есть
; то есть
 .
.