Тема 4 «Ряды динамики»

Задание 4.1.

На основе данных годовых отчетов с.-х. предприятия (организаций) области исчислите: показатели ряда динамики с постоянной и переменной базой сравнения:

1. Абсолютный прирост, темп прироста;

2. Среднегодовой абсолютный прирост за 200. – 200. гг. И среднегодовой темп роста урожайности за 200. – 200. гг.

3. Изобразите ряд динамики урожайности графически и сделайте анализ исчисленных показателей.

Методические указания

Показатели, характеризующие динамику общественных явлений (в данном примере урожайности), вычисляются следующим образом:

Абсолютный прирост () исчисляется как разность между уровнями (У) ряда динамики:

базисный

цепной где

- абсолютный прирост

- уровень, который сравнивается; последующий

- уровень, с которым производится сравнение, базисный

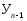- уровень предыдущего периода

Темп роста (Т_р) рассчитывается как отношение сравниваемого уровня и уровня, принятого за базу сравнения:

Базисный

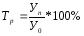
Цепной

Темп прироста (Тпр) вычисляется как отношение абсолютного прироста к уровню ряда динамики, принятому за базу сравнения:

Базисный Цепной

Или

Темп прироста можно рассчитать также путем вычитания из темпа роста 100%.

1. Исчисленные показатели ряда динамики урожайности необходимо оформить в следующую таблицу 4.1.

Таблица 4.1.

Ряд динамики и показатели, его характеризующие

Годы	Уровни ряда динамики	Абсолютный прирост, ц/га			Темп роста, %			Темп прироста, %
		базисный	цепной	базисный		цепной	базисный		цепной
	У
1992 1993 1994 1995 1996 1997 1998 1999 2000 2001

2. Среднегодовой абсолютный прирост определяется по следующей формуле:

или где

- конечный уровень ряда динамики (2001 г.)

- начальный уровень ряда динамики (1992г.)

- число уровней ряда динамики

- цепной

- число абсолютного прироста

Среднегодовой темп прироста определяется по формуле:

где - среднегодовой темп роста

- уровень урожайности 2001 г.

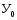- уровень урожайности 1992 г.

- число уровней ряда динамики

или по формуле:

где и т.д. – годовые темпы роста (цепные)

- число темпов роста

Выводы:

Задание 4.2.

Произвести сглаживание скользящей средней по 3-х летиям ряда динамики урожайности зерновых культур по с.х. предприятиям (организациям) Тюменской области (по заданию 4.1., таблица 4.1.)

, ; и т.д.

Задание 4.3.

Произвести аналитическое выравнивание динамического ряда урожайности зерновых культур (по заданию 4.1., таблица 4.1.)

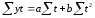
при

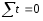
Подставить «а» и «b» в исходное уравнение и выровнять динамический ряд, расчетные данные занести в таблицу 4.3.

Выводы:

Таблица 4.3.

К анализу динамического ряда урожайности зерновых культур

Годы	Уровни ряда	Аналитическое выравнивание					Годовой темп роста
	У	t	T2	tу
1992 1993 1994 1995 1996 1997 1998 1999 2000
Итого

Изобразить на графике фактический и выровненный ряды урожайности зерновых. Сделать выводы.

Задание 4.4.

Определить показатели сезонности производства молока. Сезонность производства охарактеризовать при помощи графика (таблица 4.4.).

Таблица 4.4.

Производство молока в с.-х. предприятиях Тюменской области

Месяцы	Валовой надой, ц	Показатели сезонности, %
Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь	630 690 611 822 988 1348 985 981 758 601 558 540

,

, где

- ежемесячные уровни ряда производства молока

Выводы: