
- •Оглавление
- •Тема: методы анализа переходных процессов в линейных цепях
- •Переходные процессы в линейных цепях
- •Метод решения линейных дифференциальных уравнений
- •Включение цепи r, c на постоянное напряжение
- •Разряд конденсатора на активное сопротивление
- •Включение цепи r, l на постоянное напряжение
- •Разряд конденсатора в цепиL,c,r.
- •Воздействие постоянного напряжения на l,c,r цепь
- •Воздействие гармонической э.Д.С, на колебательный контур
- •Спектральный метод анализа переходных процессов
- •Нахождение токов и напряжений в цепях с помощью преобразований Фурье
- •Свойства цепи r, с
- •Свойства цепи r, l
- •Условия неискаженной передачи сигнала
- •Применение преобразования Лапласа при расчете переходных процессов
- •Преобразование Лапласа
- •Основные свойства преобразования Лапласа
- •Расчет переходных процессов с помощью преобразования Лапласа.
- •Временной метод анализа Дюамеля
- •Переходные характеристики цепи
- •Интеграл Дюамеля и его применение
- •Импульсная характеристика цепи
- •Связь временных и частотных характеристик цепи
Применение преобразования Лапласа при расчете переходных процессов
Преобразование Лапласа
Спектральный метод анализа позволяет уяснить физические процессы в цепях и в ряде случаев сравнительно прост. Но в некоторых случаях вычисление интеграла Фурье оказывается затруднительным. Кроме того, спектральный метод не является универсальным. Действительно, преобразование Фурье применимо лишь к абсолютно интегрируемым функциям, т.е. удовлетворяющим условию
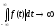 . (4.1)
. (4.1)
Возникают затруднения и при использовании обычного вида этого метода для решения задач, в которых начальные условия отличны от нуля, т.е. когда цель имеет начальный запас энергии.
Спектральный
метод становится более универсальными
нахождение обратного преобразования
Фурье облегчается, если интеграл Фурье
распространить на комплексное переменное,
т.е. если перейти от вещественного
переменного
 к комплексному переменному
к комплексному переменному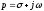 .
.
Пусть
функция
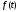 задана для положительных значений
задана для положительных значений и равна нулю при
и равна нулю при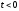 ,
причем она может не удовлетворять
условию (4.1). Умножая
,
причем она может не удовлетворять
условию (4.1). Умножая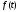 на
на
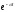 ,
где
,
где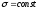 и
и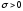 ,
получим, пользуясь выражением (3.1):
,
получим, пользуясь выражением (3.1):
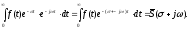 (4.2)
(4.2)
На основании (3.2) тогда имеем
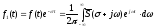 .
.
Отсюда видно, что
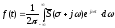 (4.3)
(4.3)
Вводя
комплексную переменную
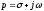 ,
запишем вместо (4.2)
,
запишем вместо (4.2)
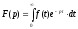 . (4.4)
. (4.4)
Полученное
соотношение, преобразующее вещественную
функцию
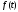 вещественного переменного
вещественного переменного в функцию
в функцию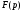 комплексного переменного
комплексного переменного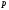 ,
называется преобразованием Лапласа.
Функцию
,
называется преобразованием Лапласа.
Функцию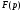 называют
изображением функции
называют
изображением функции
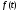 ,
а
саму функцию
,
а
саму функцию
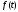 называют
оригиналом. Символически связь между
изображением и оригиналом записывается
так:
называют
оригиналом. Символически связь между
изображением и оригиналом записывается
так:
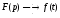
Из
изложенного следует, что изображение
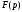 может
быть формально получено из прямого
преобразования Фурье заменой
может
быть формально получено из прямого
преобразования Фурье заменой
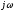 комплексным переменным
комплексным переменным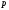 .
Функция
.
Функция
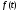 имеет
изображение, если
имеет
изображение, если
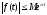 ,
где
,
где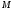 и
и - постоянные числа. В качестве примера
функции, не имеющей изображения, можно
привести
- постоянные числа. В качестве примера
функции, не имеющей изображения, можно
привести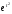 или
или
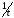 .
Функции, встречающиеся в радиотехнике,
обычно имеют изображение.
.
Функции, встречающиеся в радиотехнике,
обычно имеют изображение.
Теперь
в ином виде представим выражение (4.3),
переходя к переменной
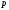 ,
Так
как
,
Так
как
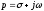 ,
то
,
то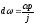 ,a
пределы интегрирования в (4.3) при
изменении
,a
пределы интегрирования в (4.3) при
изменении
 от
от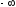 до
до теперь будут соответственно
теперь будут соответственно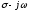 и
и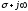 .Тогда
получаем:
.Тогда
получаем:
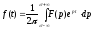 . (4.5)
. (4.5)
Это соотношение, которое известно в математике как формула обращения Римана-Моллина, иногда называют обратным преобразованием Лапласа.
В
отличие от интеграла Фурье, где функция
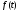 представлена суммой бесконечно большого
числа элементарных гармонических
колебаний, здесь функция
представлена суммой бесконечно большого
числа элементарных гармонических
колебаний, здесь функция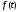 представлена суммой бесконечно большого
числа элементарных колебаний, убывающих
по экспоненциальному закону.
представлена суммой бесконечно большого
числа элементарных колебаний, убывающих
по экспоненциальному закону.
В
выражении (4.5) интегрирование ведется
по прямой, лежащей на плоскости
комплексного переменного
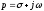 и отстоящей от оси мнимой величины
и отстоящей от оси мнимой величины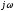 на расстоянии
на расстоянии .
В теории функций комплексного переменного*)доказывается, что интегрирование в
выражении (4.5) может быть произведено
по замкнутому контуру (рис. 4.1). Контур
интегрирования должен охватывать все
полюсы подинтегралыюй функции, т.е.
точки
.
В теории функций комплексного переменного*)доказывается, что интегрирование в
выражении (4.5) может быть произведено
по замкнутому контуру (рис. 4.1). Контур
интегрирования должен охватывать все
полюсы подинтегралыюй функции, т.е.
точки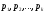 плоскости комплексного переменного,
в которых подинтегральная функция
выражения (4.5) обращается в бесконечность.
Вычисление интеграла при этом сводится
к определению суммы вычетов (обозначаемых
буквами
плоскости комплексного переменного,
в которых подинтегральная функция
выражения (4.5) обращается в бесконечность.
Вычисление интеграла при этом сводится
к определению суммы вычетов (обозначаемых
буквами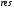 )
подинтегральной
функции в полюсе, т.е.
)
подинтегральной
функции в полюсе, т.е.
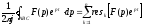 (4.6)
(4.6)
При вычислении вычетов подинтегральную функцию во многих случаях можно представить в виде отношения двух функций:
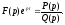
Значения
комплексного переменного
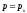 ,
при которых знаменатель
,
при которых знаменатель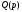 обращается
в нуль, а следовательно, подинтегральная
функция — в бесконечность, и будут
полюсами под интегральной функции. В
данном случае полюсы являются корнями
уравнения
обращается
в нуль, а следовательно, подинтегральная
функция — в бесконечность, и будут
полюсами под интегральной функции. В
данном случае полюсы являются корнями
уравнения
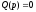 .
Число
полюсов подинтегральной функции
определяется числом корней этого
уравнения.
.
Число
полюсов подинтегральной функции
определяется числом корней этого
уравнения.
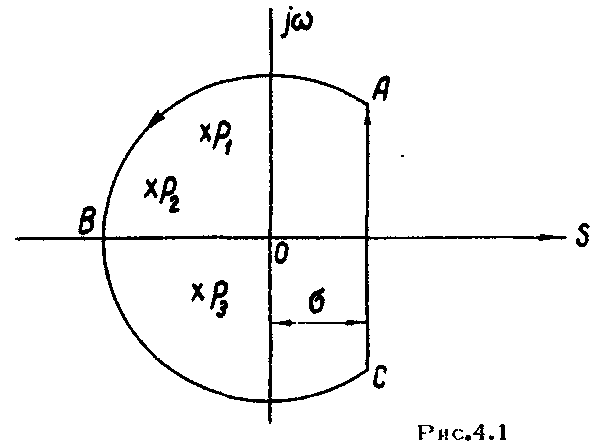
Пусть
число полюсов равно
 .
Каждый
из них может иметь различный порядок,
обозначаемый через
.
Каждый
из них может иметь различный порядок,
обозначаемый через
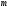 .
Порядок
.
Порядок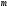 полюса
полюса
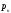 равен
порядку младшей отличной от нуля
производной функции
равен
порядку младшей отличной от нуля
производной функции
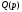 по
по
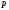 при
при
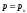 ,
т.е. порядку производной
,
т.е. порядку производной
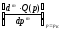
Вычет
подинтегралъной функции в полюсе
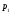 порядка
порядка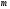 находится по формуле
находится по формуле
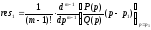
Если
полюс
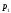 простой,
т.е. первого порядка, то вычет в этом
полюсе определяется выражением
простой,
т.е. первого порядка, то вычет в этом
полюсе определяется выражением
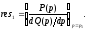 (4.8)
(4.8)
Для
пояснения изложенного рассмотрим
простейшие примеры. Пусть задана
единичная функция
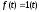 .
Изображение
этой функции будет
.
Изображение
этой функции будет
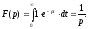
Тогда оригинал по этому изображению находится с помощью (4.5)
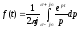
или,
так как полюс подинтегральной функции
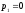 ,
то
согласно (4.8) вычет подинтегральной
функции в этом полюсе
,
то
согласно (4.8) вычет подинтегральной
функции в этом полюсе
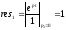
и
на основании (4.6) имеем
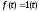 ,
т.е. получаем исходную функцию. Символически
можно записать:
,
т.е. получаем исходную функцию. Символически
можно записать:
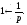 (4.9)
(4.9)
Пусть теперь задана экспоненциальная функция
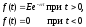
Изображение этой функции:
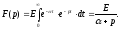
По найденному изображению определим теперь оригинал
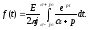
Полюсом
подинтегральной функции является
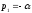 .
Вычет
в этом полюсе равен
.
Вычет
в этом полюсе равен
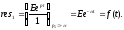
Таким образом, можем записать:
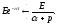 (4.10)
(4.10)
Легко
убедиться, что если задана функция
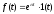 ,
то оказывается справедливой запись
,
то оказывается справедливой запись
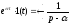 . (4.11)
. (4.11)
Для
дельта функции
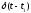 изображение имеет вид:
изображение имеет вид:
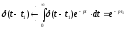 . (4.12)
. (4.12)
Для
вычисления оригиналa
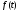 по
известному изображению кроме рассмотренного
способа вычетов в ряде случаев удобно
применять так называемую теорему
разложения, предложенную Хевисайдом.
по
известному изображению кроме рассмотренного
способа вычетов в ряде случаев удобно
применять так называемую теорему
разложения, предложенную Хевисайдом.
Пусть
изображение
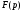 является
рациональной дробью
является
рациональной дробью
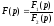 ,
,
представляемой
через полиномы
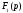 и
и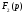 ,
причем
степень
,
причем
степень
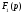 меньше
степени
меньше
степени
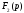 .
Тогда
можно показать, что если уравнение
.
Тогда
можно показать, что если уравнение
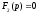 имеет
имеет различных корней, то функция
различных корней, то функция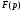 представляется следующей суммой:
представляется следующей суммой:
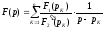 . (4.13)
. (4.13)
Находя
по формуле (4.11) оригинал функции
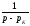 ,
получим выражение для нахождения по
изображению
,
получим выражение для нахождения по
изображению
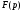 оригинала,
т.е. функции
оригинала,
т.е. функции
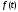 :
:
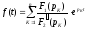 . (4.14)
. (4.14)
Это
выражение, являющееся записью теоремы
разложения, позволяет представить
искомую функцию
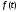 в виде совокупности
в виде совокупности экспоненциальных функций. При этом
предполагается, что функция
экспоненциальных функций. При этом
предполагается, что функция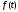 тождественно
равна нулю при
тождественно
равна нулю при
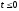 .
.
Выражению
(4.14) можно придать иной вид для случая,
если один из корней уравнения
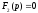 равен нулю. Обозначим
равен нулю. Обозначим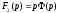 ,
где
,
где
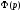 -полином,
не имеющий нулевых корней. Выделим в
выражении (4.13) слагаемое, соответствуют
ее нулевому корню. Так как в принятом
обозначении для производной функции
-полином,
не имеющий нулевых корней. Выделим в
выражении (4.13) слагаемое, соответствуют
ее нулевому корню. Так как в принятом
обозначении для производной функции
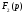 имеем
имеем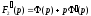 ,
то
вместо
(4.13) получаем:
,
то
вместо
(4.13) получаем:
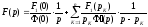 .
.
Учитывая
выражения (4.9) и (4.11), получаем для
нахождения оригинала
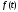 по заданному изображению
по заданному изображению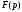 выражение
выражение
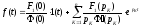 ,
(4.15)
,
(4.15)
где
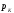 -
корни уравнения
-
корни уравнения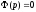 .
Если
полином
.
Если
полином
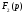 имеет кратные корни, формула для
нахождения
имеет кратные корни, формула для
нахождения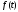 значительно усложняется и ее рассматривать
не будем.
значительно усложняется и ее рассматривать
не будем.
