
- •Оглавление
- •Тема: методы анализа переходных процессов в линейных цепях
- •Переходные процессы в линейных цепях
- •Метод решения линейных дифференциальных уравнений
- •Включение цепи r, c на постоянное напряжение
- •Разряд конденсатора на активное сопротивление
- •Включение цепи r, l на постоянное напряжение
- •Разряд конденсатора в цепиL,c,r.
- •Воздействие постоянного напряжения на l,c,r цепь
- •Воздействие гармонической э.Д.С, на колебательный контур
- •Спектральный метод анализа переходных процессов
- •Нахождение токов и напряжений в цепях с помощью преобразований Фурье
- •Свойства цепи r, с
- •Свойства цепи r, l
- •Условия неискаженной передачи сигнала
- •Применение преобразования Лапласа при расчете переходных процессов
- •Преобразование Лапласа
- •Основные свойства преобразования Лапласа
- •Расчет переходных процессов с помощью преобразования Лапласа.
- •Временной метод анализа Дюамеля
- •Переходные характеристики цепи
- •Интеграл Дюамеля и его применение
- •Импульсная характеристика цепи
- •Связь временных и частотных характеристик цепи
Интеграл Дюамеля и его применение
Вычисление отклика цепи при воздействии на него сигнала любой формы упрощается, если воспользоваться интегралом Дюамеля, выражение которого можно получить, применяя принцип суперпозиции.
Пусть
внешнее воздействие, форма которого
доказана на рис. 5.5, задано функцией ,
являющейся, как и ее производная,
непрерывной. При
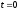 функция имеет значение
функция имеет значение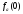 .
Представим эту функцию в виде
.
Представим эту функцию в виде элементарных перепадов. Для этого ось
абсцисс разобьем на
элементарных перепадов. Для этого ось
абсцисс разобьем на равных
интервалов величиной
равных
интервалов величиной
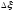 и построим
и построим элементарных
перепадов, появляющихся в моменты
элементарных
перепадов, появляющихся в моменты
 .
Величина перепада
.
Величина перепада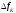 зависит от момента
зависит от момента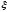 его появления. Подобное представление
будет точнее, если
его появления. Подобное представление
будет точнее, если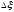 становится
бесконечно малой, т.е. если
становится
бесконечно малой, т.е. если
 ,
а число
элементарных перепадов растет до
бесконечности. Тогда величина элементарного
перепада становится равной
,
а число
элементарных перепадов растет до
бесконечности. Тогда величина элементарного
перепада становится равной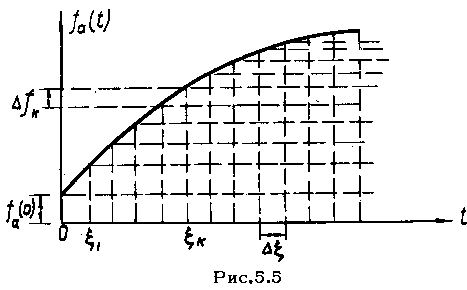
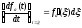 .
.
Отклик
цени на такое элементарное воздействие
равен
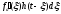 .
Результирующий отклик цепи на воздействие
всех элементарных перепадов, появляющихся
в интервале времени от
.
Результирующий отклик цепи на воздействие
всех элементарных перепадов, появляющихся
в интервале времени от до
до ,
равен сумме откликов от воздействия
каждого из них. Полагая, что каждый
элементарный перепад, за исключенном
начального, бесконечно мал, получим для
результирующего отклика выражение
,
равен сумме откликов от воздействия
каждого из них. Полагая, что каждый
элементарный перепад, за исключенном
начального, бесконечно мал, получим для
результирующего отклика выражение
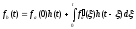 . (5.7)
. (5.7)
С помощью этого соотношения, называемого интегралом Дюамеля, удобно по известной переходной характеристике цепи вычислять отклик на воздействие любой формы. Соотношение (5.7) можно записать в другой форме. Интегрируя по частям второе слагаемое (5.7), имеем:
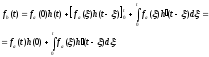 (5.8)
(5.8)
Иногда
удобно воспользоваться иным видом
записи интеграла Дюамеля. Получим этот
вид, эаменив в соотношении (5.7) переменное,
т.е. положив
 .Тогда
.Тогда ,
а пределы интегрирования будут теперь
от
,
а пределы интегрирования будут теперь
от до
0. Однако, если изменить знак перед
интегралом, то вновь получаем пределы
интегрирования от 0 до
до
0. Однако, если изменить знак перед
интегралом, то вновь получаем пределы
интегрирования от 0 до
 т.е.
находим
т.е.
находим
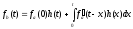
Заменяя
в этом выражении
 через
через ,
получим окончательно:
,
получим окончательно:
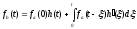 . (5.9)
. (5.9)
Интегрируя по частям второе слагаемое выражения (5.9), получим четвертый вид записи интеграла Дюамеля:
 . (5.10)
. (5.10)
В
качестве примера применения интеграла
Дюамеля найдем отклик дифференцирующей
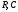 цепи (рис.3.1а) на воздействие перепада
напряжения
цепи (рис.3.1а) на воздействие перепада
напряжения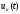 ,
имеющего линейно-нарастающий фронт
(рис 5.6а). 3ная коэффициент передачи цепи,
заданный выражением (3.10) и спектральную
функцию единичного перепада
,
имеющего линейно-нарастающий фронт
(рис 5.6а). 3ная коэффициент передачи цепи,
заданный выражением (3.10) и спектральную
функцию единичного перепада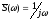 ,
находим с помощью спектрального метода
переходную характеристику дифференцирующей
цепи:
,
находим с помощью спектрального метода
переходную характеристику дифференцирующей
цепи:
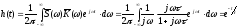 ,
,
при
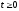 (5.11)
(5.11)
Входное
напряжение в соответствии с (5.6) можно
представить в виде двух функций
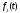 и
и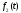 .
Отклик цепи на воздействие функции
.
Отклик цепи на воздействие функции найдем с помощью интеграла Дюамеля по
формуле (5.8):
найдем с помощью интеграла Дюамеля по
формуле (5.8):
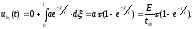
Тогда
отклик цепи на воздействие функции
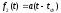 определяется выражением
определяется выражением
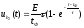 при
при
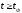 .
.
Результирующий
отклик на напряжение
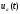 ,
согласно (5.1) равный
,
согласно (5.1) равный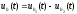 ,
показан на рис.5.6в.
,
показан на рис.5.6в.
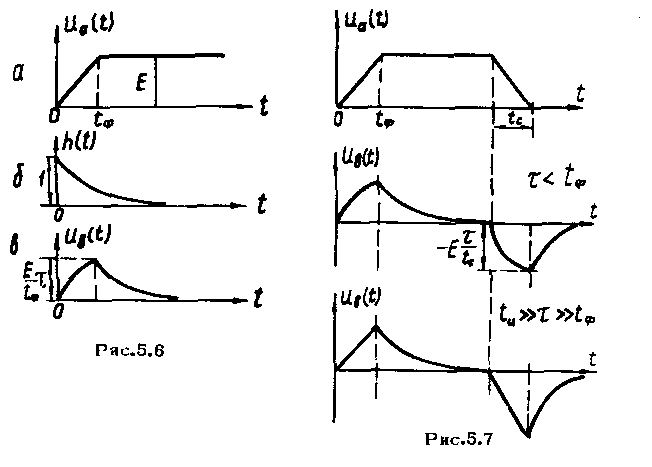
Полученный
результат и принцип суперпозиции
позволяют построить график напряжения
на выходе дифференцирующей цепи при
подаче на ее вход импульса трапецеидальной
формы (рис.5.7а). Если выполняется
неравенство
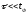 ,
то за время нарастания входного
напряжения конденсатор
,
то за время нарастания входного
напряжения конденсатор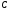 успевает
заметно зарядиться и на нем оказывается
часть полного напряжения источника. На
сопротивлении
успевает
заметно зарядиться и на нем оказывается
часть полного напряжения источника. На
сопротивлении при этом напряжение нарастает по закону,
отличающемуся от линейного (рис.5.7б),
достигая максимальной величины, равной
при этом напряжение нарастает по закону,
отличающемуся от линейного (рис.5.7б),
достигая максимальной величины, равной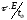 .
Если
же
.
Если
же
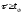 ,то
за время
,то
за время конденсатор
заряжается очень мало и напряжение на
сопротивлении
конденсатор
заряжается очень мало и напряжение на
сопротивлении
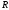 в течение этого времени изменяется
практически по линейному закону, т.е.
фронт выходного импульса близок но
форме к фронту входного (рис.5.7в).
в течение этого времени изменяется
практически по линейному закону, т.е.
фронт выходного импульса близок но
форме к фронту входного (рис.5.7в).
