
Лекция 2
(6 часов)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Математический аппарат при анализе непрерывных САР.
Понятие оператора
Простейшим математическим понятием является число, выражающее количественно величину параметра либо воздействия.
 Более
широким понятием является числовая
ось, на которой расположено бесконечное
множество чисел (рис.2.1). На отрезкахABиA1B1также
расположено бесконечное число точек.
В таких случаях говорят, что множествоABширемножестваA1B1.
Сами эти множества, закон пересчета
чисел которых неизвестен, называютконтинуальными. Когда удается
указать закон пересчета чисел, множество
называютсчетным. Если все точки
множества можно пересчитать, то множество
называютконечным.
Более
широким понятием является числовая
ось, на которой расположено бесконечное
множество чисел (рис.2.1). На отрезкахABиA1B1также
расположено бесконечное число точек.
В таких случаях говорят, что множествоABширемножестваA1B1.
Сами эти множества, закон пересчета
чисел которых неизвестен, называютконтинуальными. Когда удается
указать закон пересчета чисел, множество
называютсчетным. Если все точки
множества можно пересчитать, то множество
называютконечным.
На практике инженерам приходится иметь дело именно с континуальными множествами чисел, которые могут отражать диапазон изменения некоторого воздействия (управляющего или возмущающего) или какого-либо параметра.
 Уточним
понятие функции. Функцией
называется всякое соответствие между
точками одного множества и точками
другого множества (каждой точке одного
множества соответствует точка другого
множества). Например (рис.2.2а), если заданы
множества чисел
Уточним
понятие функции. Функцией
называется всякое соответствие между
точками одного множества и точками
другого множества (каждой точке одного
множества соответствует точка другого
множества). Например (рис.2.2а), если заданы
множества чисел
![]() и
и![]() ,
и функция
,
и функция![]() ,
то в этом случае говорят, что функцияf
определена (задана) на множестве U
со значениями на множестве X.
,
то в этом случае говорят, что функцияf
определена (задана) на множестве U
со значениями на множестве X.
Функция в инженерном сознании ассоциируется с безынерционными звеньями (рис.2.2б), реализующими требуемую функциональную зависимость.
Функционалом называется всякое соответствие между функциями одного множества и точками другого множества (каждой функции соответствует точка). Функционалы задаются на множестве функций. Типичный пример функционала:
![]() ,
,
где
f(x)
– некоторая заданная функция;
![]() – варьируемое количество элементарных
участков интегрирования.
– варьируемое количество элементарных
участков интегрирования.
Другой
пример – если известна функция двух
переменных
![]() ,
то можно построить функционалы типа
,
то можно построить функционалы типа
![]()
при
разных значениях аргумента x
и фиксированном
![]() .
.
В ТАУ функционалы используются при построении оптимальных САУ для определения требуемого соотношения между параметрами САР.
 Всякое
соответствие между функциями одного
множества (X)
и функциями другого множества (Y)
называется оператором.
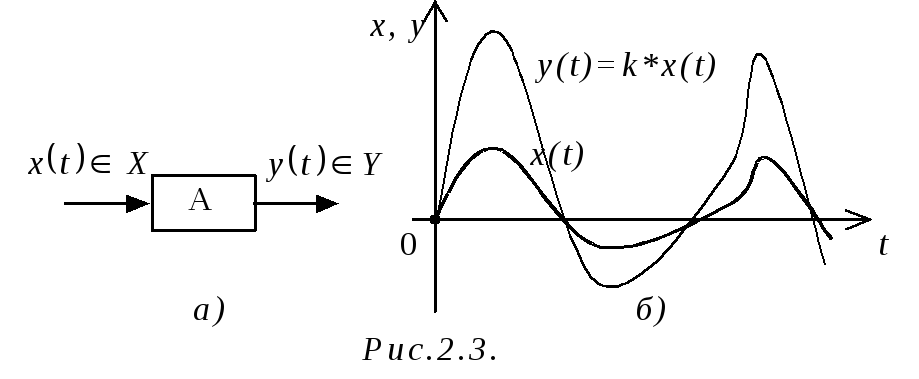
Например (рис.2.3а), пусть A – оператор,
отражающий коэффициент передачи
(усиления) некоторого устройства (
Всякое
соответствие между функциями одного
множества (X)
и функциями другого множества (Y)
называется оператором.
Например (рис.2.3а), пусть A – оператор,
отражающий коэффициент передачи
(усиления) некоторого устройства (![]() ).
Тогда оператор A связывает все входные
функцииx(t)
с выходными y(t),
воздействуя на входной сигнал (в нашем
примере – умножая его в каждый момент
времени на коэффициент k
– усиливая его). Такое звено в результате
формирует выходную функцию y(t),
отличающуюся от входной x(t)
на постоянный множитель (рис.2.3б).
).
Тогда оператор A связывает все входные
функцииx(t)
с выходными y(t),
воздействуя на входной сигнал (в нашем
примере – умножая его в каждый момент
времени на коэффициент k
– усиливая его). Такое звено в результате
формирует выходную функцию y(t),
отличающуюся от входной x(t)
на постоянный множитель (рис.2.3б).
Понятие оператора широко используется в ТАУ. Наиболее широко используемыми являются операторы дифференцирования и интегрирования (определения неопределенного интеграла).
В частности, если оператор
A=TD,
где
![]() – символ (оператор) дифференцирования
по времени,T
– некоторая постоянная времени [c], то
воздействие оператора на некоторую
входную функцию x(t)
дает выходную функцию
– символ (оператор) дифференцирования
по времени,T
– некоторая постоянная времени [c], то
воздействие оператора на некоторую
входную функцию x(t)
дает выходную функцию
![]() .
.
То есть, результатом использования оператора TD есть то, что он, воздействуя на входной сигнал x(t), выдает производную от этого сигнала по времени в каждый момент t, помноженную на коэффициент T (рис.2.4).
Обратный
оператор
![]() соответствует интегрированию. Например,
если
соответствует интегрированию. Например,
если
![]() ,
,
 то
выходной сигнал
то
выходной сигнал
![]() .
.
Результатом использования оператора интегрирования есть то, что он, воздействуя на входной сигнал x(t), выдает для каждого нового значения t, новое значение площади. Геометрический смысл оператора интегрирования понятен из рис.2.4.
Таким образом, если оператор дифференцирования "проникает" внутрь сигнала, в его отдельные точки, то оператор интегрирования выдает самые обобщенные представления о входном сигнале.
Более сложными операторами, используемыми в ТАУ, являются операторы-полиномы (многочлены) вида
![]() .
.
Их называют еще дифференциальными операторами. Смысл такого оператора в том, что входной сигнал преобразуется в выходной вида:
![]() .
.
Полезность этой записи в том, что дифференциальные уравнения высокого порядка можно записать в краткой операторной форме.
Самыми сложными операторами, используемыми в ТАУ, являются операторы, представляющие собой отношение операторов-полиномов:
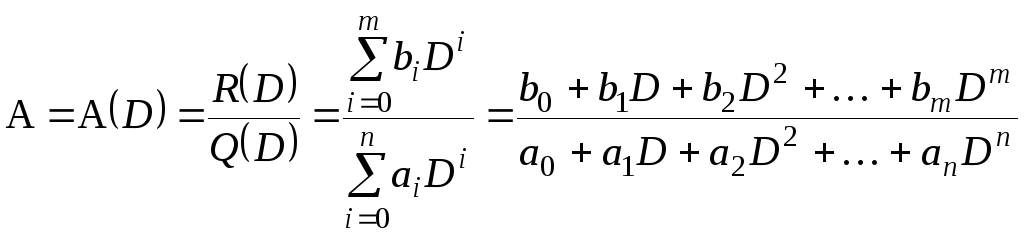 ,
,
причем
![]() – это ограничение накладывается
условиями физической реализуемости.
– это ограничение накладывается
условиями физической реализуемости.
Смысл любой операторной записи вида
![]() ,
,
заключается в том, что ей соответствует дифференциальное уравнение, связывающее вход x(t) с выходом y(t) (рис.2.3а):
![]() .
.
При
этом оператор
![]() при входной переменной
при входной переменной![]() называютоператором
воздействия,
а оператор
называютоператором
воздействия,
а оператор
![]() при выходной переменнойy
– собственным
оператором.
при выходной переменнойy
– собственным
оператором.
Математическое определение линейных САР
Выше было сказано, что непрерывные САР подразделяются на линейные и нелинейные. Для линейных систем, в отличие от нелинейных, справедлив принцип суперпозиции, математическая сущность которого заключается в следующем:
Пусть
известно, что реакцией САР (рис.2.5) на
воздействие g1(t)
является сигнал x1(t)=Ag1(t),
реакцией САР на воздействие g2(t)
– сигнал x2(t)=Ag2(t),
…,  реакцией
на воздействиеgn(t)
– сигнал xn(t)=Agn(t),
где A – оператор преобразования входной
функции в выходную. В роли воздействий
gi(t)
могут выступать как управляющие, так и
возмущающие воздействия.
реакцией
на воздействиеgn(t)
– сигнал xn(t)=Agn(t),
где A – оператор преобразования входной
функции в выходную. В роли воздействий
gi(t)
могут выступать как управляющие, так и
возмущающие воздействия.
САР является линейной, если ее реакция на линейную комбинацию функций (сигналов) gi(t), i=1,2,…,n
![]() ,
,
где ki – произвольные действительные числа, является также линейной комбинацией сигналов xi(t), i=1,2,…,n:
![]() .
.
Проще говоря, реакция линейной системы на сумму сигналов равна сумме реакций на каждый сигнал в отдельности.
Если все элементы САР (АР, ПУ, ОУ) являются линейными, то и САР в целом будет линейной. Наличие же в САР хотя бы одного нелинейного элемента делает систему нелинейной.
Линейные САР подразделяются на стационарные и нестационарные. Нестационарными являются САР, оператор A которых сам является функцией времени. Отметим, что это не противоречит принципу суперпозиции, поскольку САР остается линейной.
Большую часть реальных САР можно считать линейными, разумеется, с наложением при этом некоторых ограничений. Для получения соответствующей линейной модели используется линеаризация всех или некоторых уравнений исходной САР.
Линеаризация динамических САР
Линеаризацией нелинейных дифференциальных уравнений (ДУ) реальной САР является процесс их преобразования в линейные уравнения, суть которого заключается в следующем:
В САР должен поддерживаться некоторый заданный режим работы, в котором входные и выходные величины изменяются по определенному закону. Но из-за наличия возмущающих факторов реальные значения переменных состояния отличаются от заданных значений, причем в нормально работающей системе эти различия достаточно малы. Это позволяет разложить нелинейные функции, входящие в уравнения, в ряд Тейлора в окрестности точки, соответствующей заданному (нормальному) режиму работы САР.
Пусть процессы в реальной САР (как в установившихся, так и в переходных режимах) описывается нелинейным уравнением динамики:
![]() .
.
В качестве переменных x, y и z могут выступать воздействия на САР, а также их производные.
В установившемся режиме уравнение принимает вид:
![]() , (*)
, (*)
где
![]() ,
,![]() ,
,![]() – значения воздействий в установившемся
режиме, и называется при этомуравнением
статики.
– значения воздействий в установившемся
режиме, и называется при этомуравнением
статики.
Переменные,
входящие в исходное уравнение, для
реального режима представляются в виде
сумм их установившихся значений
![]() ,
,![]() ,
,![]() и малых приращений
и малых приращений![]() ,
,![]() и
и![]() :
:
![]() ,
,![]() ,
,![]() .
.
Подставляем эти выражения в исходную функцию, которую после разложения в ряд Тейлора, пренебрегая составляющими высших порядков малости (меньших, чем порядок приращений), можно представить в виде:
![]()
![]() .
.
Приравнивая последнее уравнение к нулю, и вычитая это уравнение из уравнения статики (*), получаем линеаризованное уравнение САР в приращениях:
![]() .
.
После указанных преобразований САР считается линейной.
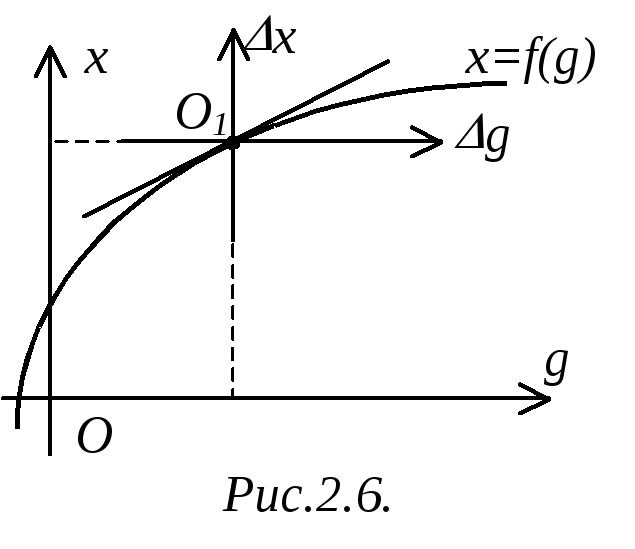 Геометрический
смысл линеаризации нелинейной зависимости
Геометрический
смысл линеаризации нелинейной зависимости
![]() между двумя переменными (рис.2.6) означает
замену исходной кривой касательной в
точкеО1,
соответствующей заданному режиму
работы, и параллельный перенос начала
координат в эту точку.
между двумя переменными (рис.2.6) означает
замену исходной кривой касательной в
точкеО1,
соответствующей заданному режиму
работы, и параллельный перенос начала
координат в эту точку.
После линеаризации символы D приращений переменных обычно опускают.
Дифференциальные уравнения линейных сар
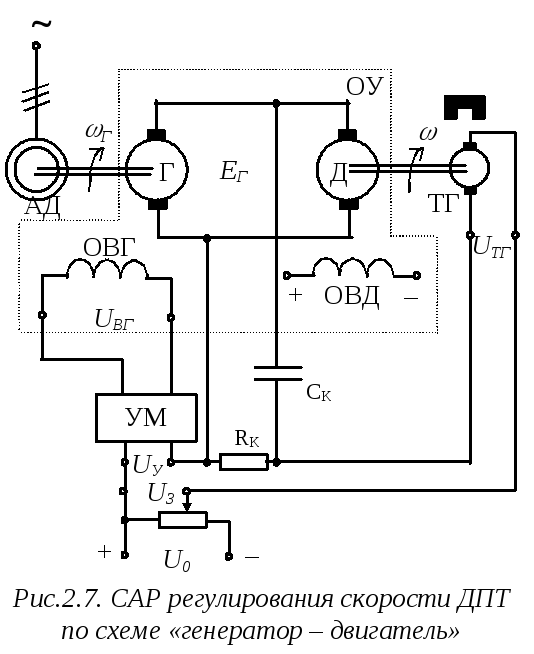
Рассмотрим САР частоты вращения двигателя постоянного тока независимого возбуждения, который питается от генератора независимого возбуждения (рис.2.7) (система «генератор – двигатель»).
Данная система, хотя еще и встречается на практике, в настоящее время является морально устаревшей. Выбор ее в данном вопросе удобен в том плане, что на ее примере можно наиболее наглядно получить типовые дифференциальные уравнения, используемые при анализе систем электропривода.
Объект управления САР содержит генератор (Г), вал которого вращается с помощью приводного АД, с обмоткой возбуждения ОВГ, и двигатель (Д) с обмоткой возбуждения ОВД. Величина ЭДС генератора EГ регулируется за счет изменения напряженияUВГна ОВГ, которое, в свою очередь формируется с помощью усилителя мощности (УМ), выполняющего роль преобразующего устройства. В качестве датчика регулируемой переменной (скорости двигателя) выступает тахогенератор постоянного тока (ТГ). Сигнал заданияUЗформируется с помощью потенциометра, и, согласно электрической цепи, выполняющей функцию узла сравнения, оказывается равным сумме напряженияUТГс выхода ТГ, напряженияUKкорректирующей цепи (RK– CK) и напряженияUУна входе УМ. Корректирующая цепь необходима для придания САР требуемых динамических свойств.
Для математического описания САР выделяют ее отдельные элементы, которые обладают однонаправленными свойствами: выходной сигнал формируется в зависимости от входного, и не влияет на него. Согласно с таким принципом однонаправленности, в САР рис.2.7 можно выделить следующие элементы:
 1.
Генератор
(Г). В качестве входа рассматриваем
напряжение возбуждения UВГ,
в качестве выхода – ЭДС генератора ЕГ.
Условно записываем:
1.
Генератор
(Г). В качестве входа рассматриваем
напряжение возбуждения UВГ,
в качестве выхода – ЭДС генератора ЕГ.
Условно записываем:
UВГ ® ЕГ (вход ® выход)
Обратное направление выбрать нельзя, поскольку ЕГ не влияет на UВГ, а лишь на частоту вращения wГ. Кроме того, это противоречит функциональному назначению генератора.
2. Двигатель (Д):
ЕГ ® w
3. Тахогенератор (ТГ):
w ® UТГ
4. Усилитель мощности (УМ) считаем идеальным (внутреннее сопротивление равно нулю):
UУ ® UВГ
5. Узел сравнения (электрическая цепь) (УС):
UУ = UЗ – UТГ – UK
6. Корректирующая цепь (КЦ):
ЕГ ® UK
После такой детализации можно изобразить блок-схему рассматриваемой САР (рис.2.8).
Отметим здесь, что рассматриваемая САР является непрерывной.
Рассмотрим теперь более детально каждый блок для того, чтобы составить его математическое описание.

Генератор
Будем считать, что все полюса генератора соединены последовательно. Уравнение электрического равновесия (рис.2.9а) имеет вид:
![]() ,
,
где
![]() – число пар полюсов генератора; WВГ
– число витков на полюс.
– число пар полюсов генератора; WВГ
– число витков на полюс.
Цепь
намагничивания генератора является
нелинейной, поскольку
![]() (рис.2.9б). Для упрощения подвергнем ее
линеаризации в окрестности рабочей
точки с координатами
(рис.2.9б). Для упрощения подвергнем ее
линеаризации в окрестности рабочей
точки с координатами![]() ,
используя соображения, рассмотренные
выше. После разложения функции
,
используя соображения, рассмотренные
выше. После разложения функции![]() в ряд Тейлора и пренебрежения малыми
членами можно получить:
в ряд Тейлора и пренебрежения малыми
членами можно получить:
![]() .
.
Приравнивая
приращения и опуская символ
![]() ,
получим окончательное линеаризованное
уравнение:
,
получим окончательное линеаризованное
уравнение:
![]() ,
,
где
![]() .
.

После линеаризации уравнение электрического равновесия ОВГ можно записать в виде:
![]() .
.
ЭДС генератора при неизменной частоте вращения вала wГ пропорциональна магнитному потоку:
![]() ,
,
где
![]() – конструктивная постоянная генератора.
– конструктивная постоянная генератора.
Выразим из последнего уравнения магнитный поток
![]()
и подставим в уравнение электрического равновесия:
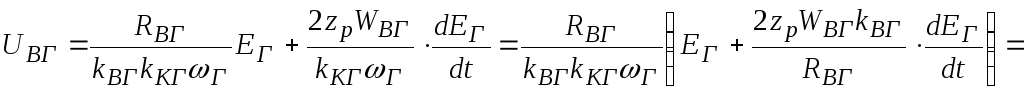
![]() ,
,
где
![]() – индуктивность возбуждения генератора.
– индуктивность возбуждения генератора.
Обозначим:
![]() –коэффициент
усиления генератора;
–коэффициент
усиления генератора;
![]() –постоянная
времени генератора, с.
–постоянная
времени генератора, с.
Теперь ДУ генератора можно записать в окончательном виде:
![]() , (1)
, (1)
где
![]() – оператор дифференцирования.
– оператор дифференцирования.
Это уравнение характеризует работу генератора как в статике, так и в динамике.
Двигатель
Двигатель постоянного тока с независимым постоянным возбуждением может быть описан следующими уравнениями:
Уравнение электрического равновесия цепи якоря:
![]() ,
,
где
![]() ,
,![]() – суммарные активное сопротивление и
индуктивность цепи обмотки якоря
двигателя, представляющие собой суммы
соответствующих параметров генератора
и двигателя,
– суммарные активное сопротивление и
индуктивность цепи обмотки якоря
двигателя, представляющие собой суммы
соответствующих параметров генератора
и двигателя,![]() – противо-ЭДС двигателя;
– противо-ЭДС двигателя;![]() ;
;![]() – конструктивная постоянная двигателя;
– конструктивная постоянная двигателя;![]() – магнитный поток двигателя.
– магнитный поток двигателя.
Уравнение электромагнитного момента:
![]() .
.
Уравнение механической части (уравнение движения):
![]() .
.
Будем
считать пока, что нагрузка на валу
двигателя отсутствует (![]() ).
Уравнение момента подставим в уравнение
движения, после чего выразим ток:
).
Уравнение момента подставим в уравнение
движения, после чего выразим ток:
 .
.
Выражение для тока подставим в уравнение электрического равновесия:
![]() .
.
Разделив
это уравнение на
![]() ,
получим ДУ двигателя в окончательном
виде:
,
получим ДУ двигателя в окончательном
виде:
![]() , (2)
, (2)
где
![]() – электромагнитная постоянная времени
цепи якоря, с;
– электромагнитная постоянная времени
цепи якоря, с;
![]() –электромеханическая
постоянная времени привода, с.
–электромеханическая
постоянная времени привода, с.
Тахогенератор
Если пренебречь оборотными пульсациями и внутренним сопротивлением тахогенератора, то напряжение на его выходе (равное наводимой ЭДС):
![]() , (3)
, (3)
где
![]() – коэффициент передачи тахогенератора,
В*с.
– коэффициент передачи тахогенератора,
В*с.
Усилитель мощности
Пренебрегая внутренним сопротивлением усилителя мощности, для напряжения возбуждения генератора запишем уравнение:
![]() , (4)
, (4)
где
![]() – коэффициент передачи усилителя
мощности.
– коэффициент передачи усилителя
мощности.
Узел сравнения
Составленное ранее уравнение оставляем без изменения:
![]() . (5)
. (5)
Цепь корректирования
 ДУ
для цепи корректирования (рис.2.10) имеет
вид:
ДУ
для цепи корректирования (рис.2.10) имеет
вид:
![]()
или
![]() , (6)
, (6)
где
![]() – постоянная времени цепи, с.
– постоянная времени цепи, с.
Очевидно,
цепь корректирования работает только
в переходных режимах. В установившихся
режимах, когда
![]() ,
правая часть (6) равна нулю.
,
правая часть (6) равна нулю.
