9. Частотные характеристики САУ: комплексный коэффициент

усиления, АЧХ, ФЧХ, ВЧХ,МЧХ,АФХ,ЛАЧХ,ЛФЧХ.

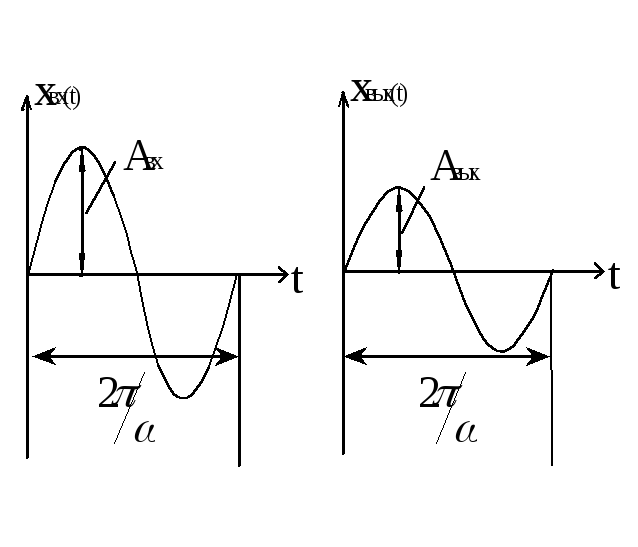
Частотные характеристики САУ.

 

Формула Эйлера.

Запишем входной и выходной сигнал в комплексной форме (используя формулу Эйлера).

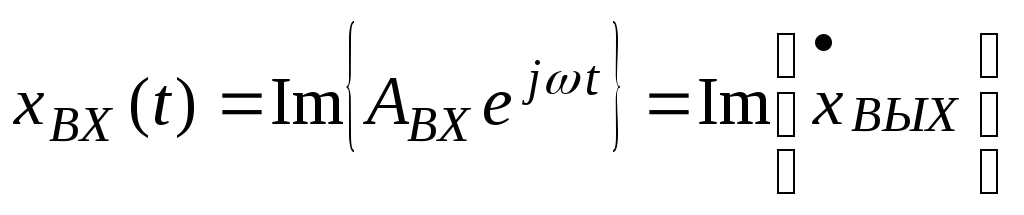
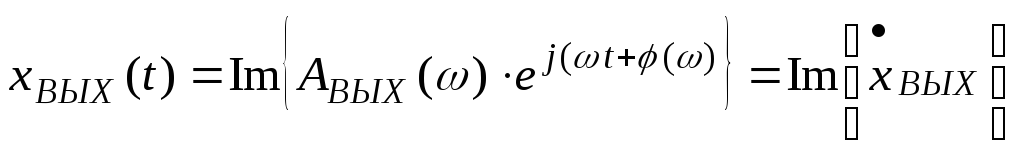
Вводится понятие комплексного коэффициента усиления (ККУ)

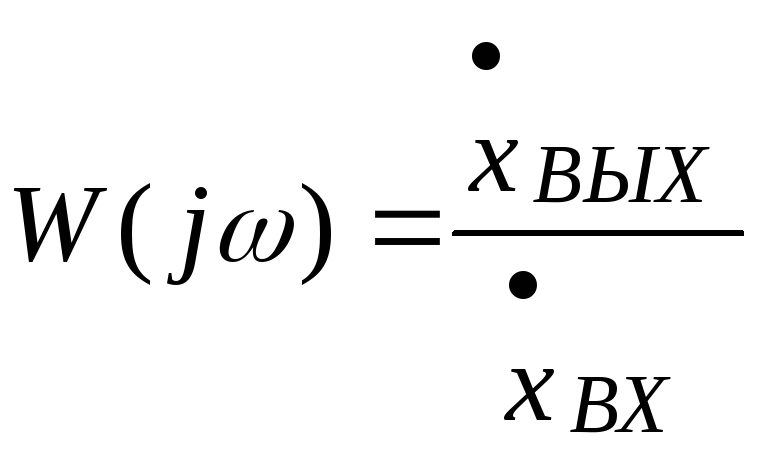
Определение:

ККУ – это отношение выходного сигнала к входному в установившемся режиме, записанных в комплексной форме.

 

j

ABX(длина)

+

АВЫХ

 

 

Вектора вращаются против часовой стрелки со скоростью , а сигнал это проекция векторов на мнимую часть.

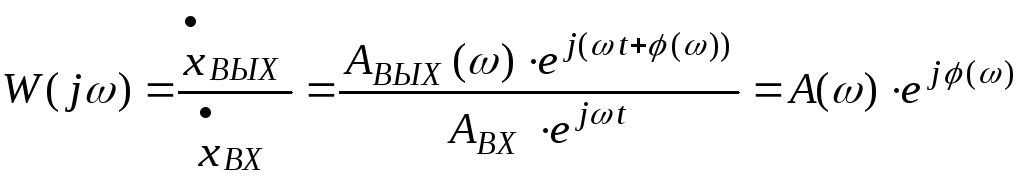
где

А() – это АЧХ амплитудно-частотная характеристика, это отношение амплитуды выходного сигнала к амплитуде входного сигнала на определенной частоте (при подаче на вход гармонического сигнала частоты ).

- фазо-частотная характеристика – это разность фаз, между выходным и входным сигналом при подаче на вход сигнала определенной частоты.

Если разложить по формуле Эйлера то:

где :

Геометрическая интерпретация ККУ

 

 

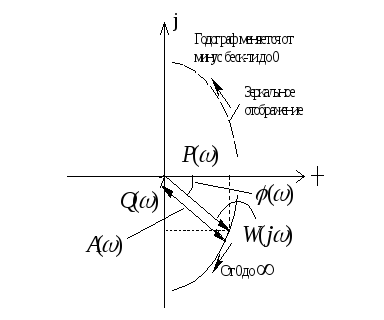
Опрделение:Геометрическое место точек конца вектора называется годографом (Найквиста), или амплитудно-фазовой характеристикой АФХ.

Частота меняется:

Используемые в ТАУ характеристики.

1). АЧХ – амплитудно – частотная характеристика. Строится в обычном масштабе по частоте от 0 до Строится по выражению .

2). ФЧХ – фазо-частотная характеристика. Строится по выражению на диапазоне частот от 0 до .

3). ВЧХ – Вещественная частотная характеристика. Строится по выражению на диапазоне частот от 0 до .

4). МЧХ – мнимая частотная характеристика. Строится по выражению на диапазоне частот от 0 до

5). АФХ – амплитудно-фазовая характеристика. Строится по выражению на комплексной плоскости при изменении частот либо от 0 до либо от.

6). ЛАЧХ – логарифмическая амплитудно-частотная характристика

Строится в логарифмическом масштабе при изменении частоты от 0 до .

 

 

 

Децибелла – логарифмическая единица измерения отношения 2-х величин.

Декада – диапазон частот на котором частота изменяется в 10 раз.

6). Ассимптотическая ЛАЧХ - - это характеристика полученная из апрксимацией её отрезками прямых с наклонами:

7). ЛФЧХ – логарифмическая фазо-частотная характеристика. Строится в полулогарифмическом масштабе в диапазоне частот от 0 до .

Обычный масштаб

(-1)

(0)

(1)

(2)

 

10

0.1

 

 

10. Частотные характеристики интегрирующего и инерционного

звеньев.

Интегрирующее звено:

Передаточная функция:

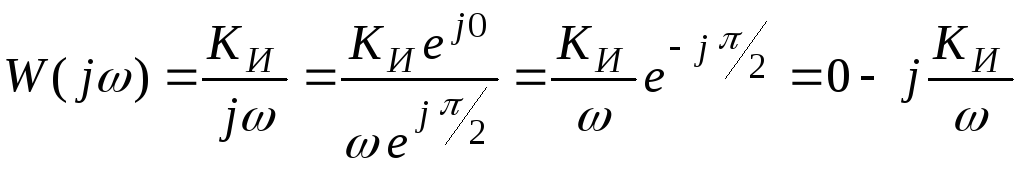
где: 0 = P()

= Q()

= A()

j

jK

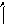
K

+

+

Построим характеристики.

 

1). АЧХ

 

 

 

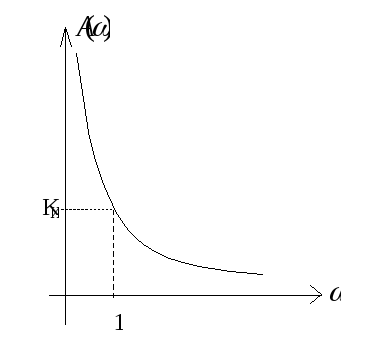
Если на С подать сигнал нулевой частоты напряжение U_C растет до бесконечности {речь идет видимо о схеме замещения интегрирующего звена}.

Если

2).ФЧХ – фазо-частотная характеристика.

 

 

 

 

 

 

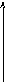
3). АФХ – (годограф).

j

0

 

+

0

 

 

4).Действительная частотная характеристика равна нулю.

Мнимая частотная характеристика МЧХ.

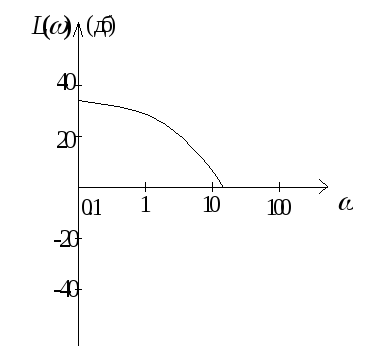
5). Логарифмическая АЧХ (ЛАЧХ)

 

40

 

20lgK

20

100

1

-20

 

Наклон 20 дб/дек, коэффициент усиления К==10

6). ЛФЧХ.

 

 

0.1

10

100

Инерционное звено.

Передаточная функция:

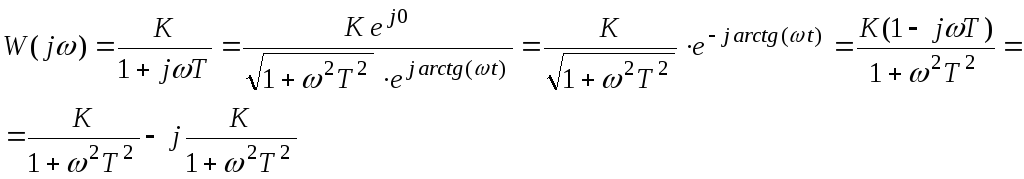
где: P() =

Q() =

А() =

 

Перейдем к построению характеристик.

 

 

1). АЧХ (А()).

 

 

 

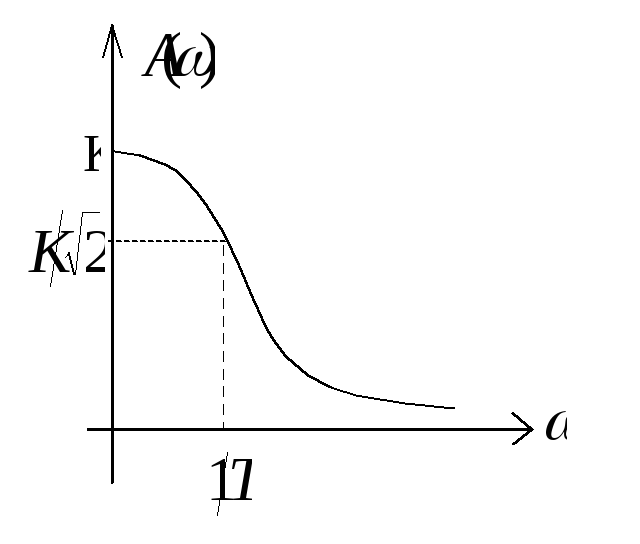
2). ФЧХ ()

 

 

 

 

 

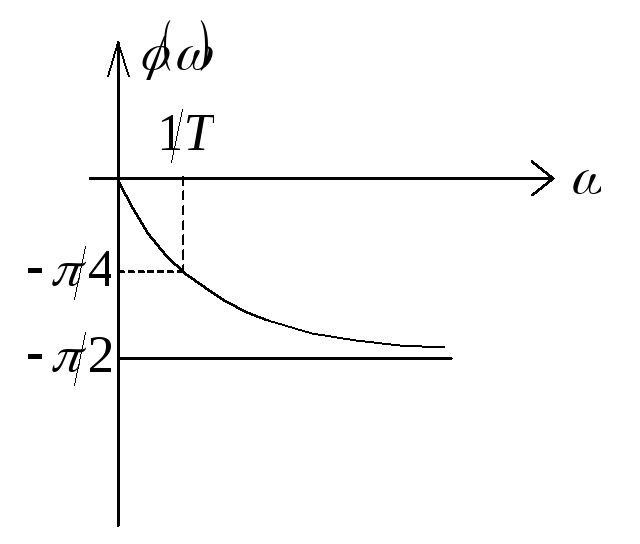
3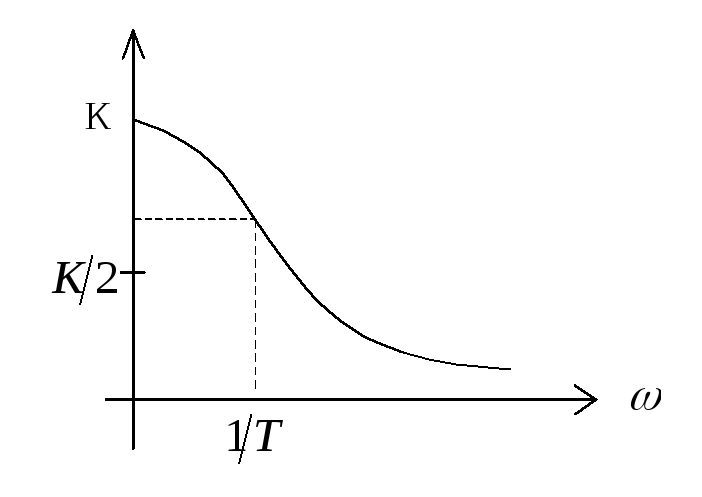 ). ВЧХ (Р())

 

4). МЧХ (Q())

5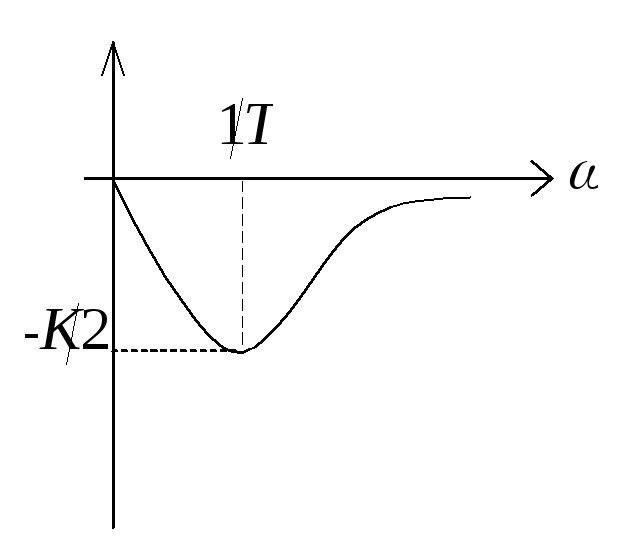 ). АФХ (W())

Г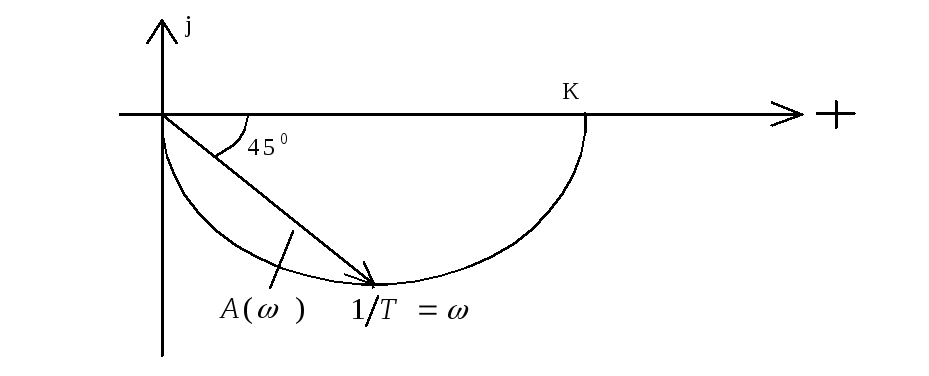 одограф входит в 0 под углом так как при

 

 

 

 

11. Частотные характеристики колебательного и звена запазды-

вания.

Колебательное звено.

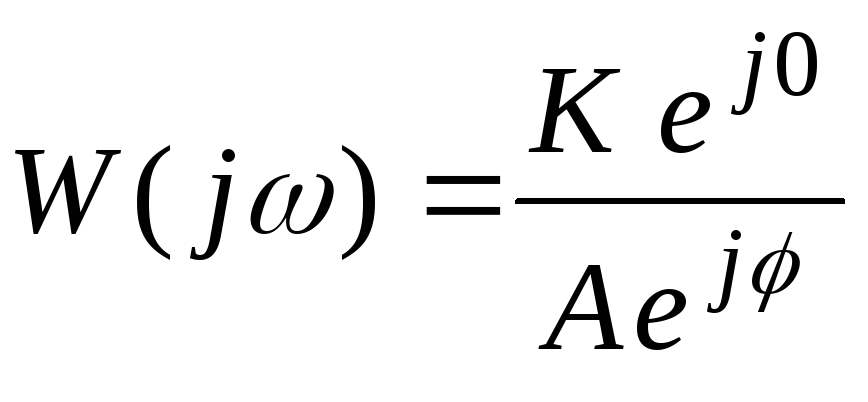
j

 

 

+

 

 

 

 

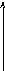
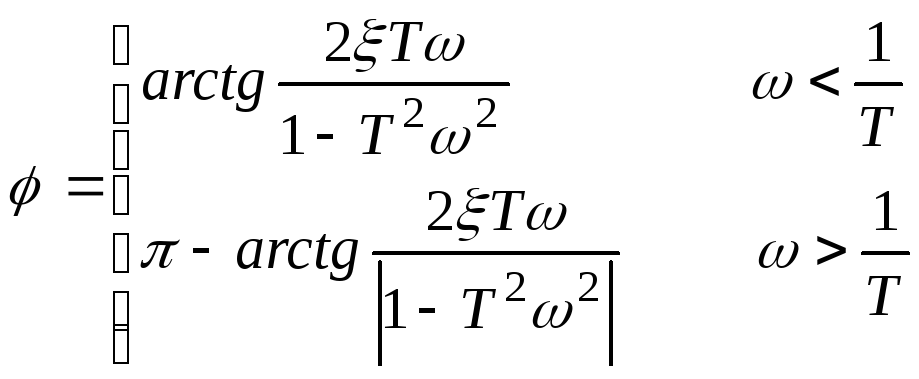
АЧХ – амплитудно-частотная характеристика

 

 

 

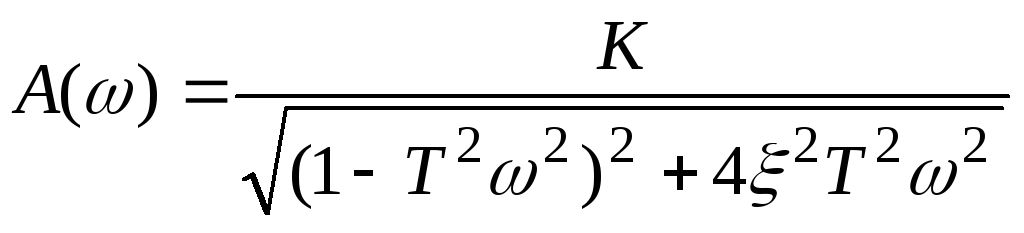
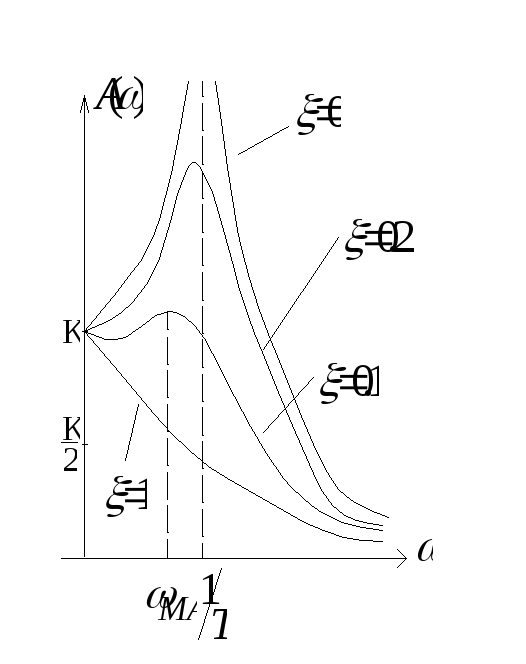
- резонансная частота.

Рассмотрим разные значения

 

ФЧХ.

 

 

 

 

 

 

 

 

 

 

 

 

 

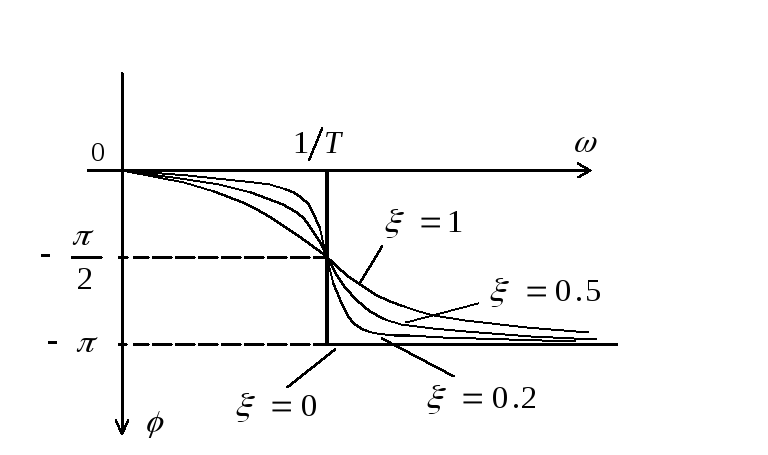
П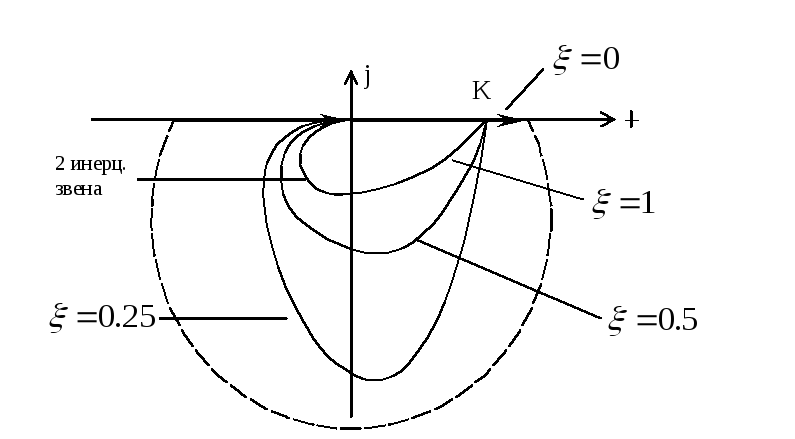ерейдем к построению годографа АФХ ()

 

 

 

Годограф приходит в ноль под углом (). При годограф идет от К по оси, затем при разрыв и входит в 0 по оси (генератор незатухающих колебаний).

 

 

 

 

 

 

 

ЛАЧХ

 

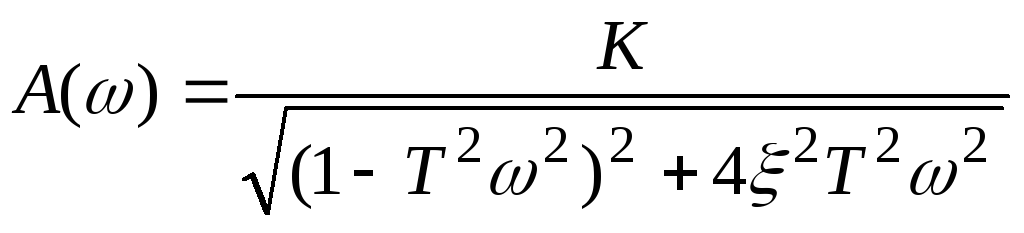
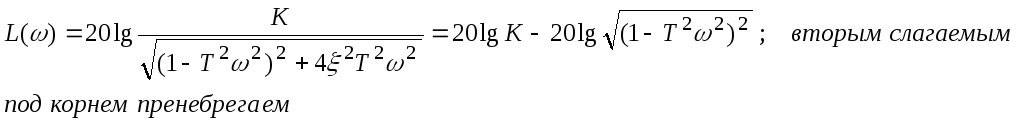
Строится асимптотическая ЛАЧХ.

1)

2)

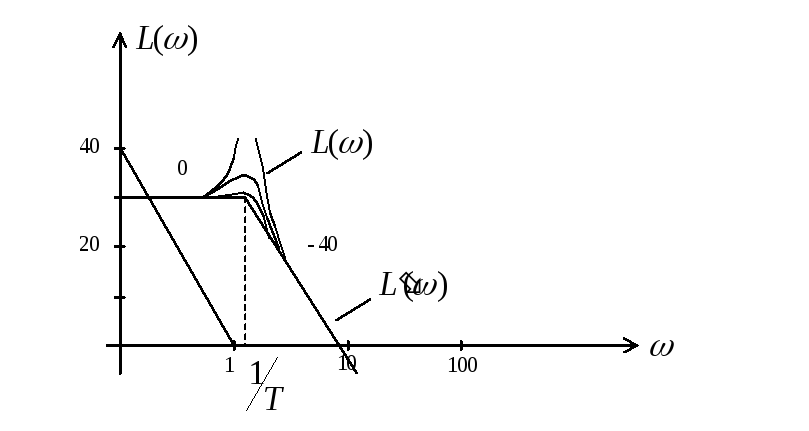
ЛФЧХ

 

 

Звено запаздывания

 

 

 

 

АЧХ

 

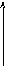
К

 

 

 

 

ФЧХ

 

 

 

 

 

 

 

 

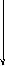
- годограф

 

j

 

+

K

- K

 

 

 

 

12. Частотные характеристики идеального и реального дифферен-

цирующих звеньев.

 

Пропуск.

 

13. Построение логарифмических частотных характеристик по пере-

даточной функции разомкнутой системы.

 

где:

 

Построение ЛАЧХ:

- асимптотическая ЛАЧХ.

- частота сопряжения.

1).

2).