лекции / вордовские / Лекции по ТАУ(часть6)

Нелинейные законы регулирования.

1. Идеальное (двухпозиционное) реле.

 

ХАР

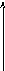
+В

 

Х

-В

 

 

2. Трехпозиционное реле (реле с зоной нечувствительности).

 

ХАР

+В

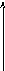
-а

Х

а

-В

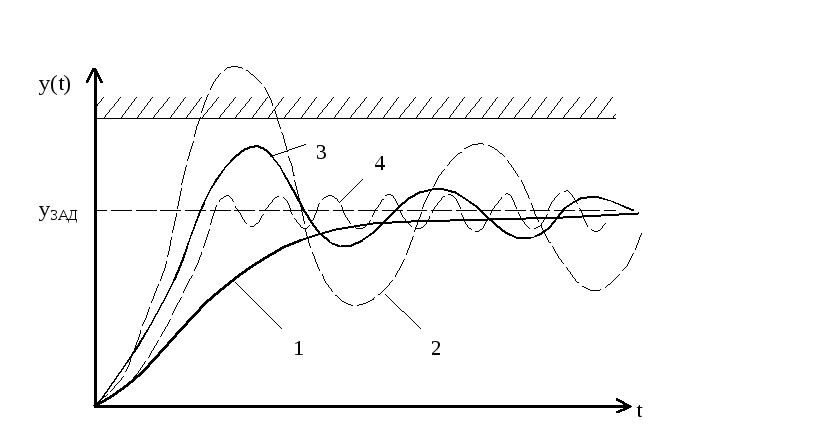
Нелинейные законы регулирокания могут обеспечить в системе качественно новые процессы:

Пример:

Где: 1 – линейный регулятор 2.

2 – у без регулирования.

3. – линейный регулятор 1.

4. – нелинейный регулятор.

 

у – выходная величина процесса, которую надо поддерживать на уровне у_ЗАД (например химический процесс).

 

5. Статическая система автоматического управления на примере САР скорости вращения двигателя постоянного тока с независимым возбуждением.Статические характеристики САР.

 

Система автоматического регулирования (САР) скорости вращения двигателя постоянного тока с независимым возбуждением.

 

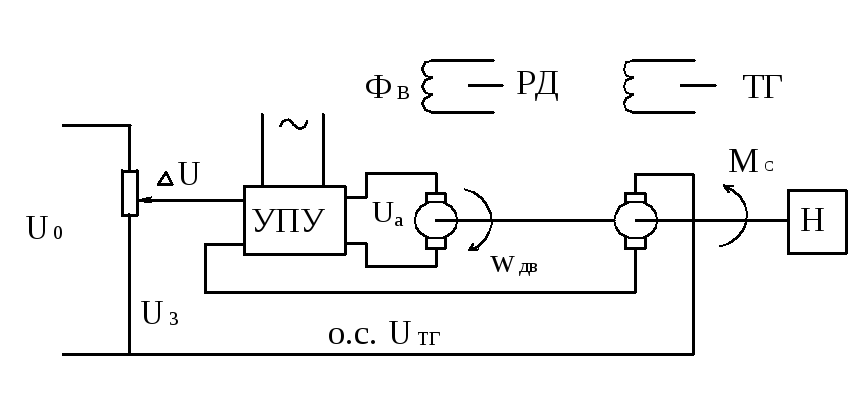
U₀ – напряжение, поступающее на вход потенциометра.

U_З – напряжение, задающее скорость вращения двигателя.

РД – реверсивный двигатель.

ТГ – тахогенератор (устройство для измерения скорости вращения двигателя).

УПУ – усилительно-преобразовательное устройство.

Н – нагрузка или производственный механизм, скорость которого надо поддерживать постоянной.

U_а – напряжение на якорной обмотке двигателя.

- скорость вращения двигателя.

U_ТГ – напряжение на выходе ТГ.

М_С – момент сопротивления на валу двигателя.

Ф_В – ЭМ поток возбуждения двигателя.

РД – объект управления.

УПУ+ТГ=АР – автоматический регулятор.

- задающее воздействие.

- регулируемая величина.

М_С – возникающее воздействие.

- ошибка

U_ТГ – подается через отрицательую обратную связь.

Цель системы: Стабилизация скорости вращения двигателя.

Рассмотрим момент времени t₀.

Все сигналы постоянны.:

Теперь рассмотрим момент времени t₁.

Сигналы изменяются:

М_С-возрастает скачком (изменяется нагрузка). Следовательно: - падает, U_ТГ – падает, - возрастает, U_а – возрастает, следовательно возрастет , т.е осуществляется регулировка.

 

1. «И» закон регулирования.

Для момента времени t₂:

Допустим, что - возрастает.

Единственная точка стабилизации:

Для «И»:

Определение: Астатической называется система, у которой выходнаявеличина не зависит от возмущения (статическая ошибка равна нулю).

 

 

 

МС

 

 

2. Пропорциональный закон регулирования.

 

Предположим, что ошибка:

, наше предположение не верно, т.е

 

 

 

 

 

 

 

МС

 

Определение: Статической называется система автоматического регулирования (САР), у которой выходная величина уменьшается при увеличении возмущения. Статическая ошибка в такой системе на равна нулю.

 

Статические характеристики статической САР.

Определение: Статические характеристики - характеристики, полученные в положении равновесия.

Статические характеристики двигателя постоянного тока.

 

 

 

U_a – напряжение на якорной обмотке двигателя.

I_a – ток в якорной цепи.

Ф_В – ЭМ. поток возбуждения.

- скорость вращения двигателя.

М_С – момент сопротивления на валу.

При взаимодействии тока i_a и потока Ф_В на валу возникает момент вращения двигателя М_ДВ.

Ф_В = const, если реакцией якоря можно пренебречь, то

1) Если М_С = 0, то

Насыщение системы

 

 

Ua

 

2) U_a – const.

Ua2

Если Ua = 0

Ua1

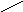
MC

Ua=0

 

 

 

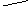
Статическая характеристика двигателя постоянного тока:

{по поводу степени «с» в лекциях написано, что она статическая и формируется системой}

К

 

К – коэффициент усиления разомкнутой системы.

 

 

(**)

 

 

 

 

Уравнения статики статической системы.

Найдем статическую ошибку.

 

 

 

 

Статическая ошибка статической системы

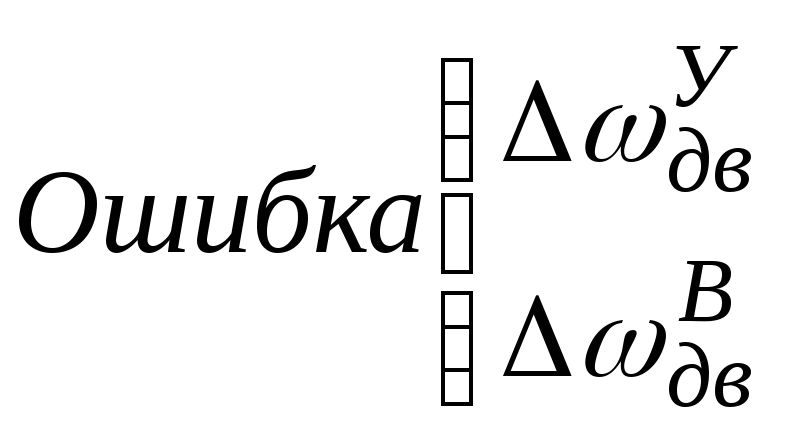
Индексы: у - по управляющему воздействию, В – по возмущающему воздействию.

Что дает отрицательная обратная связь (замыкание системы)?

Момент изменяется от 0 до М_С - разомкнутая система, - изменение скорости двигателя.

Для замкнутых систем скорость изменилась:

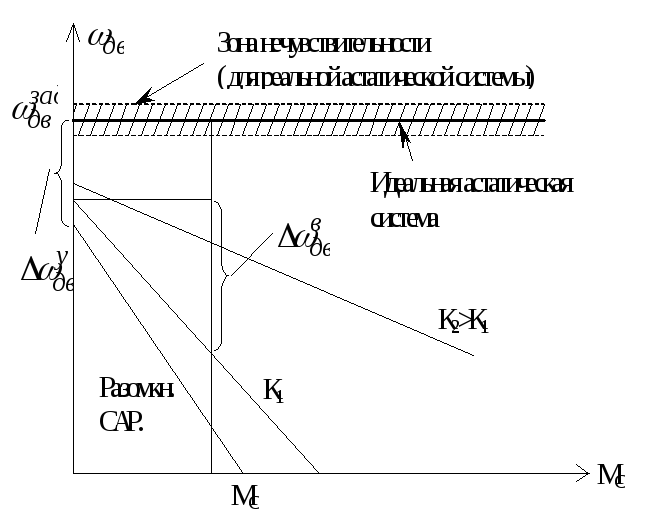
Вывод: При замыкании системы статическая ошибка по возмущению уменьшается в (1+К) раз.

Построим статические характеристики по выражению (**).

 

 

6. Линеаризация. Вывод уравнений генератора постоянного тока с рабочей точкой в нелинейной зоне.

Л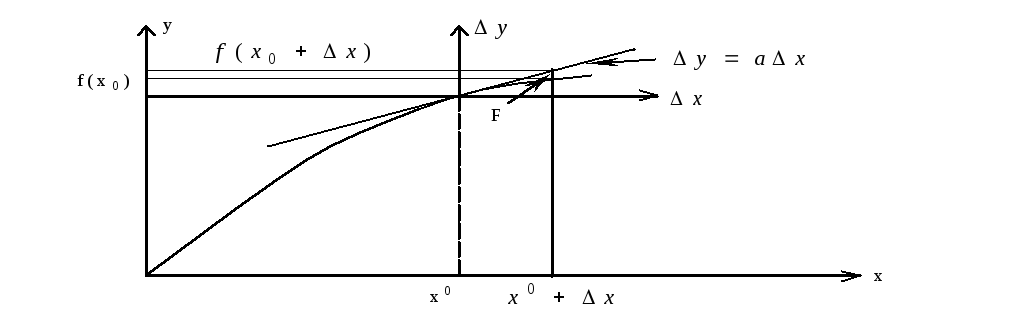 инеаризация – замена нелинейных уравнений на линейные, проводится в пределах заданной точности и используется для исследования линейных систем.

 

Рассмотрим точку х⁰ вблизи которой мы хотим получить наше уравнение.

Зададим приращение

Разложение в ряд Тейлора.

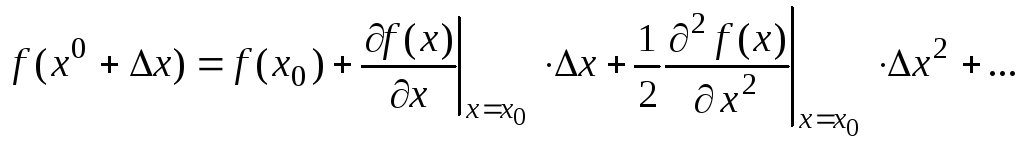
F

 

Отбрасываем члены F.

Получаем линеаризованное ур-е.

Линеаризованное ур-е в приращениях:

Переносим начало координат из точки 0 в точку 0’.

F – ошибка линеаризации.

 

Получение линеаризованныхуравнений

генератора постоянного тока на холостом ходу.

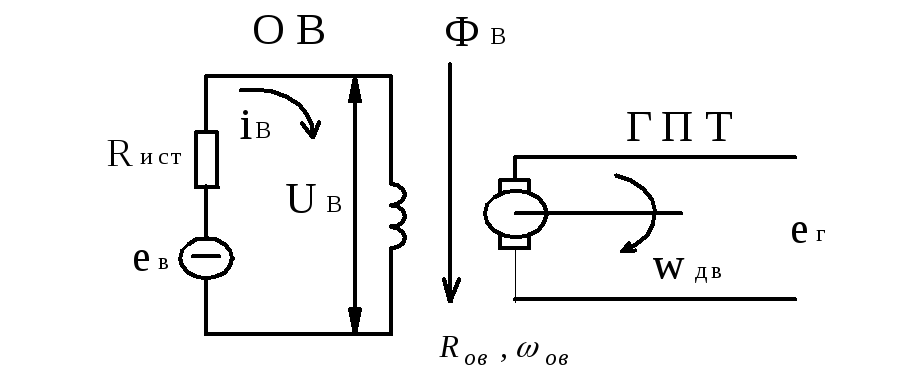
ОВ – обмотка возбуждения.

ГПТ – генератор постоянного тока.

R_ИСТ – активное сопротивление источника питания.

е_В – ЭДС источника питания (возбуждения).

i_B, U_B – ток и напряжение на обмотке возбуждения.

Ф_В – ЭМ поток, создаваемый обмоткой возбуждения.

- скорость, с которой посторонний двигатель вращает якорь генератора постоянного тока.

е_г – ЭДС генератора.

R_ОВ – активное сопротивление обмотки возбуждения

- числовитков обмотки возбуждения.

Уравнение обмотки возбуждения.

ОВ: 1)

2

ЭДС самоиндукции

)

 

 

 

3) ГПТ – цепь генератора

С_Г – некоторая константа (можно, конечно, вспомнить из машин, но лень).

Уравнения 1-3 это описание ГПТ в виде нелинейных диф. уравнений.

1. 1)     Если шириной петли гистерезиса пренебречь нельзя, то линеаризация невозможна, и для описания требуется привлечение аппарата анализа нелинейных систем.

2. 2)     Если ширина петли гистерезиса мала, то 2-ух значная характеристика заменяется на 1-но значную (средняя линия петли гистерезиса).

Рассмотрим 2 участка.

 

 

Получение линеаризованных уравнений ГПТ для рабочей точки в нелинейной зоне

 

 

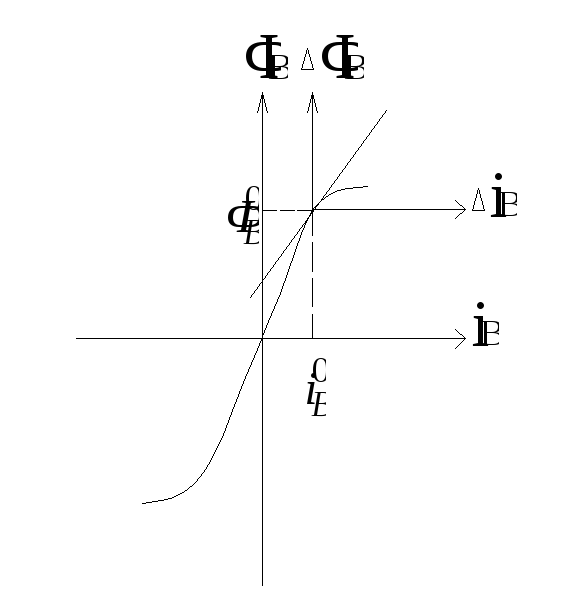
Получим систему линеаризованных уравнений.

Получим ур-е стационарной точки (рабочей точки)

В стационарной точке все вх. и вых. постоянны, все производные равны нулю.

2-а уравнения стационарной точки:

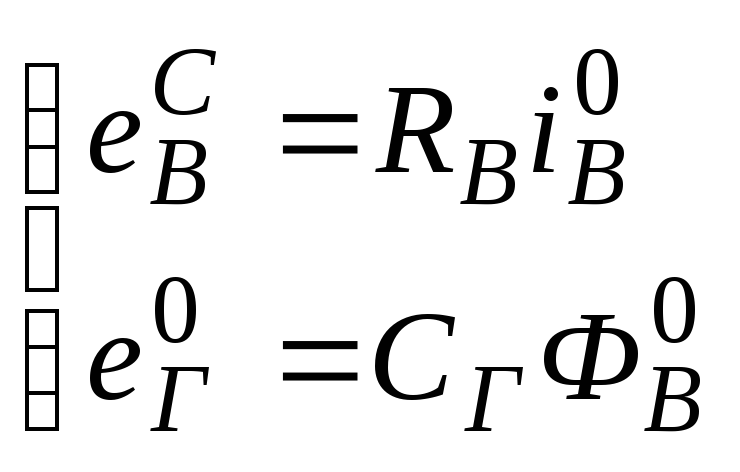
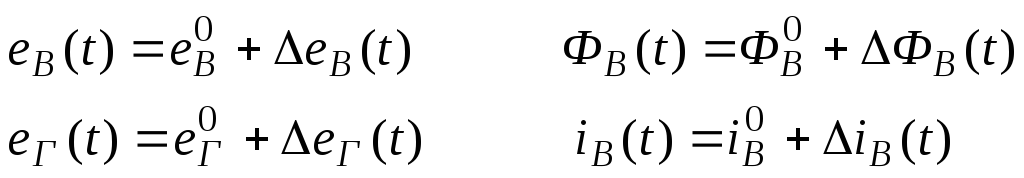
где - рабочая точка, а - приращение от этой рабочей точки.

 

1')

2’)

3’)

Уравнения 1’-3’ это линеаризованные уравнения в приращениях, описывающие работу генератора постоянного тока вблизи рабочей точки.

 

7. Линеаризация. Вывод уравнений генератора постоянного

тока с рабочей точкой в линейной зоне.

2”)

индуктивность 1-го витка обмотки возбуждения.

1”)

LB

 

-число витков обмотки возбуждения.

L_B – индуктивность обмотки возбуждения.

3”)

Уравнения 1”-3”это линейные уравнения, описывающие работу ГПТ в линейной зоне.

 

8. Свойства преобразования Лапласа. Передаточные функции.

Передаточные функции используют преобразования Лапласа.

Преобразование Лапласа его свойства.

Оригинал изображения по Лапласу

р – комплексная величина, оператор Лапласа.

Формула преобразования Лапласа:

Преобразование Лапласа заменяет решение дифференциальных уравнений во временной области, решением алгебраических уравнений в плоскости р,что облегчает задачу.

Свойства преобразования Лапласа

1. Линейность

Таким образом преобразование Лапласа от суммы равно сумме преобразований Лапласа.

2. Изображение производных.

3. Преобразование Лапласа от интеграла (Изображение интеграла).

4. Изображение Лапласа от функции с запаздывающим аргументом.

Функция с запаздывающим аргументом:

 

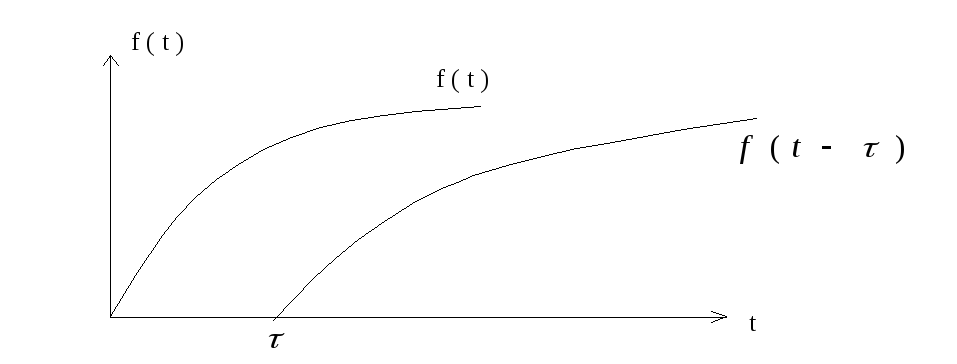
- оператор запаздывания.

5.Теорема о конечном значении.

Если предел существует, это означает, что поведение функции в бесконечности, определяется поведением её изображения в нуле.

Понятие передаточной функции.

САУ

xBX(t)

xВЫХ(t)

W(p)

 

Передаточной функцией (W(p)) называется отношение изображения выходного сигнала при нулевых начальных условиях (ННУ).

ННУ – означают, что входной и выходной сигнал вместе с их (n-1) производными равен нулю.

1.Пример получения передаточной функции.

Передаточная функция ГПТ.

Воздействуем оператором Лапласа на правую и левую дифференциального уравнения.

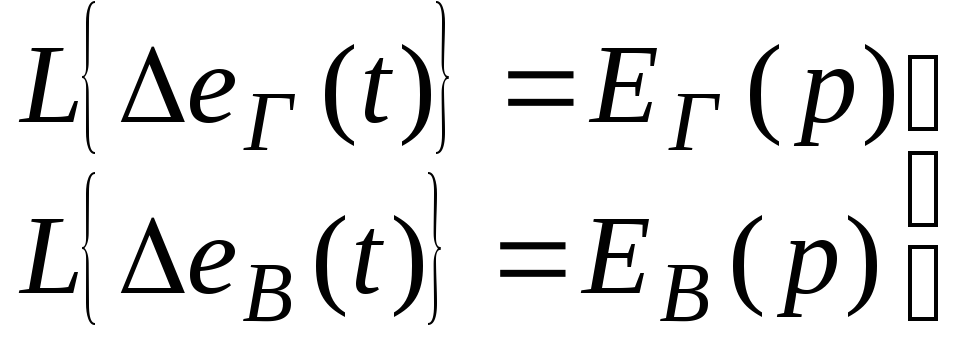Введем обозначения.

Передаточная функция: