
- •8.2. Построение экономико-математических моделей задач линейного программирования
- •8.3. Графическое решение задачи линейного программирования
- •8.4. Анализ моделей на чувствительность
- •8.5. Симплекс – метод. Общая идея симплекс – метода
- •8.6. Методы нахождения опорного решения задачи линейного программирования
- •8.7. Экономическая интерпретация решения задачи линейного программирования
- •8.8. Двойственные задачи линейного программирования. Взаимодвойственные задачи
- •8.9. Экономико-математический анализ полученных оптимальных решений
- •Итоговая таблица
- •Задачи Построить математическую модель задачи линейного программирования (8.1 — 8.30).
- •Решите задачи линейного программирования (8.31 — 8.60) графическим методом, проведите анализ на чувствительность.
- •Задачи линейного программирования (8.61 – 8.90) решите симплекс-методом и проведите анализ моделей на чувствительность, сформулируйте двойственную задачу к исходной и решите её.
- •9. Транспортные задачи линейного программирования
- •9.1. Постановка задачи
- •Исходные данные
- •9.2. Алгоритм метода потенциалов
- •Исходные данные
- •Начальный план перевозок
- •Оптимальный план перевозок
- •9.3. Усложненные задачи транспортного типа
- •Исходные данные
- •Оптимальное решение
- •Исходные данные
- •Исходные данные
- •Оптимальное решение
- •10. Математическое моделирование управления рынком
- •10.1. Общий подход к разработке аналитической математической модели управления рынком
- •10.2. Содержательная характеристика особенностей модели сэо
- •10. 3. Методы обоснования модели сэо
- •10.4. Основные компоненты модели
- •1.Оценивание требует:
- •2.Оценивание предполагает:
- •3.Оценивание позволяет:
- •11. Основы математического моделирования управления рынком (На примере управления рынком труда)
- •11.1 Механизмы регулирования занятости: понятие, теории и уровни его регулирования
- •11.2. О диалектических связях в развитии рынка труда и занятости сэо
- •11.3 Общий подход к формированию системы рынка труда и занятости населения
- •12. Алгоритмическое обеспечения управления системой рынка труда и занятости населения
- •12.1 Обоснование методологических основ деятельности администрации
- •12.2 Алгоритмическое обеспечение управления системой рынка труда и занятости
- •1.Оценивание требует:
- •2.Оценивание предполагает:
- •3.Оценивание позволяет:
- •12.3 Разработка алгоритма реализации модели поставки ресурсов на рынок труда в условиях воздействия разнородных факторов
- •12.4 Разработка алгоритма реализации комплексной модели информационно-управляющей системы рынка труда и занятости населения
- •Приложение 1
- •Приложение 2
- •Литература
- •Содержание
- •В.Г. Бурлов математические методы моделирования в экономике
Исходные данные
|
Потребители
Поставщики |
В1 |
В2 |
Запас, тыс.т |
|||||
|
|
|
|
|
|
|
|||
|
А1 |
|
1 |
M |
1 |
1.5 |
M |
1.5 |
3 |
|
|
M |
1 |
1 |
M |
1.5 |
1.5 |
4 |
|
|
А2 |
|
2 |
M |
2 |
1 |
M |
1 |
5 |
|
|
M |
2 |
2 |
M |
1 |
1 |
2 |
|
|
А3 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1.25 |
|
Спрос, тыс. т |
|
2 |
3 |
2 |
1 |
1.5 |
5.75 |
15.25 |
Перевозки
от фиктивного поставщика не производятся,
поэтому
![]() .
Величина M
намного больше
.
Величина M
намного больше
![]() .
Применяя метод потенциалов, в итоге
получим таблицу с. оптимальным решением
(табл. 8.7).
.
Применяя метод потенциалов, в итоге
получим таблицу с. оптимальным решением
(табл. 8.7).
Анализ решения. Первый поставщик поставит на первый элеватор (В1) пшеницу III класса (x22 — 2); пшеницу IV класса (x22 = 3), а также пшеницу любого класса (III или IV) (x13 = 1;x23=1)
Второй поставщик (А2) поставит на второй элеватор (В2) пшеницу III класса (x31 = 0* пшеницу IV класса (x45 = 1,5) и частично любую пшеницу (х36 = 4; х46 = 0,5). Потребность элеватора в любой пшенице не удовлетворена на 1,25 тыс. т (x56 = 1,25). Минимальные затраты на перевозку составили: Zmin = 14 д. е.
Таблица 9.7
Оптимальное решение
|
Потребители
Поставщики |
В1 |
В2 |
Запас, тыс.т |
|||||
|
|
|
|
|
|
|
|||
|
А1 |
|
1 2 |
M |
1 1 |
1.5 |
M |
1.5 |
3 |
|
|
M |
1 3 |
1 1 |
M |
1.5 |
1.5 |
4 |
|
|
А2 |
|
2 |
M |
2 |
1 1 |
M |
1 4 |
5 |
|
|
M |
2 |
2 |
M |
1 1,5 |
1 0,5 |
2 |
|
|
А3 |
|
0 |
0 |
0 |
0 |
0 |
0 1,25 |
1.25 |
|
Спрос, тыс. т |
|
2 |
3 |
2 |
1 |
1.5 |
5.75 |
15.25 |
Пример 9.2. Модель производства с запасами.
Фирма переводит свой головной завод на производство определенного вида изделий, которые будут выпускаться в течение четырех месяцев, величины спроса в течение этих четырех месяцев составляют 100, 200, 180 и 300 изделий соответственно. В каждый месяц спрос можно удовлетворить за счет:
-
запасов изделий, произведенных в прошлом месяце, сохраняющихся для реализации в будущем;
-
производства изделий в течение текущего месяца;
-
избытка производства изделий в более поздние месяцы в счет невыполненных заказов.
Затраты на одно изделие в каждом месяце составляют 4 д. е. Изделие, произведенное для более поздней реализации, влечет за собой дополнительные издержки на хранение в 0,5 д. е. в месяц. С другой стороны, каждое изделие, выпускаемое в счет невыполненных заказов, облагается штрафом в размере 2 д. е. в месяц.
Объем производства изделий меняется от месяца к месяцу в зависимости от выпуска других изделий. В рассматриваемые четыре месяца предполагается выпуск 50, 180, 280 и 270 изделий соответственно.
Требуется составить план, имеющий минимальную стоимость производства и хранения изделий.
Решение
Задачу можно сформулировать как транспортную. Эквивалентность между элементами производственной и транспортной систем устанавливается следующим образом:
|
Транспортная система |
Производственная система |
|
1. Исходный пункт i |
1. Период производства i |
|
2. Пункт назначения j |
2. Период потребления j |
|
3. Предложение в пункте i |
3. Объем производства за период i |
|
4. Спрос в пункте j |
4. Реализация за период j |
|
5. Стоимость перевозки из i и j |
5. Стоимость производства и хранения за период i и j |
Перед нами структура транспортной модели. Для рассматриваемой задачи стоимость «перевозки» изделия из периода i в период j выражается как:

Из
определения
![]() следует, что затраты
в период i
при реализации продукции в тот же
период i
(i=j)
оцениваются только
стоимостью производства. Если в
период i
производится продукция, которая будет
потребляться позже (i<j),
то имеют место дополнительные
издержки, связанные с хранением.
Аналогично производство в /-и период
в счет невыполненных заказов i>j
влечет за собой
дополнительные расходы в виде штрафа.
Например,
следует, что затраты
в период i
при реализации продукции в тот же
период i
(i=j)
оцениваются только
стоимостью производства. Если в
период i
производится продукция, которая будет
потребляться позже (i<j),
то имеют место дополнительные
издержки, связанные с хранением.
Аналогично производство в /-и период
в счет невыполненных заказов i>j
влечет за собой
дополнительные расходы в виде штрафа.
Например,
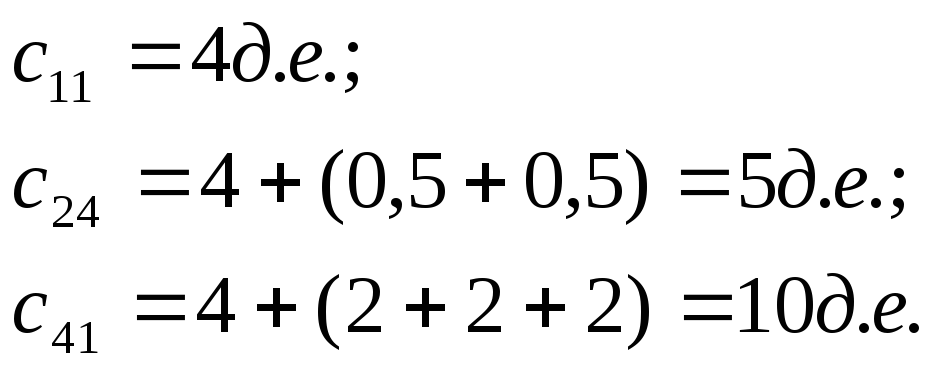
Исходная транспортная таблица выглядит следующим образом (табл. 8.8).
Задача решается обычным методом потенциалов на минимум затрат по производству и хранению продукции.
Таблица 9.8
