3. Коэффициенты полных материальных затрат в матричных моделях баланса

Прямые материальные затраты, выраженные в форме матрицы пря­мых материальных затрат, отражают затраты продукции конкретной от­расли на единицу валового выпуска продукции соответствующей отрасли.

Полные материальные затраты складываются из прямых материаль­ных затрат и косвенных затрат продукции отраслей всех порядков. Кос­венные затраты осуществляются не прямо на данный продукт, а через промежуточные продукты. Признаком порядка косвенных затрат является количество промежуточных продуктов.

Если продукт прямо не затрачивается на производство единицы этой же продукции, то полные затраты могут иметь место за счет косвенных за­трат этого же продукта через другие продукты. Полные затраты в одних случаях незначительно превышают прямые материальные затраты, в дру­гих - это превышение может быть существенным. Это зависит не только от технологии производства каждого вида продукции конкретными отрас­лями, но и от взаимосвязи между ними.

Показатели полных затрат позволяют предельно точно рассчитать по­требность в средствах производства для развития той или иной отрасли. Кроме того, показатели полных материальных затрат позволяют анализировать структуру полных затрат на производство продукции каждой от­расли.

С использованием математических методов показатели полных мате­риальных затрат могут быть рассчитаны с необходимой точностью.

Связь между валовым и конечным выпуском продукции отраслей с использованием показателей прямых материальных затрат выражается формулой (1.5):

X = (E – A)^-1 Y ,

или

X = B Y

где B = (E – A)^-1 – матрица полных материальных затрат.

В поэлементной форме X = B Y записывается в виде:

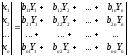(3.1)

Зная матрицы прямых и полных материальных затрат, можно найти матрицу косвенных затрат: С = В - А, где С - матрица косвенных затрат.

Матрица А, все элементы которой неотрицательны, называется продуктивной, если для любого вектора Y с неотрицательными компонентами существует решение уравнения (1.5) – векторы х, все элементы которого неотрицательны. В таком случае и модель называется продуктивной.

Существует два основных критерия продуктивности матрицы А:

1. Матрица А продуктивна тогда и только тогда, когда матрица (E – A)^-1 существует и ее элементы неотрицательны.

2. Матрица А с неотрицательными элементами продуктивна, если сумма элементов по любому ее столбцу (строке) не превосходит единицы:

,

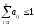причем хотя бы для одного столбца (строки) эта сумма сторого меньше единицы.

4. Использование матричной модели межотраслевого баланса

   1. Расчет полных трудовых затрат на производство продукции отраслей

Полная трудоемкость производства продукции отраслей складывается из полной трудоемкости овеществленного труда и прямых удельных затрат живого труда на производство продукции.

Расчет полных трудовых затрат на производство продукции отраслей выражается системой уравнений:

Т₁ = а₁₁ Т₁ + а_2] Т₂+ ... + а_n1 Т_n + t₁

Т₂ = а₁₂ Т₁ + а₂₂ Т₂ + … + а_n2 Т_n + t₂

……………………………………

Т_n = а_1n Т₁ + а_2n Т₂ + … + а_nn Т_n + t_n

или

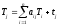(j = 1, 2, …, n) (4.1)

где a_ij - коэффициенты прямых материальных затрат продукции i-той от­расли на единицу валового выпуска продукции j-той отрасли; T_i(j) - полные затраты труда на единицу продукции i-той или j-той от­расли; t_j - прямые затраты труда на единицу валовой продукции j той отрас­ли.

В векторной форме формулу (4.1) можно представить

Т = А Т +t (4.2)

где А - матрица прямых материальных затрат с элементами a_ij (i = j = 1, 2, …, n);

Т - вектор полной трудоемкости продукции отраслей с компонентами (Т₁, Т₂, ..., Т_n);

t - вектор прямой удельной трудоемкости продукции отраслей с ком­понентами (t₁, t₂, ..., t_n).

Из (4.2) следует, что

Т = t В (4.3)

где В - матрица полных материальных затрат.

В поэлементной форме (4.3) записывается в виде:

(4.4)

Полная трудоемкость продукции каждой отрасли выступает как взве­шенная сумма произведений показателей полных материальных затрат и прямой удельной трудоемкости продукции отраслей.

2. Расчет полной капиталоемкости продукции отраслей

Полная капиталоемкость продукции отраслей складывается из прямой удельной капиталоемкости продукции отраслей и полной капитплоемкости всех материальных затрат на производство продукции данных отраслей

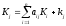(j = 1, 2, …, n) (4.5)

где a_ij - коэффициенты прямых материальных затрат продукции i-той от­расли на единицу валового выпуска продукции j-той отрасли; К_i(j) – полная капиталоемкость продукции i-той или j-той от­расли; к_j – коэффициент прямой удельной капиталоемкости продукции j-той отрас­ли.

В векторной форме формулу (4.5) можно представить

К = А К +к (4.6)

где А - матрица прямых материальных затрат с элементами a_ij (i = j = 1, 2, …, n);

К - вектор полной капиталоемкости продукции отраслей с компонентами (К₁, К₂, ..., К_n);

к - вектор прямой удельной капиталоемкости продукции отраслей с ком­понентами (к₁, к₂, ..., к_n).

Из формулы (4.6) следует, что

К = к В (4.7)

где В - матрица полных материальных затрат.

В поэлементной форме (4.7) записывается в виде:

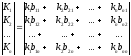(4.8)

3. Полная фондоемкость продукции отраслей

Полная фондоемкость продукции отраслей складывается из прямой удельной фондоемкости продукции отраслей и полной фондоемкости материальных затрат на производствопродукции данных отраслей.

Расчет полной фондоемкости продукции осуществляется по формуле

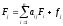(j = 1, 2, …, n) (4.9)

где a_ij - коэффициенты прямых материальных затрат продукции i-той от­расли на единицу валового выпуска продукции j-той отрасли; F_i(j) – полная фондоемкость продукции i-той или j-той от­расли;f_j - коэффициент прямой удельной фондоемкости продукции j той отрас­ли.

В векторной форме формулу (4.9) можно представить

F = А F +f (4.10)

где А - матрица прямых материальных затрат с элементами a_ij (i = j = 1, 2, …, n);

F - вектор полной фондоемкости продукции отраслей с компонентами (F₁, F₂, ..., F_n);

f - вектор прямой удельной фондоемкости продукции отраслей с ком­понентами (f₁, f₂, ..., f_n).

Из (4.10) следует, что

F = f В (4.11)

где В - матрица полных материальных затрат.

В поэлементной форме (4.11) записывается в виде:

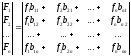(4.12)

Наряду с полной фондоемкостью продукции отраслей, рассчитываемой в среднем по всем видам фондов, можно определить полную фондоемкость продукции отраслей дифференцировано по каждому виду фондов

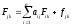(j = 1, 2, …, n) (4.13)

где a_ij - коэффициенты прямых материальных затрат продукции i-той от­расли на единицу валового выпуска продукции j-той отрасли; F_i(j)k – полная фондоемкость продукции i-той или j-той от­расли по k-тому виду фондов;f_jk - коэффициент прямой удельной фондоемкости продукции j-той отрас­ли по k-тому виду фондов.

В векторной форме формулу (4.13) можно представить

F_k = А F_k +f_k (4.14)

где А - матрица прямых материальных затрат с элементами a_ij (i = j = 1, 2, …, n);

F_k - вектор полной фондоемкости продукции отраслей по k-тому виду фондов с компонентами (F_1k, F_2k, ..., F_nk);

f_k - вектор прямой удельной фондоемкости продукции отраслей по k-тому виду фондов с ком­понентами (f_1k, f_2k, ..., f_nk).

Из (4.14) следует, что

F_k = f_k В

4. Использование матричных моделей на уровне предприятия

А. Применение матричной модели межотраслевого баланса в решении задач определения себестоимости работ, оказываемых основному производству всеми вспомогательными подразделениями

В. Определение затрат внешних ресурсов с помощью межотраслевого баланса