
- •Тема1: Оформление документа, ввод и редактирование формул. Вычислительные особенности MathСad. Операторы и математические функции. Символьные вычисления.
- •Практическая часть
- •Символьные вычисления.
- •Порядок выполнения работы
- •Контрольные вопросы.
- •Варианты заданий Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9.
- •Вариант 10
- •Тема 2. Графические возможности пакета инженерных расчетов MathCad. Анимация.
- •Среди трехмерных выделяют
- •Построение двумерного графика.
- •Построение графиков в полярных координатах
- •3. Размещение нескольких графиков на чертеже.
- •4. Форматирование двумерных графиков.
- •Изменение диапазона осей.
- •Создание маркеров.
- •Трассировка и увеличение масштаба просмотра графика.
- •5. Построение графиков поверхностей
- •6. Форматирование графика поверхности.
- •7. Анимация.
- •Средства пакета MathCad для решения нелинейных уравнений
- •Поиск корня алгебраического уравнения в заданном интервале
- •Корни полинома
- •2. Решение систем нелинейных уравнений. Метод простых итераций (последовательных приближений).
- •Средства пакета MathCad для решения нелинейных уравнений
- •Пример 4. Решить систему уравнений в окрестности точки . Выполним проверку
- •Функции MathCad для решения задач оптимизации.
- •Варианты заданий
- •Тема 4: Элементы программирования в пакете инженерных расчетов MathCad.
- •Теоретические сведения.
- •Практическая часть
Функции MathCad для решения задач оптимизации.
MathCAD с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканировать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Второй вариант таит в себе опасность уйти в окрестность другого локального экстремума, но часто может быть предпочтительнее при решении практических задач.
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
-
Minimize (f, x1, ... ,хn) – вектор значений аргументов, при которых функция f достигает минимума;
-
Maximize (f, x1, ... ,хn) – вектор значений аргументов, при которых функция f достигает максимума;
-
f(x1, ... ,хn)– заданная целевая функция;
-
x1, ... ,хn – аргументы, по которым производится минимизация(максимизация).
Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения.
Пример 7. Поиск локального экстремума в окрестности заданной точки.
Найти
максимум функции
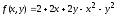 в окрестности точки (4;5).
в окрестности точки (4;5).
Ответ:
функция имеет максимум, равный 4, в
точке(1;1).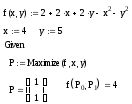
Пример 8. Поиск условного экстремума функции.
Найти
минимум функции
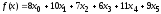 при условиях
при условиях
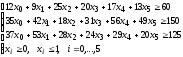 .
.
Решение.
-
Задаем целевую функцию, матрицу системы ограничений и вектор правой части этой системы

-
Задаем начальное приближение решения
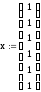
3. С помощью вычислительного блока находим минимальное значение функции и значение вектора, на котором достигается это значение.
Ответ:
минимум функции равен 32.155 и достигается
в точке (1,0.623,0.343,1,0.048,1).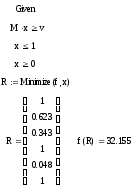
Контрольные вопросы.
-
Что значит отделить корень
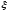 уравнения
уравнения
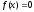 ?
?
-
Какие функции могут быть использованы для решения нелинейных уравнений?
-
Опишите конструкцию вычислительного блока.
-
В чем состоит градиентный метод?
-
В чем различие между функциями Find и Minner для решения систем нелинейных уравнений?
-
Где необходимо расположить ограничительные условия при решении задачи оптимизации?
-
Как ограничено число ограничительных условий для решения задачи оптимизации?
Варианты заданий
Вариант 1
-
Решить уравнение
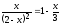 ,
используя встроенные функции root
и Find.
Сравнить полученные решения.
,
используя встроенные функции root
и Find.
Сравнить полученные решения. -
Найти все корни полинома
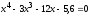 .
Проиллюстрировать решение графически.
.
Проиллюстрировать решение графически. -
Решить систему нелинейных уравнений:
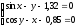
-
Найти максимум функции
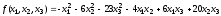 .
.
Вариант 2
-
Решить уравнение
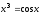 ,
,
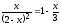 ,
используя встроенные функции root
и Find.
Сравнить полученные решения.
,
используя встроенные функции root
и Find.
Сравнить полученные решения. -
Найти все корни полинома
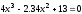 .
Проиллюстрировать решение графически.
.
Проиллюстрировать решение графически. -
Решить систему нелинейных уравнений:
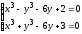 .
. -
Найти максимум функции
 при ограничении
при ограничении
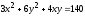 .
.
Вариант 3
-
Решить уравнение
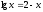 ,
,
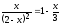 ,
используя встроенные функции root
и Find.
Сравнить полученные решения.
,
используя встроенные функции root
и Find.
Сравнить полученные решения. -
Найти все корни полинома
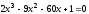 .
Проиллюстрировать решение графически.
.
Проиллюстрировать решение графически. -
Решить систему нелинейных уравнений:
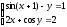 .
. -
Найти максимум функции
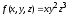 при
ограничении
при
ограничении
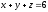 .
.
Вариант 4
-
Решить уравнение
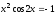 ,
,
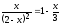 ,
используя встроенные функции root
и Find.
Сравнить полученные решения.
,
используя встроенные функции root
и Find.
Сравнить полученные решения. -
Найти все корни полинома
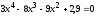 .
Проиллюстрировать решение графически.
.
Проиллюстрировать решение графически. -
Решить систему нелинейных уравнений:
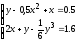 .
. -
Найти максимум функции
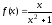 .
.
Вариант 5
-
Решить уравнение
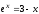 ,
,
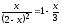 ,
используя встроенные функции root
и Find.
Сравнить полученные решения.
,
используя встроенные функции root
и Find.
Сравнить полученные решения. -
Найти все корни полинома
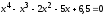 .
Проиллюстрировать решение графически.
.
Проиллюстрировать решение графически. -
Решить систему нелинейных уравнений:
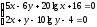 .
. -
Найти минимальное и максимальное значения функции
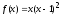 .
.
Вариант 6
-
Решить уравнение
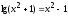 ,
,
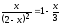 ,
используя встроенные функции root
и Find.
Сравнить полученные решения.
,
используя встроенные функции root
и Find.
Сравнить полученные решения. -
Найти все корни полинома
 .
Проиллюстрировать решение графически.
.
Проиллюстрировать решение графически. -
Решить систему нелинейных уравнений:
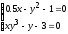 .
. -
Найти максимум функции
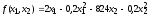 при условиях
при условиях
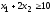 ,
,
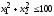 ,
,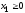
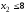 .
.
Вариант 7
-
Решить уравнение
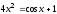 ,
,
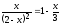 ,
используя встроенные функции root
и Find.
Сравнить полученные решения.
,
используя встроенные функции root
и Find.
Сравнить полученные решения. -
Найти все корни полинома
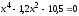 .
Проиллюстрировать решение графически.
.
Проиллюстрировать решение графически. -
Решить систему нелинейных уравнений:
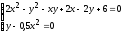 .
Выполнить
проверку.
.
Выполнить
проверку. -
Найти минимум функции
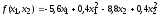 при условиях
при условиях
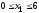 ,
,
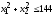 ,
,
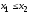 .
.
Вариант 8
-
Решить уравнение
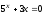 ,
,
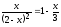 ,
используя встроенные функции root
и Find.
Сравнить полученные решения.
,
используя встроенные функции root
и Find.
Сравнить полученные решения. -
Найти все корни полинома
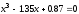 .
Проиллюстрировать решение графически.
.
Проиллюстрировать решение графически. -
Решить систему нелинейных уравнений:
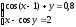 .
Выполнить
проверку.
.
Выполнить
проверку. -
Найти минимум функции
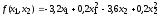 при условиях
при условиях
 ,
,
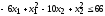 ,
,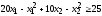 .
.
Вариант 9
-
Решить уравнение
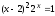 ,
,
 ,
используя встроенные функции root
и Find.
Сравнить полученные решения.
,
используя встроенные функции root
и Find.
Сравнить полученные решения. -
Найти все корни полинома
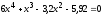 .
Проиллюстрировать решение графически.
.
Проиллюстрировать решение графически. -
Решить систему нелинейных уравнений:
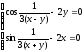 .
Выполнить
проверку
.
Выполнить
проверку -
Найти минимум функции
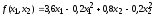 при условиях
при условиях
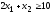 ,
,
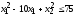 ,
,
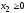 .
.
Вариант 10
-
Решить уравнение, предварительно оделив корни 7
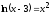 ,
,
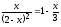 ,
используя встроенные функции root
и Find.
Сравнить полученные решения.
,
используя встроенные функции root
и Find.
Сравнить полученные решения. -
Найти все корни полинома
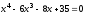 .
Проиллюстрировать решение графически.
.
Проиллюстрировать решение графически. -
Решить систему нелинейных уравнений:
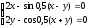 .
Выполнить проверку.
.
Выполнить проверку.
-
Найти минимум функции
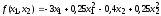 при условиях
при условиях
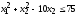 ,
,
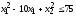 ,
,
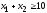 .
.
