Уравнение рисар в оригиналах

Для разомкнутой системы

сигнал ошибки (внешний сигнал) – есть сам сигнал

Если дан сигнал на входе и если известна весовая функция ПНЧ к(t), то можно найти выходной сигнал в оригинале

при

- непрерывный выходной сигнал

Если перейдем к дискретной функции t=mТ, то получим уравнение РИСАР в оригиналах

(21)

если k(t) – весовая функция ПНЧ

k(mТ) – весовая функция РИСАР

- это Д преобразование от весовой функции РИСАР

Определение уравнение зисар в оригиналах

В непрерывном варианте

в дискретном варианте

t=mT

приs>m

Уравнение ЗИСАР в оригиналах

(22)

где к – весовая функция разомкнутой системы

вспомним, что

т.е.

(23)

получили сигнал через весовую характеристику ЗИСАР

Частотные характеристики импульсных систем

Передаточные функции импульсных систем

порядок числителя на 1 меньше порядка знаменателя

в частотной области

функция трансцендентной переменной

АФХ - функция от трансцендентных переменных

Плоскость р=σ+jω ПлоскостьZ=e^jωnTПлоскостьw

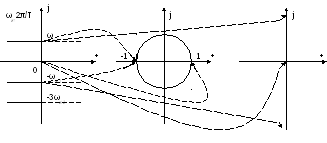
Плоскость

Плоскость

при ω=0, получим 1 при , тогда

при , тогда

Плоскость w

поскольку ;

Заменим формулой Эйлера

В плоскости

при

при

при

1. В новую переменную Zвходит алгебраически

2. Из положительной полуполосы плоскость р переходит в левую полуплоскость, плоскость - из отрицательной в правую.

3. Введем псевдочастоту

Введем размерную псевдочастоту

[1/сек]

Если изменяется отдо, тоизменяется от до .

Если ,,, тогда

Пример 1

Построить частотные характеристики для дигратора

или

Для сравнения приведем пример непрерывного интеграла

,

ω

ω=k

Построение частотных характеристик дигратора

,

,

при λ = 0, φ^* = 0

при λ = 2/Т, φ^* = π/4

при λ = ∞, φ^*=-π/2

С уменьшением периода квантования дискретный интегратор приближается к непрерывному.

Пример 2

Построим частотные характеристики дискретного аналога апериодического звена

Частотные характеристики непрерывного звена

,

к

ω=1/Т_а

;

/(1-d)

где

Получим частотные характеристики

,

при Т→0, =1

Это значит, что характеристика во втором случае стремится к нулю, а это значит, что она стремится к характеристике апериодического звена.

Заключение: Если перейти к новой переменной λ,то проблемы при построении частотных характеристик снимаются. Их можно строить также, как и при переменной ω.

Устойчивость импульсных систем

- при непрерывных системах

Для импульсных систем

на устойчивость системы влияет поведение

с течением времени свободная составляющая стремиться к нулю

У (система устойчива)

с течением времени свободная составляющая стремиться к бесконечности

(система не устойчива)

гр. У

Импульсная система будет устойчивой, если корни характеристического уравнения – левые.

корни должны быть левые

Корни ПНЧ совпадают с корнями разомкнутой системы.

Отсюда следует, что РИСАР устойчива, неустойчива или нейтральна, если устойчива, неустойчива или нейтральна ее ПНЧ.

Характеристическое уравнение ИСАР имеет вид

Для замкнутой системы корни ПНЧ не совпадают с корнями импульсной системы, поэтому вводят переменную

обозначим

умножим на

Если составим матрицу Гурвица, то система устойчива, когда все миноры одного знака

Для непрерывных систем

,

Для импульсных систем

умножим на (1-w)

при n=1

по Гурвицу

при n=2

для непрерывных систем

,,

для импульсных систем

умножим на

по Гурвицу

Пример

,,