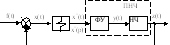Импульсный элемент и его уравнение

Амплитудно – импульсный элемент– устройство, реагирующее на дискретные равноотстоящие друг от друга значения входного сигналаx(t) приt=mT, а выходной величиной является последовательность импульсов определенной формыS(t), амплитуды которых пропорциональны дискретным значениям входной величиныx(mT).

Реальный импульсный элемент заменяют виртуальной совокупностью двух устройств: простейшего импульсного элемента (ПИЭ) и формирующего устройства (ФУ).

Простейший импульсный элемент (ПИЭ) – элемент, выходной величиной которого x^*(t) представляет собой модулированную последовательность дельта – функции, площади которых равны дискретным значениям входной величиныx(mT). Дельта функция равна 1 везде.

Задача формирующего устройства (ФУ)состоит в том, чтобы из входной последовательности модулированных дельта импульсов, которые дает простейший исполнительный элемент сформировать такие же формы импульсов, что и для реального исполнительного элемента.

S(t) =

Передаточная функция ФУ для прямоугольных импульсов (непрерывная функция)

Менять местами ПИЭ и ПНЧ нельзя.

ПИЭ – это устройство, на вход которого поступает непрерывный сигнал, а на выходе получается модулированная последовательность дельта (δ) – импульсов.

Рассмотрим немодулированную последовательность дельта (δ) – импульсов

(1)

δ(t) =

Длительность этого импульса стремится к нулю, амплитуда - к бесконечности, а площадь равна 1. По высоте импульса откладывается площадь.

Модуляция означает, что каждый из импульсов имеет площадь, отвечающую величине дискреты и соответствующему моменту квантования.

(2)

Сигнал на выходе простейшего элемента означает умножение последовательности немодулированных импульсов на входной сигнал

.

Формула изображения для входного сигнала.

Это обычное преобразование Лапласа для входной непрерывной функции x(t).

Найдем необычное преобразование Лапласа для входной величины x(t):

Подставим вместо уравнение (1), получим

Интеграл равен значению подынтегральной функции при аргументе равном нулю.

(4)

Формула (4) – это формула дискретного или Д- преобразования Лапласа.

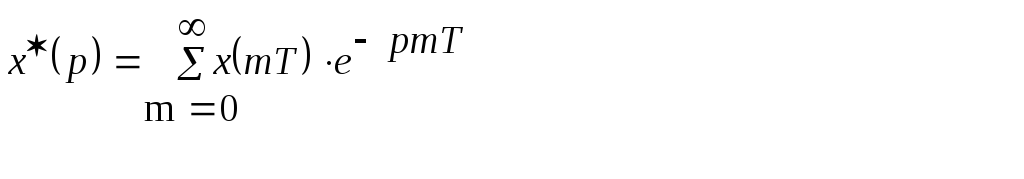4а)

Дискретное преобразование Лапласа – это бесконечный ряд, ряд должен сходиться. Ряд сходится, если действительная часть больше некоторой постоянной с.

(5)

Определим спектр дискретного сигнала на выходе простейшего импульсного элемента.

(6)

Если , то выражение (4а) получится

(7)

Выражение (7) – это Z– преобразование Лапласа.

Выражение (7) - алгебраическое, оно удобнее, чем Д – преобразование (трансцендентное).

Сигнал на выходе периодичен с периодом, обусловленным частотой квантования (это значит, что спектр повторяется бесчисленное количество раз).

Отсюда видно, что спектр на выходе ПИЭ периодичен вдоль оси частот.

Изображение сигнала периодично вдоль оси частот с периодом, обусловленным частотой квантования.

Значение отрицательного спектра симметрично положительному, поэтому рассматривают только полуполосу для положительных частот.

Найдем связь между спектром и изображениями входного и выходного сигналов ПИЭ, т.е. непрерывной и дискретной функцией.

Сигнал на входе ПИЭ:

Это обычное преобразование Лапласа от модулированной последовательности δ – импульсов.

Изображение x(p) есть Лапласово преобразование.

Выражение (8) – это - преобразование Лапласа. Оно справедливо в том случае, когда

Выражение (8а) – изображение сигнала на выходе ПИЭ.

Выражение (9) - обычное преобразование Лапласа .

Передаточной функции простейшего импульсного элемента не существует.

Подставим в формулы (8) и (8а), получим

Составляющие прииз (10) и (10а) называются транспонированными составляющими.

Положим, что .

Спектр состоит из действительной и мнимой части. Соотношение спектров на выходе и входе ПИЭ можно изучать из действительной и мнимой частей.

Пусть действительная часть спектра входного сигнала имеет симметричный вид.

1. Спектр на выходе периодичен с частотой .

2. Спектр выходного сигнала отличается от входного не только в области высоких, но и в области низких частот за счет хвостов транспонированных составляющих. За счет накладывания хвостов происходит искажение холмов спектров.

По изображению выходного сигнала нельзя восстановить входной, т.к. выходной сигнал – это решетчатая функция. Информация между дискретами сигнала теряется. Однако, при некоторых условиях можно из выходного сигнала восстановить входной. Это возможно при выполнении условий теоремы Котельникова.

2условия теоремы Котельникова:

1. Спектр входного сигнала должен быть финитен или конечен, т.е.

2. Частота квантования должна быть не меньше удвоенной граничной частоты

При выполнении этих двух условий получается, что можно восстановить входной сигнал из выходного.

ФУ – формирующее устройство

НЧ – непрерывная часть

ПНЧ – приведенная непрерывная часть