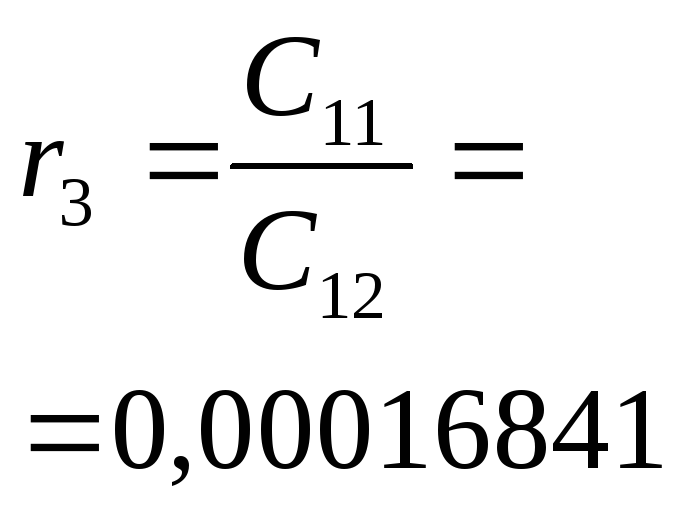16

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖИНЕРО – СТРОИТЕЛЬНЫЙ

КАФЕДРА УПРАВЛЕНИЯ И ИНФОРМАТИКИ В ТЕХНИЧЕСКИХ СИСТЕМАХ

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1

по дисциплине ТАУ.

 ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ

ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Выполнили ст. гр. УИТ-41

Данилова В.А.

Принял доцент каф. УИТ

Скоробогатова Т.Н._______

«___»_______________2003

2003

СОДЕРЖАНИЕ

Задание 3

1 Преобразование структурной схемы САР 4

2 Критерии устойчивости 6

2.1 Критерий Гурвица 6

2.2 Критерий Льенара-Шипара 7

2.3 Критерий Рауса 7

2.4 Критерий Найквиста 8

2.5 Критерий Михайлова 10

2.6 D-разбиение 12

2.7 Устойчивость системы по методу Ляпунова 14

Вариант №55

Дана структурная схема САР вида рисунка 1, с передаточными функциями звеньев: , , , , , . Необходимо проверить устойчивость системы по критериям: Гурвица, Льенара – Шипара, Рауса, Михайлова, Найквиста, D-разбиения, Ляпунова, Шур - Кона.

Рисунок 1

1 ПРЕОБРАЗОВАНИЕ СТРУКТУРНОЙ СХЕМЫ САР

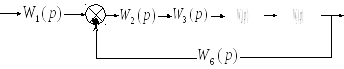
Рисунок 2

Звенья W₂(p), W₃(p), W₄(p), W₅(p) соединены последовательно, следовательно, имеем:

,

.

В соответствии с данным преобразованием, структурная схема САУ примет вид:

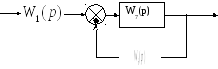
Рисунок 3

Звенья W₆(p), W₇(p) включены встречно – параллельно, следовательно:

,

.

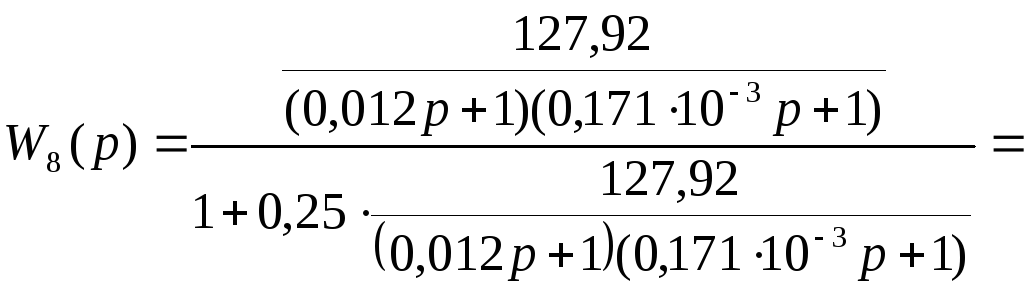
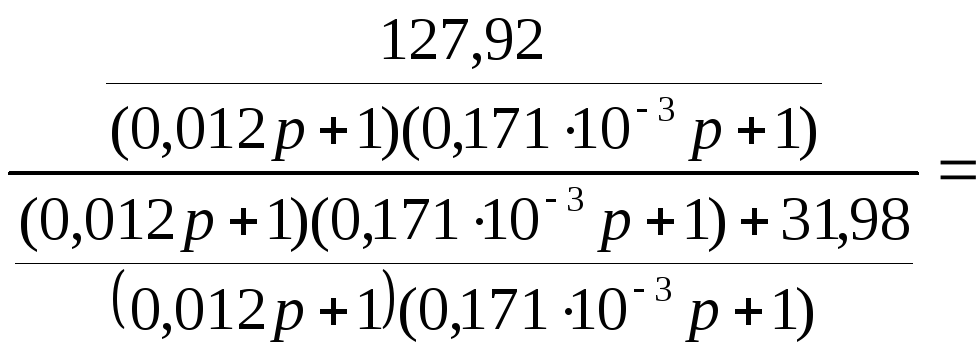
Тогда:

Рисунок 4

Исходя из схемы рисунка 4, по правилу преобразования структурных схем, получим передаточную функцию системы:

,

.

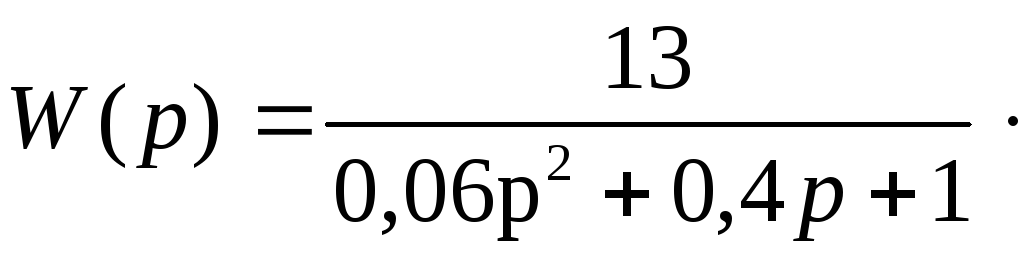
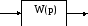Получим:

Рисунок 5

Т.е. передаточная функция системы имеет вид:

.

2 КРИТЕРИИ УСТОЙЧИВОСТИ

Запишем характеристическое уравнение для рассматриваемой системы, получим:

.

Характеристическое уравнение является уравнением 4-го порядка, коэффициенты которого положительны, а значит и корни все левые, из чего можно сделать вывод, что необходимое условие устойчивости выполняется.

2.1 КРИТЕРИЙ ГУРВИЦА

Составим определители Гурвица из коэффициентов характеристического уравнения:;;;; .

=0,63;

=0,019;

;

.

Согласно критерию Гурвица, система устойчива, т.к. определители имеют одинаковые знаки с коэффициентом .

2.2 КРИТЕРИЙ ЛЬЕНАРА – ШИПАРА

Данная нам система является устойчивой, т.к. при положительности коэффициентов , , , , характеристического уравнения все определители Гурвица с нечетным индексом положительны.

Таким образом, условие устойчивости можно записать следующим образом:

; .

2.3 КРИТЕРИЙ РАУСА

Устойчивость системы по критерию Рауса определяется из таблицы, элементами которой являются коэффициенты, вычисляемые по следующим формулам:

; .

Таблица 1

Коэффициент	Номер строки i	Номер столбца к
		к=1	к=2	к=3
-	1	a0=C11	a2=C21	a4=C31
-	2	a1=C12	a3=C22	a5=C32=0
	3
	4
	5
	6

Данная нам система является устойчивой, т.к. коэффициент a₀, а также все коэффициенты первого столбца таблицы Рауса являются положительными.

2.4 КРИТЕРИЙ НАЙКВИСТА

Если СУ устойчива в разомкнутом состоянии, то для того, чтобы она была устойчива в замкнутом, необходимо и достаточно, чтобы кривая АФЧХ разомкнутой системы при изменении от 0 до не будет охватывать точку .

Представим передаточную функцию в комплексной форме, т.е. .

.

Получим действительную и мнимую части:

;

.

;

;

Построим кривую, но сначала проведем следующий анализ:

;

.

Получим:

Рисунок 6

По условию устойчивости Найквиста, кривая не должна охватывать точку , увеличим масштаб рисунка 6 для большей наглядности.

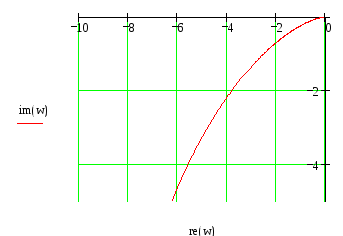
Рисунок 7

Из рисунка 7 видно, что данная нам система устойчива.

2.5 КРИТЕРИЙ МИХАЙЛОВА

Согласно данному критерию для того, чтобы САУ была устойчивой необходимо и достаточно, чтобы вектор кривой Михайлова при изменении частоты от 0 до , повернулся в положительном направлении вокруг начала координат на угол , где - порядок характеристического уравнения.

Характеристическое уравнение рассматриваемой системы имеет вид:

Заменим на , получим:

Представим характеристический полином в виде:

;

;

.

;

Построим кривую Михайлова, но сначала проведем следующий анализ:

;

;

.

Графики построены с постепенным увеличением масштаба, т.е.:

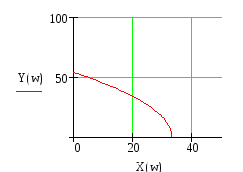
Рисунок 8,а

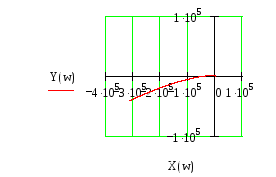
Рисунок 8,б

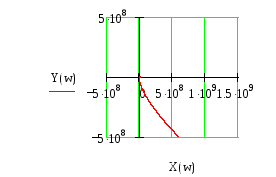
Рисунок 8, в

Из рисунка 8,в видно, что вектор кривой Михайлова поворачивается на угол , т.е. уходит в бесконечность в 4 квадранте, следовательно, система устойчива.

2.6 D-РАЗБИЕНИЕ

Выполним D-разбиение по одному параметру.

Пусть , тогда передаточная функция системы примет вид:

.

Охватим всю систему обратной отрицательной связью, т.е.:

Рисунок 9

Следовательно, общая передаточная функция вычисляется по формуле:

;

.

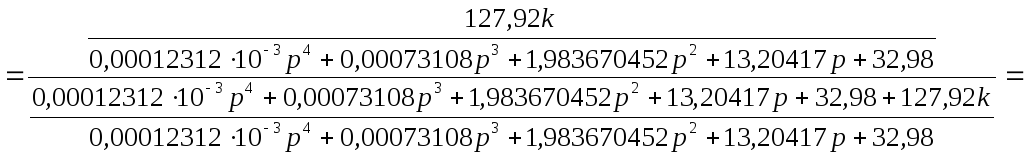
Т.е.:

.

Тогда характеристическое уравнение имеет вид:

.

В последнем выражении произведем замену и выразим из него коэффициент k:

;

.

Выразим действительную и мнимую части, а затем построим кривую D – разбиения по параметру k.

( k )

( k )

D(0)

D(1)

D(1)

№1

№2

Рисунок 10

Переходу по стрелке №1 соответствует уменьшение правых корней на единицу, переходу по стрелке №2 соответствует уменьшение правых корней на единицу. В результате переходов попадаем в область, где число правых корней минимально, т.е. в область D(o).

Область D(o) является областью подозрительной на область устойчивости, и требует проверки.

Выберем из области D(o) произвольное значение параметра k, например k=100, и подставим в характеристическое уравнение, получим:

.

Выполним проверку устойчивости по критерию Гурвица.

Составим определители Гурвица из коэффициентов характеристического уравнения:;;;; .

=23,66;

=0,018;

;

.

Так как определители положительны при положительном а₀, то САУ является устойчивой.

2.7 УСТОЙЧИВОСТЬ СИСТЕМЫ ПО МЕТОДУ ЛЯПУНОВА

По критерию устойчивости Ляпунова, система устойчива, если для нее выполняется следующее условие: .

Т.е. для того чтобы САУ была устойчива необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части.

.

Определим корни характеристического уравнения:

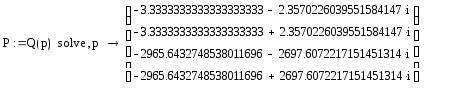
Так как все корни характеристического уравнения лежат с лева от мнимой оси (левые корни) и имеют отрицательную вещественную часть, то САУ будет устойчивой.