лабораторная работа / Практические / Практическая работа00

Практическая работа №1.

Задание:

Задана структурная схема САУ вида:

Требуется упростить вышеприведенную схему САУ и проверить заданную САУ на устойчивость по 8 критериям.

Заменим два звена с передаточными функциями W₁(p) и W₂(p), соединенных параллельно, одним звеном с передаточной функцией:

Теперь заменим два звена с передаточными функциями W^/(p) и W₃(p), соединенных последовательно, одним звеном. Передаточная функция этого звена и будет являться передаточной функцией разомкнутой САУ:

.

Для получения передаточной функции замкнутой САУ, замкнем САУ отрицательной обратной связью, тогда схема примет вид:

Передаточная функция замкнутой системы определится следующим образом:

Подставим в [1] и [2] заданные значения передаточных функций.

1. Проверка устойчивости по Гурвицу.

Для того чтобы САУ была устойчива необходимо и достаточно, чтобы все определители Гурвица имели одинаковый знак с коэффициентом а₀, а при a₀>0 – были положительными. Определители составляются из коэффициентов характеристического уравнения. Составим характеристическое уравнение для заданной САУ.

По определению передаточной функции:

Уравнение [3] и является характеристическим уравнением для заданной системы.

Составим главный определитель Гурвица.

Частный определитель Гурвица:

Так как определители положительны при положительном а₀, то САУ является устойчивой.

2. Проверка устойчивости по Льенеру-Шипару.

Для того чтобы САУ была устойчива необходимо и достаточно, чтобы при положительных коэффициентах характеристического уравнения все определители с четными(нечетными) индексами были положительными.

Все условия выполняются – система устойчива.

3. Проверка устойчивости по Раусу.

Для того чтобы САУ была устойчива необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы Рауса имели одинаковый знак с а₀, а при а₀>0 были положительными. Таблица Рауса составляется из коэффициентов характеристического уравнения, которые располагаются в таблице по строкам и столбцам. В 1 строке записываются коэффициенты с четными индексами, а во второй – с нечетными. Все остальные клетки таблицы заполняются коэффициентами, которые вычисляются так:

k – номер столбца в таблице, i – номер строки.

Составим таблицу Рауса для нашей системы.

Таблица 1.

	Номер строки – i.	Номер столбца – k.
		k=1	k=2
-	1
-	2
	3
	4

Из таблицы видно, что все коэффициенты положительны, значит САУ – устойчива.

4. Проверка устойчивости по Ляпунову.

Для того чтобы САУ была устойчива необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части.

Из передаточной функции замкнутой системы определим характеристическое уравнение.

Определим корни характеристического уравнения.

Так как оба корня характеристического уравнения имеют отрицательную вещественную часть, то САУ будет устойчивой.

5. Проверка устойчивости по Михайлову.

Для того чтобы САУ была устойчива необходимо и достаточно, чтобы кривая Михайлова, проходила последовательно, нигде не обращаясь в 0, n квадрантов, где n – порядок характеристического уравнения.

Построим кривую Михайлова для нашей системы.

В характеристическом уравнении заменим р на jw.

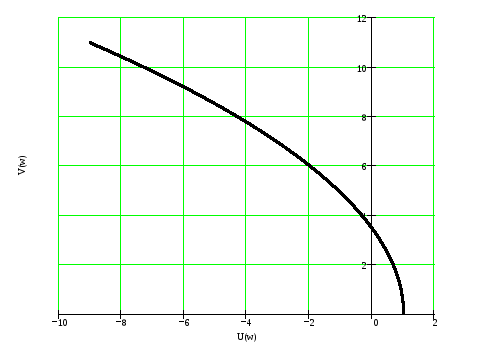
Так как порядок характеристического уравнения равен 2, а кривая Михайлова, начинаясь на вещественной полуоси, проходит последовательно 2 квадранта, то САУ будет устойчивой.

6. Проверка устойчивости по Найквисту.

Разомкнутая САУ будет устойчивой, если кривая АФЧХ замкнутой системы, имеющей m полюсов в правой полуплоскости, при увеличении от 0 до не будет охватывать точку .

Для нашей САУ, передаточная функция замкнутой системы равна:

Выразим действительную и мнимую части и построим график.

7. Проверка устойчивости по принципу D – разбиения.

Выполним D-разбиение по 1 параметру.

Запишем характеристическое уравнение и выразим из него коэффициент а₂.

В последнем выражении заменим р на jw и выразим действительную и мнимую части. Затем построим кривую D – разбиения.

D(0)

D(1)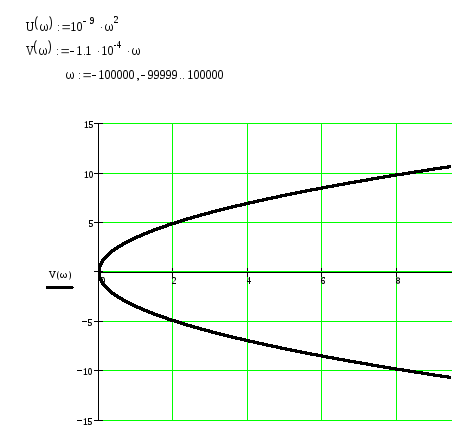

Из графика видно, что область D(0), является областью подозрительной на устойчивость. Проверим это. Пусть a₂=0,5, тогда характеристическое уравнение примет вид:

Решая это уравнение, получаем, что:

так как все корни имеют отрицательную вещественную часть, то по Ляпунову САУ будет устойчивой, а это значит, что область D(0), является областью устойчивости системы по параметру a₂.

8. Проверка устойчивости по Шур - Кону.

Для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы определители Шур - Кона с нечетными индексами были меньше 0, а – с четными индексами были больше 0.

Передаточная функция для замкнутого состояния САУ имеет вид:

Запишем эту передаточную функцию в форме z-преобразований, для этого из таблицы соответствий воспользуемся формулой:

Тогда z- преобразование для передаточной функции для замкнутого состояния САУ запишется следующим образом:

Характеристическое уравнение замкнутой САУ в форме z-преобразований имеет вид:

Определитель Шур - Кона имеет вид:

Составим и вычислим четные и нечетные определители Шур-Кона.

_Δ2>0

Так как четные определители больше 0, а нечетные меньше 0, то САУ будет устойчивой.

					Практическая работа №1. Copyright © by Рызлейцев Александр Александрович, УИТ-43
				15.07		12
Изм	Лист.	№ докум.	Подп	Дата