Алгоритм

Пусть требуется найти безусловный минимум функции n переменных . Предполагается, что серьёзных ограничений на область определения функции нет, то есть функция определена во всех встречающихся точках.

Параметрами метода являются:

• коэффициент отражения α > 0, обычно выбирается равным 1.

• коэффициент сжатия β > 0, обычно выбирается равным 0,5.

• коэффициент растяжения γ > 0, обычно выбирается равным 2.

Подготовка. Вначале выбирается n + 1 точка , образующие симплекс n-мерного пространства. В этих точках вычисляются значения функции: .

Дальнейший план действий:

1. Сортировка. Из вершин симплекса выбираем три точки: x_h с наибольшим (из выбранных) значением функции f_h, x_g со следующим по величине значением f_g и x_l с наименьшим значением функции f_l. Целью дальнейших манипуляций будет уменьшение по крайней мере f_h.

2. Найдём центр тяжести всех точек, за исключением x_h: 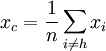. Вычислять f_c = f(x_c) не обязательно.

3. Отражение. Отразим точку x_h относительно x_c с коэффициентом α (при α = 1 это будет центральная симметрия, в общем случае — гомотетия), получим точку x_r и вычислим в ней функцию: f_r = f(x_r). Координаты новой точки вычисляются по формуле:

x_r = (1 + α)x_c − αx_h

4. Далее смотрим, насколько нам удалось уменьшить функцию, ищем место f_r в ряду f_h,f_g,f_l:

4а Если f_r < f_l, то направление выбрано удачное и можно попробовать увеличить шаг — производим растяжение. Новая точка x_e = (1 − γ)x_c + γx_r и значение функции f_e = f(x_e).

• Если f_e < f_l, то можно расширить симплекс до этой точки: заменяем точку x_l на x_e и заканчиваем итерацию (на шаг 8).

Если f_e > f_l, то переместились слишком далеко: в набор берём x_r (опять вместо x_l) и заканчиваем итерацию (на шаг 8).

4b Если f_l < f_r < f_g, то выбор точки уже неплохой (новая лучше двух прежних). Заменяем точку x_h на x_r и переходим на шаг 8.

4с Если f_h > f_r > f_g, то меняем обозначения x_r,x_h (и соответствующие значения функции) местами и идём на шаг 5.

4d Если f_r > f_h, то просто идём на следующий шаг 5.

В результате (возможно, после переобозначения) f_r > f_h > f_g > f_l.

5. Сжатие. Строим точку x_s = βx_h + (1 − β)x_c и вычисляем в ней значение f_s.

6 Если f_s < f_h, то заменяем точку x_h на x_s и идём на шаг 8.

7 Если f_s > f_h, то первоначальные точки оказались самыми маленькими. Делаем глобальное сжатие симплекса — гомотетию к точке с наименьшим значением x_l:

для всех требуемых точек x_i.

8 Последний шаг — проверка сходимости. Может выполняться по-разному, например, оценкой дисперсии набора точек. Суть проверки заключается в том, чтобы проверить взаимную близость полученных вершин симплекса, что предполагает и близость их к искомому минимуму. Если требуемая точность ещё не достигнута, можно продолжить итерации с шага 1.

Пример задачки на симплекс-метод

Рассмотрим простой пример решения задачки с помощью симплекс-метода для запоминания последовательности действий.

Некая компания производит большие и маленькие садовые скамейки. Каждая скамейка должна быть построена и отполирована. На постройку маленькой скамейки уходит 2 часа, на полировку 3 часа. На постройку большой уходит 4 часа, на полировку 3 часа. Строительный цех работает 100 часов в неделю, а полировочный 90. Прибыль, получаемая с маленькой скамейки составляет 5$, а с большой 7$. Сколько скамеек каждого вида должна производить компания для максимизации прибыли?

Пусть фирма производит X маленьких и Y больших скамеек. Тогда для решения задачи необходимо найти такие X и Y, что:

5X + 7Y - > max 2X + 4Y < = 100 3X + 3Y < = 90, X , Y > = 0

Введем переменные S1, S2 >= 0, тогда задача примет стандартный (канонический) вид: 5X + 7Y +0S1 + 0S2 - > max 2X + 4Y +1S1 + 0S2 = 100 3X + 3Y +0S1 + 1S2 = 90, X , Y, S1, S2 > = 0

Рассмотрим решение этой задачи, используя симплекс таблицу. Данное решение подходит для всех случаев, когда правая часть уравнений ограничений неотрицательна (90 и 100 в нашем примере). Если правая честь уравнений ограничений, после приведения задачи к каноническому виду, содержит отрицательные числа, то используйте вариант решения, разобранный во втором примере.

Составим симплекс-таблицу:

1 шаг: В строке Cj выписываем коэффициенты целевой функции при переменных X, Y, S1, S2. В строках 1,2 - коэффициенты при соответсвующих переменных из уравнений ограничений. RHS (столбец right hand side :-) ) , в строках 1, 2 пишем числа 100 и 90 из правой части неравенств ограничений. Переменные, образующие единичную матрицу будем называть базисными, в данном случае S1 и S2.

2 шаг: Заполняем столбец CB строки 1, 2 коэффициентами целевой функции при базисных переменных, то есть 0 при S1 в строке 1 (пересечение строки 1 и столбца S1) и 0 при S2 в строке 2.

3 шаг: заполняем строку 3 (Zj) путем перемножения каждого элемента столбца CB на соответствующие элементы строк 1, 2 и сложением. То есть первый элемент строки Zj получается как: 0*2 + 0*3 = 0. В данном случае все элементы строки получаются равными 0. Аналогично получается 0 в столбце RHS.

4 шаг: строка 4 (Cj - Zj) получается почленным вычитанием элементов строки 3 (Zj) из элементов строки Cj (всегда из верхней строки на всех шагах).

5 шаг: Ищем в строке 4 (Cj - Zj) МАКСИМАЛЬНЫЙ СТРОГОПОЛОЖИТЕЛЬНЫЙ элемент. Ему соответствует ведущий стролбец. В данном случае, в строке 4 выбираем элемент 7, следовательно ведущим будет столбец Y (строки 1,2).

6 шаг: Ищем в ведущем столбце МИНИМАЛЬНО ПОЛОЖИТЕЛЬНОЕ число из формулы (RHS/ведущий столбец). То есть, в данном случае, выбираем между 100/4=25 и 90/3=30. Найдя такое число, определяем ведущую строку, у нас строка 1. Пересечение ведущих столбца и строки дает нам ведущий элемент, в нашем случае 4.

7 шаг: Формируем строки 5, 6 путем деления ведущей строки на ведущий элемент и формирования единичного столбца на месте ведущего). Не забываем RHS. Далее следуем на шаг 2.

Итерации продолжаются до тех пор, пока в строке (Cj - Zj) не останется положительных элементов (в случае, что оптимальное решение задачи существует).

Тогда в строке Zj (у нас строка 11) в RHS - столбце получим значение целевой функции в оптимальной точке (X, Y) = (10, 20). Значения 10 и 20 получаем из RHS в строках 9, 10.