Не путать с «симплекс-методом» — методом оптимизации произвольной функции. См. Метод Нелдера — Мида

Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Метод был разработан американским математиком Джорджем Данцигом (George Dantzig) в 1947 году.

Содержание [убрать] 1 Описание 2 Алгоритм симплекс-метода 2.1 Усиленная постановка задачи 2.2 Алгоритм 3 Двухфазный симплекс-метод 3.1 Причины использования 3.2 Модификация ограничений 3.2.1 Различия между дополнительными и вспомогательными переменными 3.3 Фазы решения 4 Модифицированный симплекс-метод 5 Двойственный симплекс-метод 6 Литература

[править] Описание

Переход от одной вершины к другой

Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.

Заметим, что каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый также полиэдральным конусом. Уравнение W(x) = c, где W(x) — максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку — требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Заметим, что пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину, причём, их будет более одной, если пересечение содержит ребро или k-мерную грань. Поэтому максимум функционала можно искать в вершинах многогранника. Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.

Последовательность вычислений симплекс-методом можно разделить на две основные фазы:

1. нахождение исходной вершины множества допустимых решений,

2. последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.

При этом в некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно является допустимым решением, хотя и, скорее всего, далеко не самым оптимальным). В таких задачах первую фазу симплекс-метода можно вообще не проводить. Симплекс-метод, соответственно, делится на однофазный и двухфазный.

[править] Алгоритм симплекс-метода

[править] Усиленная постановка задачи

Рассмотрим следующую задачу линейного программирования:

Теперь поставим эту задачу в эквивалентной усиленной форме. Необходимо максимизировать Z, где:

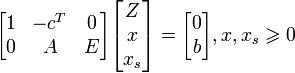
Здесь x — переменные из исходного линейного функционала, x_s — новые переменные, дополняющие старые таким образом, что неравенство переходит в равенство, c — коэффициенты исходного линейного функционала, Z — переменная, которую необходимо максимизировать. Полупространства и в пересечении образуют многогранник, представляющий множество допустимых решений. Разница между числом переменных и уравнений даёт нам число степеней свободы. Проще говоря, если мы рассматриваем вершину многогранника, то это число рёбер, по которым мы можем продолжать движение. Тогда мы можем присвоить этому числу переменных значение 0 и назвать их «непростыми». Остальные переменные при этом будут вычисляться однозначно и называться «простыми». Полученная точка будет вершиной в пересечении соответствующих непростым переменным гиперплоскостей. Для того, чтобы найти т. н. начальное допустимое решение (вершину, из которой мы начнём движение), присвоим всем изначальным переменным x значение 0 и будем их считать непростыми, а все новые будем считать простыми. При этом начальное допустимое решение вычисляется однозначно : .

[править] Алгоритм

Теперь приведём шаги алгоритма. На каждом шаге мы будем менять множества простых и непростых векторов (двигаться по рёбрам), и матрица будет иметь следующий вид:

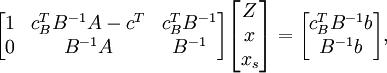
где c_B — коэффициенты вектора c соответствующие простым переменным (переменным x_s соответствуют 0), B — столбцы , соответствующие простым переменным. Матрицу, образованную оставшимися столбцами обозначим D. Почему матрица будет иметь такой вид поясним в описании шагов алгоритма.

Первый шаг.

Выбираем начальное допустимое значение, как указано выше. На первом шаге B — единичная матрица, так как простыми переменными являются x_s. c_B — нулевой вектор по тем же причинам.

Второй шаг

Покажем, что в выражении только непростые переменные имеют ненулевой коэффициент. Заметим, что из выражения Ax+x_s=b простые переменные однозначно выражаются через непростые, так как число простых переменных равно числу уравнений. Пусть x ' — простые, а x ' ' — непростые переменные на данной итерации. Уравнение Ax+x_s=b можно переписать, как Bx '+Dx ' '=b. Умножим его на B ^{− 1} слева: x' + B ^{− 1}Dx'' = B ^{− 1}b. Таким образом мы выразили простые переменные через непростые, и в выражении B ^{− 1}Ax + B ^{− 1}x_s, эквивалентному левой части равенства, все простые переменные имеют единичные коэффициенты. Поэтому, если прибавить к равенству Z − c^Tx = 0 равенство , то в полученном равенстве все простые переменные будут иметь нулевой коэффициент — все простые переменные вида x сократятся, а простые переменные вида x_s не войдут в выражение .

Выберем ребро, по которому мы будем перемещаться. Поскольку мы хотим максимизировать Z, то необходимо выбрать переменную, которая будет более всех уменьшать выражение

.

Для этого выберем переменную, которая имеет наибольший по модулю отрицательный коэффициент. Если таких переменных нет, то есть все коэффициенты этого выражения неотрицательны, то мы пришли в искомую вершину и нашли оптимальное решение. В противном случае начнём увеличивать эту непростую переменную, то есть перемещаться по соответствующему ей ребру. Эту переменную назовём входящей.

Третий шаг

Теперь необходимо понять, какая простая переменная первой обратится в ноль по мере увеличения входящей переменной. Для этого достаточно рассмотреть систему:

При фиксированных значениях непростых переменных система однозначно разрешима относительно простых, поэтому мы можем определить, какая из простых переменных первой достигнет нуля при увеличении входящей. Эту переменную назовем выходящей. Это будет означать, что мы натолкнулись на новую вершину. Теперь входящую и выходящую переменную поменяем местами — входящая «войдёт» в простую, а выходящая из них «выйдет» в непростые. Теперь перепишем матрицу B и вектор c_B в соответствии с новыми наборами простых и непростых переменных, после чего вернёмся ко второму шагу. x''

Поскольку число вершин конечно, то алгоритм однажды закончится. Найденная вершина будет являться оптимальным решением.

[править] Двухфазный симплекс-метод

[править] Причины использования

Если в условии задачи линейного программирования не все ограничения представлены неравенствами типа «≤», то далеко не всегда нулевой вектор будет допустимым решением. Однако каждая итерация симплекс-метода является переходом от одной вершины к другой, и если неизвестно ни одной вершины, алгоритм вообще не может быть начат.

Процесс нахождения исходной вершины не сильно отличается от однофазного симплекс-метода, однако может в итоге оказаться сложнее, чем дальнейшая оптимизация.

[править] Модификация ограничений

Все ограничения задачи модифицируются согласно следующим правилам:

• ограничения типа «≤» переводятся на равенства созданием дополнительной переменной с коэффициентом «+1». Эта модификация проводится и в однофазном симплекс-методе, дополнительные переменные в дальнейшем используются как исходный базис.

• ограничения типа «≥» дополняются одной переменной с коэффициентом «−1». Поскольку такая переменная из-за отрицательного коэффициента не может быть использована в исходном базисе, необходимо создать ещё одну, вспомогательную, переменную. Вспомогательные переменные всегда создаются с коэффициентом «+1».

• ограничения типа «=» дополняются одной вспомогательной переменной.

Соответственно, будет создано некоторое количество дополнительных и вспомогательных переменных. В исходный базис выбираются дополнительные переменные с коэффициентом «+1» и все вспомогательные. Осторожно: решение, которому соответствует этот базис, не является допустимым.

[править] Различия между дополнительными и вспомогательными переменными

Несмотря на то, что и дополнительные, и вспомогательные переменные создаются искусственно и используются для создания исходного базиса, их значения в решении сильно отличаются:

• дополнительные переменные сообщают, насколько соответствующее им ограничение «недоиспользовано». Значение дополнительной переменной нулю соответствует равенству значений правых и левых частей ограничения.

• вспомогательные переменные сообщают, насколько данное условие далеко от допустимого (относительно конкретного ограничения). Если значение вспомогательной переменной больше нуля, то данное решение не выполняет определённое ограничение, а значит не является допустимым.

То есть ненулевое значение дополнительной переменной может (но не должно) сигнализировать о неоптимальности решения. Ненулевое значение вспомогательной переменной сигнализирует о недопустимости решения.

[править] Фазы решения

После того, как было модифицировано условие, создаётся вспомогательная целевая функция. Если вспомогательные переменные были обозначены, как y_i, i∈{1, .., k}, то вспомогательную функцию определим, как

.

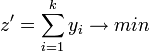После этого проводится обыкновенный симплекс-метод относительно вспомогательной целевой функции. Поскольку все вспомогательные переменные увеличивают значение z', в ходе алгоритма они будут поочерёдно выводится из базиса, при этом после каждого перехода новое решение будет всё ближе к множеству допустимых решений.

Когда будет найдено оптимальное значение вспомогательной целевой функции, могут возникнуть две ситуации:

• оптимальное значение z' больше нуля. Это значит, что как минимум одна из вспомогательных переменных осталась в базисе. В таком случае можно сделать вывод, что допустимых решений данной задачи линейного программирования не существует.

• оптимальное значение z' равно нулю. Это означает, что все вспомогательные переменные были выведены из базиса, и текущее решение является допустимым.

Во втором случае мы имеем допустимый базис, или, иначе говоря, исходное допустимое решение. Можно проводить дальнейшую оптимизацию с учётом исходной целевой функции, при этом уже не обращая внимания на вспомогательные переменные. Это и явлется второй фазой решения.

Не путать с «симплекс-методом» из линейного программирования — методом оптимизации линейной системы с ограничениями.

Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной (точнее — градиентов) функции, а поэтому легко применим к негладким функциям.

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.

Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс. Более развитый подход к исключению локальных экстремумов предлагается в генетическом методе отжига.

[править] Алгоритм

Пусть требуется найти безусловный минимум функции n переменных . Предполагается, что серьёзных ограничений на область определения функции нет, то есть функция определена во всех встречающихся точках.

Параметрами метода являются:

• коэффициент отражения α > 0, обычно выбирается равным 1.

• коэффициент сжатия β > 0, обычно выбирается равным 0,5.

• коэффициент растяжения γ > 0, обычно выбирается равным 2.

Подготовка. Вначале выбирается n + 1 точка , образующие симплекс n-мерного пространства. В этих точках вычисляются значения функции: .

Дальнейший план действий:

1. Сортировка. Из вершин симплекса выбираем три точки: x_h с наибольшим (из выбранных) значением функции f_h, x_g со следующим по величине значением f_g и x_l с наименьшим значением функции f_l. Целью дальнейших манипуляций будет уменьшение по крайней мере f_h.

2. Найдём центр тяжести всех точек, за исключением x_h: 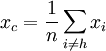. Вычислять f_c = f(x_c) не обязательно.

3. Отражение. Отразим точку x_h относительно x_c с коэффициентом α (при α = 1 это будет центральная симметрия, в общем случае — гомотетия), получим точку x_r и вычислим в ней функцию: f_r = f(x_r). Координаты новой точки вычисляются по формуле:

x_r = (1 + α)x_c − αx_h

4. Далее смотрим, насколько нам удалось уменьшить функцию, ищем место f_r в ряду f_h,f_g,f_l:

4а Если f_r < f_l, то направление выбрано удачное и можно попробовать увеличить шаг — производим растяжение. Новая точка x_e = (1 − γ)x_c + γx_r и значение функции f_e = f(x_e).

• Если f_e < f_l, то можно расширить симплекс до этой точки: заменяем точку x_l на x_e и заканчиваем итерацию (на шаг 8).

Если f_e > f_l, то переместились слишком далеко: в набор берём x_r (опять вместо x_l) и заканчиваем итерацию (на шаг 8).

4b Если f_l < f_r < f_g, то выбор точки уже неплохой (новая лучше двух прежних). Заменяем точку x_h на x_r и переходим на шаг 8.

4с Если f_h > f_r > f_g, то меняем обозначения x_r,x_h (и соответствующие значения функции) местами и идём на шаг 5.

4d Если f_r > f_h, то просто идём на следующий шаг 5.

В результате (возможно, после переобозначения) f_r > f_h > f_g > f_l.

5. Сжатие. Строим точку x_s = βx_h + (1 − β)x_c и вычисляем в ней значение f_s.

6 Если f_s < f_h, то заменяем точку x_h на x_s и идём на шаг 8.

7 Если f_s > f_h, то первоначальные точки оказались самыми маленькими. Делаем глобальное сжатие симплекса — гомотетию к точке с наименьшим значением x_l:

для всех требуемых точек x_i.

8 Последний шаг — проверка сходимости. Может выполняться по-разному, например, оценкой дисперсии набора точек. Суть проверки заключается в том, чтобы проверить взаимную близость полученных вершин симплекса, что предполагает и близость их к искомому минимуму. Если требуемая точность ещё не достигнута, можно продолжить итерации с шага 1.

N-мерный тетраэдр

[править]

Материал из Википедии — свободной энциклопедии

Текущая версия [показать стабильную версию] (сравнить)	(+/-)
Данная версия страницы не проверялась участниками с соответствующими правами. Вы можете прочитать последнюю стабильную версию, проверенную 29 ноября 2009, однако она может значительно отличаться от текущей версии. Проверки требуют 19 правок.

Перейти к: навигация, поиск

Необходимо перенести содержимое этой статьи в статью Симплекс. Вы можете помочь проекту, объединив статьи. Для обсуждения целесообразности перемещения, замените этот шаблон на шаблон {{к объединению}} и добавьте соответствующую запись на странице ВП:КОБ. Пожалуйста, также проверьте историю правок.

N-мерный тетраэдр — простейший возможный в N-мерном пространстве многогранник. Является обобщением для N-мерного пространства таких фигур, как треугольник и трёхмерный тетраэдр.

Содержание [убрать] 1 Построение 2 Описанная сфера 3 Число граней N-тетраэдра 4 Стандартный симплекс 5 Геометрические свойства 6 Формулы для правильного N-тетраэдра 7 Литература 8 См. также 9 Ссылки

[Править] Построение

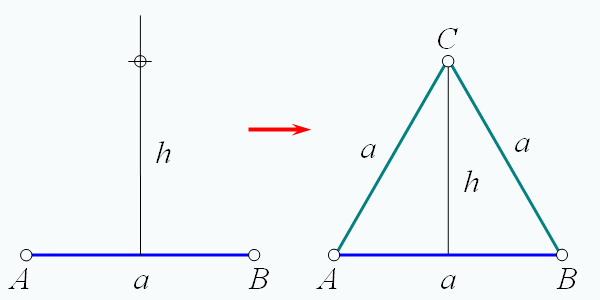
Преобразование 1-тетраэдра в 2-тетраэдр

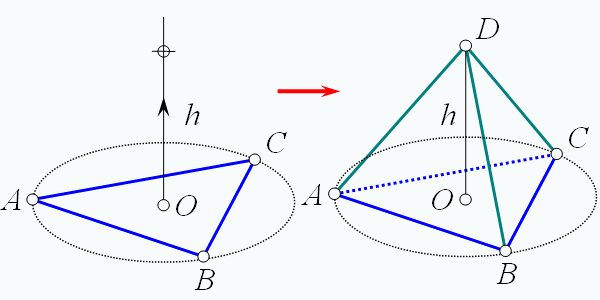
Преобразование 2-тетраэдра в 3-тетраэдр

Как известно, через любые N точек можно провести (N–1)–плоскость и существуют множества из N+1 точек, через которые (N–1)–плоскость провести нельзя. Таким образом, N+1 – минимальное число точек в N–пространстве, которое не лежит в одной (N–1)–плоскости, и может служить вершинами N–многогранника.

Простейший N–многогранник с количеством вершин N+1 называется N–тетраэдром по названию трёхмерного члена этого семейства. В литературе принято также название «симплекс». В пространствах низшей размерности этому определению соответствуют 4 фигуры:

• 0-тетраэдр (точка) – 1 вершина;

• 1–тетраэдр (отрезок) – 2 вершины;

• 2–тетраэдр (треугольник) – 3 вершины;

• 3–тетраэдр (собственно тетраэдр) – 4 вершины.

Все эти фигуры обладают тремя общими свойствами:

1. В соответствии с определением, число вершин у каждой фигуры на единицу больше размерности пространства;

2. Существует общее правило преобразования фигур низшей размерности в фигуры высшей размерности. Оно заключается в том, что из геометрического центра фигуры строится перпендикуляр в следующее измерение, на этом перпендикуляре строится новая вершина и соединяется рёбрами со всеми вершинами исходного тетраэдра;

3. Как следует из описанной в п. 2 процедуры, любая вершина тетраэдра соединена рёбрами со всеми остальными вершинами.

[Править] Описанная сфера

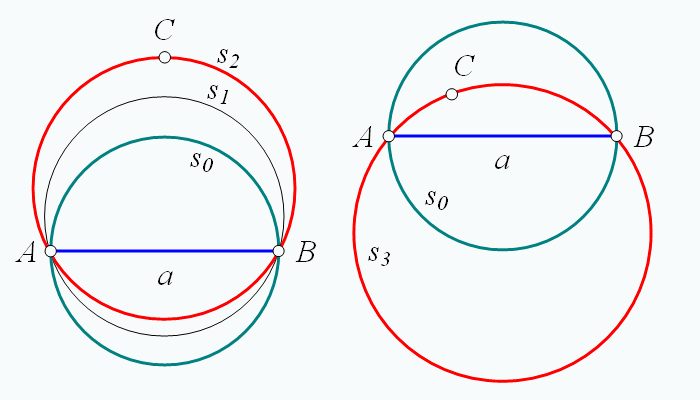
Построение описанной 2-сферы вокруг 1-тетраэдра с дополнительной точкой

Вокруг любого N-тетраэдра можно описать N-сферу.

Для 1-тетраэдра это утверждение очевидно. Описанная 1-сфера будет представлять собой отрезок, совпадающий с самим 1-тетраэдром, и её радиус будет составлять R = a/2. Добавим к 1-тетраэдру ещё одну точку и попробуем описать вокруг них 2-сферу.

Построим 2-сферу s₀ радиусом a/2 таким образом, чтобы отрезок AB был её диаметром. Если точка С находится за пределами окружности s₀, то увеличивая радиус окружности и смещая её в сторону точки С можно добиться того, что все три точки окажутся на окружности. Если же точка С лежит внутри окружности s₀, то подогнать окружность под эту точку можно увеличивая её радиус и смещая в сторону, противоположную точке С. Как видно из рисунка, сделать это можно в любом случае, когда точка С не лежит на одной прямой с точками АВ. Не является помехой и несимметричное расположение точки С относительно АВ.

Рассматривая общий случай, предположим, что существует (N–1)-сфера S_N-1 радиуса r, описанная вокруг некоторой (N–1)-мерной фигуры. Поместим центр сферы в начало координат. Уравнение сферы будет иметь вид

Построим N-сферу с центром в точке (0, 0, 0, ... 0, h_S) и радиусом R, причём

Уравнение этой сферы

или

Подставив в уравнение (1) x_N = 0, получим уравнение (2). Таким образом, при любом h_S сфера S_N-1 является подмножеством сферы S_N, а именно – её сечением плоскостью x_N = 0.

Предположим, что точка С имеет координаты (X₁, X₂, X₃, ..., X_N ). Преобразуем уравнение (2) к виду

и подставим в него координаты точки С:

Выражение в левой части представляет собой квадрат расстояния R_C от начала координат до точки C, что позволяет привести последнее уравнение к виду

откуда можно выразить параметр h_S:

Очевидно, что h_S существует при любых R_C, X_N и r, кроме X_N = 0. Это значит, что если точка С не лежит в плоскости сферы S_N–1, всегда можно найти такой параметр h_S, что на сфере S_N c центром (0, 0, 0, ..., h_S) будет лежать и сфера S_N–1, и точка С. Таким образом, вокруг любых N+1 точек можно описать N–сферу, если N из этих точек лежат на одной (N–1)–сфере, и последняя точка не лежит с ними в одной (N–1)–плоскости.

Применяя последнее по индукции, можно утверждать, что N–сферу можно описать вокруг любых N+1 точек, если они не лежат в одной (N–1)–плоскости.