Практична робота №6

Закони розподілу дискретних та неперервних величин.

Біноміальний розподіл (розподіл Бернулі)

Дискретна випадкова величина Х, яка може приймати тільки цілі невід'ємні значення з ймовірностями , де - ймовірність появи події в кожному випробуванні, m - кількість сприятливих подій, n - загальна кількість випробувань, . називається розподіленою за біноміальним законом з математичним сподіванням , та дисперсією .

Закон Бернулі використовується тоді, коли необхідно знайти ймовірність появи випадкової події яка реалізується рівно раз у серії з випробувань.

Біноміальному закону розподілу підпорядковуються такі випадкові події, як число викликів швидкої допомоги за певний проміжок часу, черги до лікаря в поліклініці, епідемії тощо.

Приклад 1

Нехай X - число рецесивів серед нащадків, отриманих при схрещуванні двох гібридів G1 та G2. За теорією Менделя ймовірність того, що нащадок двох гібридів буде рецесивом дорівнює 0,25. В рамках теорії Менделя X є біноміальною випадковою змінною і ймовірністю:

Тобто, підставляючи певні значення m отримаємо ймовірність рецесивів серед n нащадків.

Розподіл Пуасона

Дискретна випадкова величина X, яка може приймати тільки цілі невід'ємні значення з ймовірностями називається розподіленою за законом Пуассона з математичним сподіванням і дисперсією , де .

Розглядаються малоймовірні події, які відбуваються у довгій серії незалежних випробувань декілька разів.

Розподіл Пуасона, як граничний біноміальний використовується при вирішенні задач надійності медичного обладнання та апаратури, розповсюдження епідемії, викликів до хворого дільничних лікарів та в інших задачах масового обслуговування.

Приклад 2

Вакцина формує імунітет від деякого захворювання з ймовірністю 0,999. Провакциновано 4000 мешканців міста. Яка ймовірність того, що двоє з них не набули імунітету. Знаходимо . Далі знаходимо ймовірність, що двоє з них не набули імунітету :

.

Нормальний закон розподілу (розподіл Гауса)

В біології та медицині найчастіше розглядають випадкові величині, які мають нормальний закон розподілу, наприклад, частота дихання, частота серцевих скорочень, динаміка росту популяції тощо.

Для нормального закону розподілу густина розподілу ймовірності задається рівнянням:

,

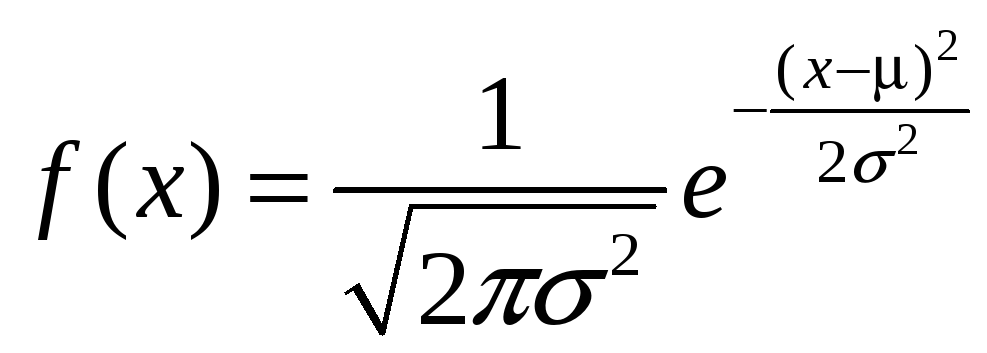де іпараметри розподілу: - математичне сподівання (або середнє значення при n=∞), а - середнє квадратичне відхилення. Дисперсія характеризує квадрат розсіювання випадкової величини.

Стандартним нормальним розподілом називають розподіл з нульовим математичним сподіванням і одиничною дисперсією, густина розподілу якого має наступний вигляд : .

Густина ймовірності стандартного нормального розподілу для трьох різних значень має вигляд, представлений на рис.1.

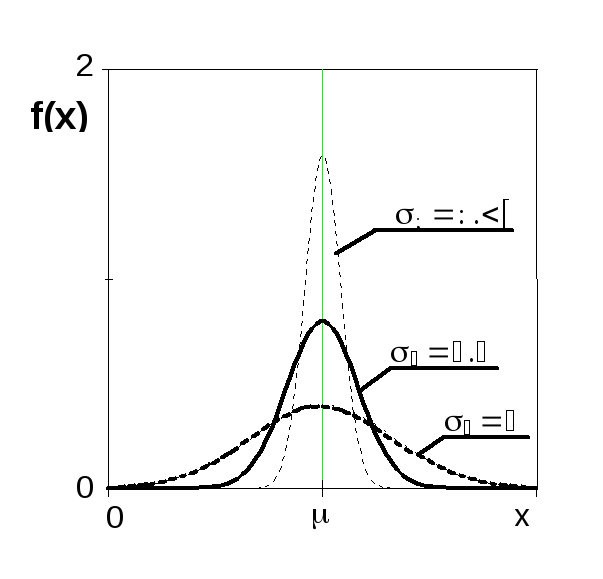
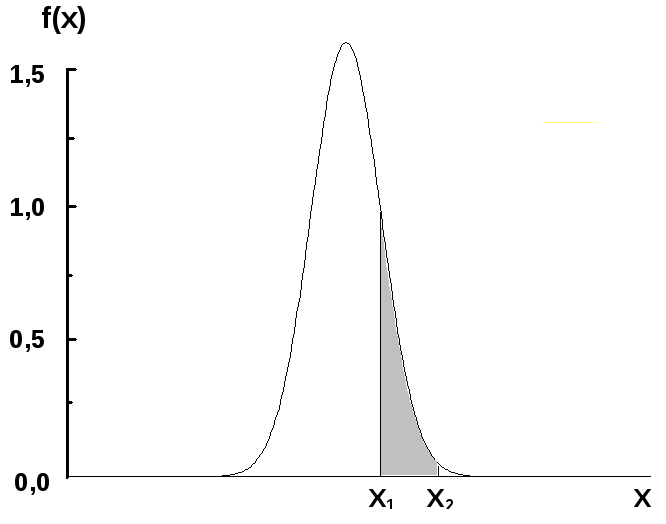
Рис.1. Рис.2

З рис.1 видно, що чим більше значення дисперсії, тобто чим більший ступінь розсіювання випадкових величин, тим більш пологою і розтягнутою стає крива і навпаки. Площа фігури обмежена кривою f (x) і вертикальними прямими, проведеними із точок x₁ и x₂ (рис.2), чисельно рівна ймовірності попадання результату вимірювань в інтервал x = x₁ - x₂, яка називається довірчою ймовірністю а інтервал називається довірчим. Площа під графіком густини розподілу дорівнює 1 – це ймовірність достовірної події. Використовуючи нормальний розподіл, теорія похибок ставить і вирішує дві основні задачі. Перша - оцінка точності проведених вимірів. Друга - оцінка точності середнього арифметичного значення результатів вимірювань.

Основна кількість отриманих результатів групується навколо найбільш ймовірного значення. В практичних застосуваннях важливим правилом є правило «трьох сигм»:

.

Тобто ймовірність того, що нормально розподілена випадкова величина відрізняється від свого математичного сподівання більше, ніж на три сигма, приблизно дорівнює 0,0027. Така подія є практично неможливою.

Розподіл Ст 'юдента (Госсета)

Розглянемо набір результатів вимірювання нормально розподіленої величини х. З цих даних визначимо і . Введемо нову величину , що містить як експериментальне середнє значення так і задане значення вимірюваної величини , яке точно відоме, наприклад із розрахунків та таблиць:

Тоді розподіл величини при кінцевому числі вимірів п буде розподілом Ст'юдента з п ступенями вільності або -розподілом. При збільшенні числа ступенів вільності розподіл Ст'юдента наближається до нормального. Значення коефіцієнтів Ст'юдента для відповідної довірчої ймовірності та кількості ступеней вільності затабульовані.

- розподіл Ст'юдента використовують в математичній статистиці при визначенні оцінок ймовірностей попадання випадкової величини в довірчий інтервал (інтервал, який із заданою ймовірністю р покриває параметр випадкової нормально розподіленої величини):

.

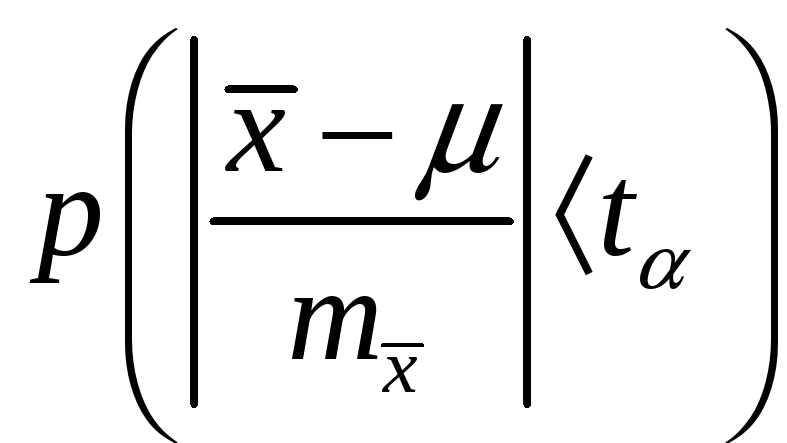Математичне сподівання розподілу Ст'юдента дорівнює 0, а дисперсія - .

Розподіл Фішера

Нехай ми провели дві серії незалежних вимірювань випадкової величини: і з числом вимірювань в серіях і і вибірковими дисперсіями і відповідно. Тоді розподіл випадкової величини називається розподілом Фішера.

Розподіл

Нехай маємо вибірку із п незалежних випадкових величин , розподілених за нормальним законом з =0 та . Якщо для кожної випадкової величини створимо вираз то сума квадратів випадкових величин має закон розподілу, що носить назву - розподіл з ступенями вільності. Із збільшенням ступенів вільності розподіл наближається до нормального розподілу.

Перевірка гіпотези про рівність між середніми значеннями незалежних вибірок здійснюється за допомогою критерію Ст’юдента, або -критерію. Для цього необхідно визначити:

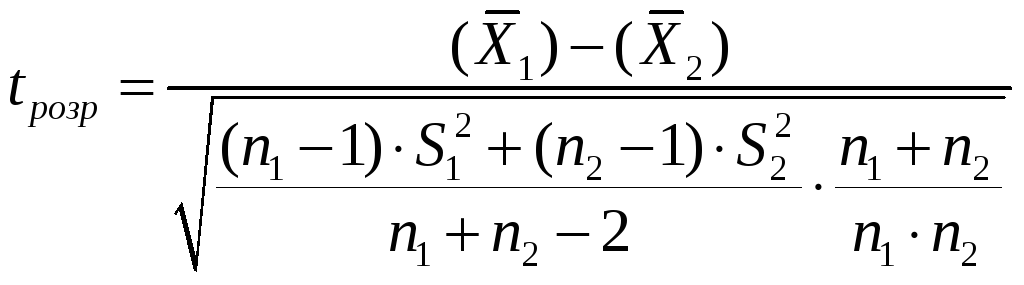(1)

Число ступеней вільності рівне: . Ця формула справедлива для випадку рівності вибіркових дисперсій: .

Для провірки гіпотези про рівність дисперсій використовують критерій Фішера. При цьому визначають як відношення більшої дисперсії до меншої:

; (2)

Обчислене значення порівнюють із табличним з врахуванням числа ступеней вільності ; і довірчої ймовірності. Якщо <, то це означає, що вибірки взяті із сукупностей з рівними дисперсіями. Якщо > то дисперсії відрізняються і необхідно визначати по формулі:

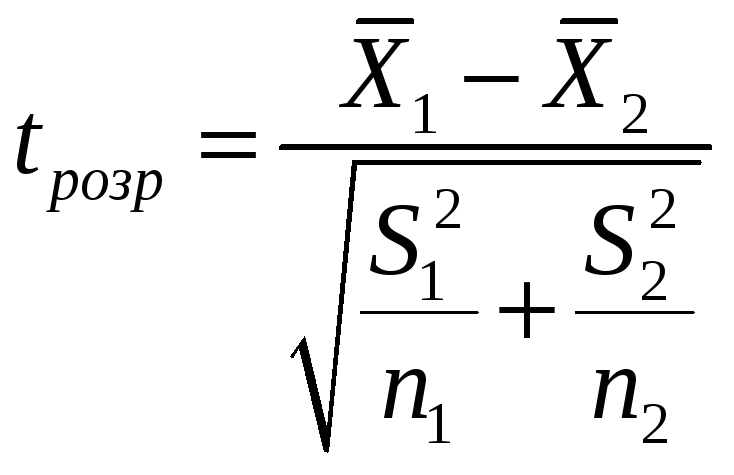(3)

При цьому число ступеней вільності рівне:

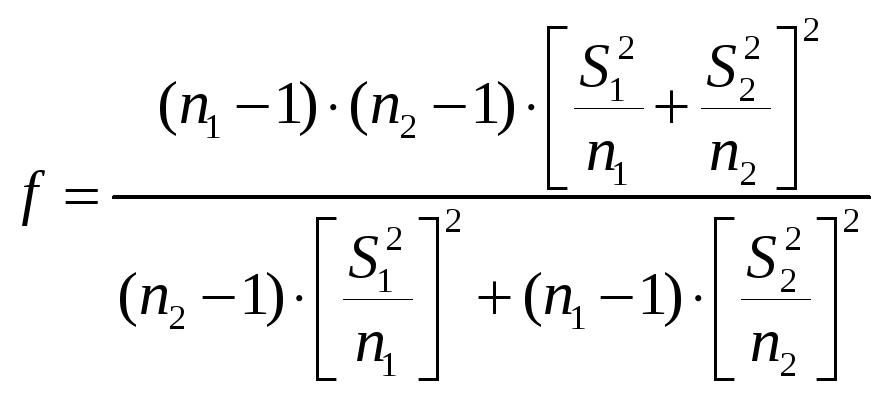(4)

Потім розраховані значення порівнюється з , з врахуванням числа ступеней вільності і довірчої ймовірності . Якщо <, то відмінність між середніми незначуща і вони належать до однєї генеральній сукупності. Якщо >, то відмінність значуща і вибірки відносяться до різних генеральних сукупностей.

Критерій Ст’юдента є параметричним, тобто його можна застосовувати лише до вибірок, що мають нормальний закон розподілу. Тому необхідна перевірка даних на відповідність нормальному закону розподілу.

Перевірка нормальності розподілу за допомогою показників асиметрії і ексцесу

Асиметрія - величина, що характеризує несиметричність розподілу елементів вибірки щодо середнього значення. Приймає значення від - 1 до 1. У разі симетричного розподілу рівна 0. Коефіцієнт асиметрії, або третій центральний момент розподілу, є кількісною характеристикою ступеня скошеності розподілу. Вибірковий коефіцієнт асиметрії визначається по формулі:

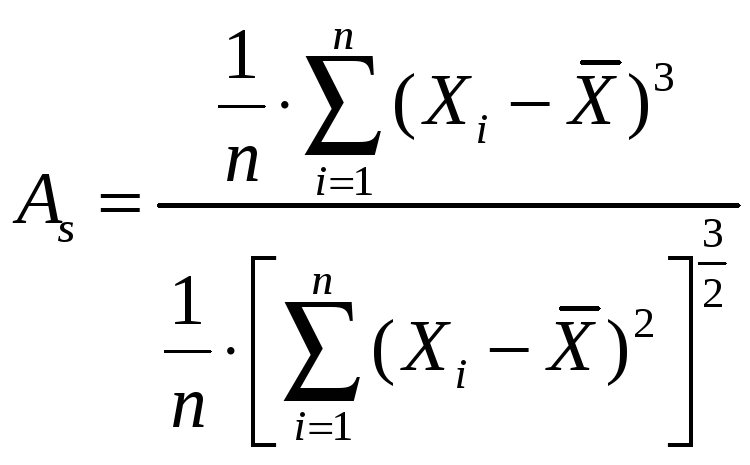
Як випливає із даної формули, коефіцієнт асиметрії є безрозмірною величиною і рівний нулю у симетричних розподілах. Якщо розподіл має довгу частину, розташовану праворуч від вершини, то асиметрію називають позитивною, а розподіл з довгою частиною кривої густини, розташованої зліва від вершини, називають негативною асиметрією.

Ексцес - ступінь вираженості "хвостів" розподілу, тобто частоти появи віддалених від середнього значень. Коефіцієнт ексцесу, або четвертий центральний момент, кількісно характеризує гостровершинність розподілу. Вибірковий коефіцієнт ексцесу обчислюється за формулою:

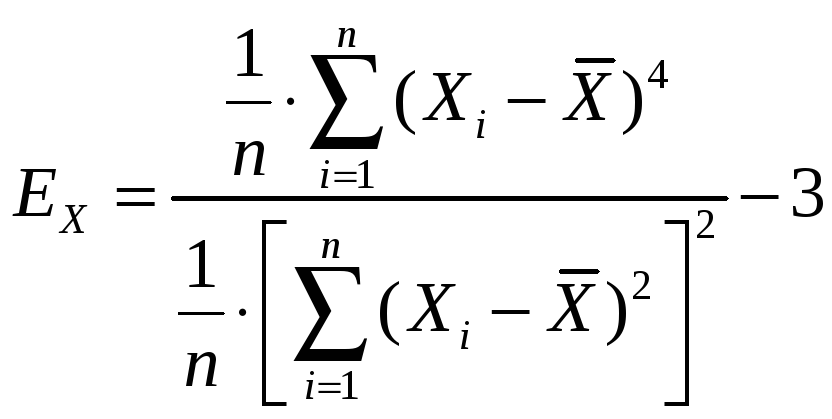
Для нормального (гаусового ) розподілу коефіцієнт ексцесу рівний нулю. Криві розподілу з гострою вершиною мають позитивний ексцес, а з плоскою - негативний. Таким чином, при нормальному законі розподілу вибіркових даних коефіцієнти асиметрії і ексцесу рівні нулю.