лабораторная работа / ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ И КАЧЕСВО ЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМ- / Построение и исследование математических моделей линейных импульсных систем

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ

КАФЕДРА УПРАВЛЕНИЯ И ИНФОРМАТИКИ В ТЕХНИЧЕСКИХ СИСТЕМАХ

ЛАБОРАТОРНАЯ РАБОТА №1

по дисциплине

Теория автоматического управления

Построение и исследование математических моделей

линейных импульсных систем (ЛИС)

Выполнил ст. гр. УИТ-41

Сербаев В.В.

Проверил преподаватель

Мефедова Ю.А.________

«___» ___________2004

2004

Цель работы: исследовать математические модели ЛИС и способы построения этих моделей для линейных непрерывных объектов.

Данные: передаточная функция системы, параметры T=0.2; K=2; d₁=2.5; d₂=1. Передаточная функция примет вид: .

Задание 1. Для заданной передаточной функции W(p) рассчитать W(z), используя матричный метод и метод Z-преобразования. Сравнить полученные результаты.

1. Получение W(z) используя матричный метод

По заданной передаточной функции запишем дифференциальное уравнение: y^//+2.5y^/+y=2u

Перейдем к уравнениям в пространстве состояний:

Следовательно, матрицы:

и

Определим матрицы A и B:

Матрицы С и С совпадают.

Разностные уравнения имеют вид:

По найденному разностному уравнению составлена математическая модель системы, реализованная в Simulink. Структурная схема представлена на рисунке 1.

Рисунок 1

Дискретную передаточную функцию с фиксатором нулевого порядка находим по формуле:

2. Получение W(z) используя z-преобразование

Определим значение

Разобьем выше приведенную форму передаточной функции на элементарные дроби: .

Запишем соответствующие z-преобразования для каждой дроби и умножим их на :

После упрощения получим следующий вид дискретной передаточной функции с фиксатором нулевого порядка:

Как видно полученные разными способами передаточные функции практически идентичны, что подтверждает правильность решения.

2. Воспользуемся пакетом Simulink для определения переходных функций системы.

Рисунок 2 –Модель системы 1

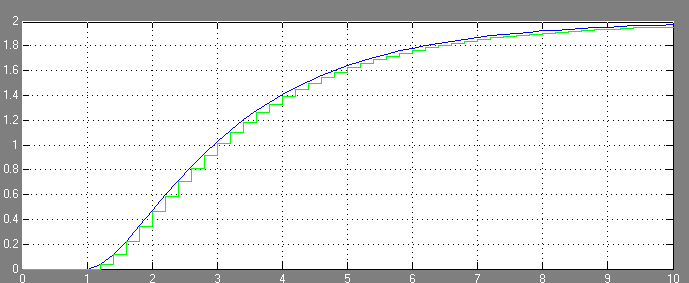
Рисунок 3 – Scope 1

Рисунок 4 - Модели систем 2

Рисунок 3 – Scope 2

Вывод: сравнивая динамические свойства непрерывных и дискретных моделей системы, можно заметить визуальную близость переходных характеристик двух систем. Это наталкивает на мысль о возможности идентичного применения обоих видов систем. Узким местом работы любой дискретной системы становится частота дискретизации. Для заданной системы частота в 0.3 Гц оказалась достаточной для приближения характеристик дискретной и непрерывной системы друг к другу, однако заданная система является достаточно простой. Графики переходных характеристик говорят о достаточно большой зависимости плавности управления от частоты дискретизации. Так дискретная модель полученная пакетом Simulink достаточно далека от модели полученной в ходе лабораторной работы. На Simulink-овской модели наблюдается начальный всплеск уровня сигнала, которого нет на других графиках, т.е. точность управления в системах с ООС оставляет желать лучшего. Как итог, дискретные системы применимы в тех случаях, когда аппаратная поддержка обеспечивает быструю реакцию системы на скоростные изменения входного сигнала.