МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УО «БАРАНОВИЧСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

УТВЕРЖДАЮ

зав. кафедрой физико-математических дисциплин

_____________Ционенко Д.А.

«__» _________ 20__ г, протокол №

Зимняя экзаменационная сессия

Вопросы к зачету по высшей математике

для студентов первого курса специальности «Маркетинг», «Экономика и управление на предприятии», «Бухгалтерский учёт, анализ и аудит в АПК», «Экономика и управление туристской индустрией»

1. Матрицы. Виды матриц.

2. Операции над матрицами.

3. Минор и алгебраическое дополнение элемента матрицы.

4. Определители, их вычисление и свойства.

5. Элементарные преобразования матрицы.

6. Обратная матрица.

7. Системы линейных уравнений. Матричная запись. Матричный метод решения систем линейных уравнений.

8. Решение систем линейных уравнений методом Крамера.

9. Решение систем линейных уравнений методом Гаусса.

10. Векторы. Основные понятия и определения.

11. Скалярное, векторное, смешанное произведение векторов.

12. Базис. Разложении векторов по базису.

13. Прямая на плоскости. Способы задания прямой.

14. Прямая в пространстве. Способы задания прямой.

15. Плоскость. Способы задания плоскости.

16. Окружность. Эллипс. Гипербола. Парабола.

17. Функция. Основные понятия и определения.

18. Графики и свойства элементарных функций.

19. Понятие предела и его свойства.

20. Методы вычисления пределов.

21. Замечательные пределы 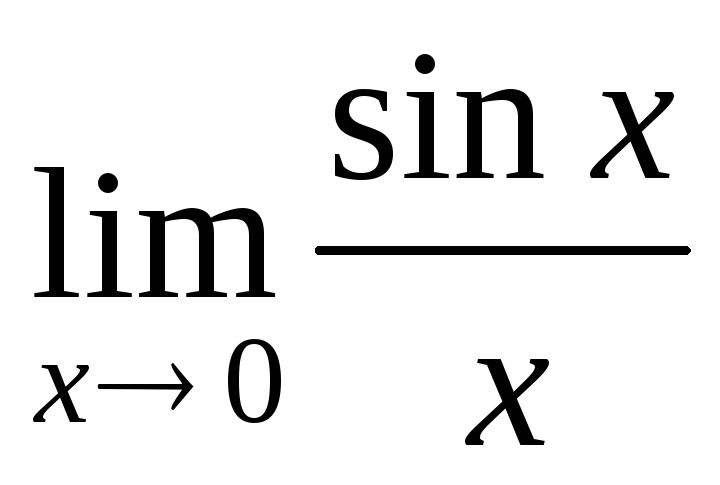и .

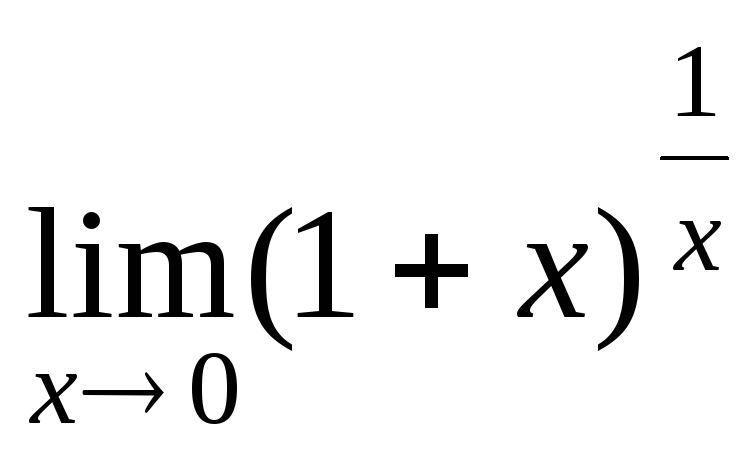22. Производная функции. Правила дифференцирования.

23. Таблица производных элементарных функций.

24. Производная сложной функции. Производная неявной функции и функции, заданной параметрически.

25. Геометрический смысл производной.

26. Правила Лопиталя.

27. Монотонность функции. Критерии монотонности.

28. Критические точкию

29. Экстремумы. Необходимое условие, достаточные условия.

30. Выпуклость. Критерий выпуклости. Перегибы.

31. Нахождение наибольшего и наименьшего значения функции на заданном отрезке.

32. Асимптоты графика функции.

33. Схема исследования функции.

Составил преподаватель кафедры

физико-математических дисциплин Мирошникова Ю.Ф.

Вопросы к экзамену по дисциплине «Высшая математика» для студентов первого курса специальности «Маркетинг», «Экономика и управление на предприятии», «Бухгалтерский учёт, анализ и аудит в АПК», «Экономика и управление туристской индустрией»

1. Понятие n-мерного пространства и типы множеств.

2. Понятие функции нескольких переменных.

3. Частные производные и полный дифференциал первого порядка функции нескольких переменных.

4. Частные производные и полный дифференциал второго порядка функции нескольких переменных.

5. Понятие предела функции нескольких переменных.

6. Экстремум функции нескольких переменных(локальный экстремум).

7. Градиент функции.

8. Условный экстремум.

9. Метод наименьших квадратов.

10. Понятие первообразной и неопределённого интеграла.

11. Неопределенный интеграл и его свойства.

12. Таблица неопределённых интегралов.

13. Основные методы интегрирования(метод замены переменной, интегрирование по частям, непосредственное интегрирование).

14. Интегрирование выражений, содержащих квадратный трёхчлен .

15. Интегрирование тригонометрических и иррациональных функций.

16. Интегрирование рациональных функций.

17. Алгоритм разложения правильной дроби на элементарные.

18. Задача о криволинейной трапеции.

19. Определенный интеграл и его свойства.

20. Основные методы интегрирования определённых интегралов.

21. Приложения определенного интеграла: площадь плоской фигуры.

22. Приложения определенного интеграла: объем тела вращения.

23. Приложения определенного интеграла: длина дуги.

24. Несобственные интегралы.

25. Кратные интегралы.

26. Обыкновенные дифференциальные уравнения: основные понятия и определения.

27. Дифференциальные уравнения с разделяющимися переменными.

28. Однородные дифференциальные уравнения первого порядка.

29. Линейные дифференциальные уравнения первого порядка.

30. Понятие комплексного числа.

31. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

32. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

33. Числовые ряды: основные понятия и определения.

34. Гармонический ряд.

35. Ряды с положительными членами.

36. Необходимый признак сходимости числового ряда .

37. Сравнительные признаки сходимости числовых рядов.

38. Признаки сходимости числовых рядов: признак Даламбера, признак Коши.

39. Знакочередующиеся ряды. Абсолютная и условная сходимость.

40. Степенные ряды. Радиус и интервал сходимости степенного ряда.

41. Ряд Тейлора.

42. Ряд Маклорена. Разложения функций в ряд Маклорена.

Линии второго порядка на плоскости.

Линии, уравнения которых в прямоугольной систем координат являются уравнениями второй степени, называются линиями второго порядка. К важнейшим линиям второго порядка относятся эллипс, окружность, гипербола и парабола.

8.1. Эллипс. Окружность.

Определение 4.1. Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.

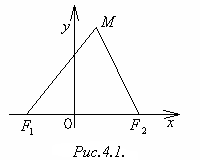Пусть F₁(-c,0) и F₂(c,0) ─ фокусы. Тогда F₁F₂ = 2c ─ фокусное расстояние (рис.4.1). Постоянную величину, о которой идёт речь в определении эллипса, обозначим 2a.

Пусть M(x,y) ─ произвольная точка эллипса. Тогда по определению F₁M + F₂M = 2a > 2c, откуда a > c.

Так как F₁M = , F₂M = , то имеем уравнение + = 2a.

Преобразуем это уравнение:

()² = (2a − )² ,

(x² + 2cx + c²) + y² = 4a² – 4a+ (x² –­ 2cx + c²) + y²,

a = a² – cx.

Возводя в квадрат последнее уравнение, имеем

a²(x² – 2cx + c² + y²) = a⁴ – 2cxa² + c²x²,

(a² – c²)x² + a²y² = a²(a² – c²).

Так как a > c, то a² – c² > 0 и можем обозначить b² = a² – c². Тогда

b²x² + a²y² = a²b²,

= 1 (1)

Таким образом, координаты любой точки эллипса удовлетворяют уравнению (1).

Покажем обратное: если координаты точки M(x,y) удовлетворяют уравнению (1), то точка M лежит на эллипсе.

Из (1) найдём y² : y² = b²(1 - ).

Тогда F₁M = = = == = = ││

Т.к. c < a и из (1) ≤ 1, т.е. x² ≤ a² , │x│ ≤ a, то . Следовательно,

││= .

Аналогично можно вычислить

F₂M = .

Теперь

F₁M + F₂M = .

Из уравнения (1) : b² > 0  a² – c² > 0, т.е. a > c, откуда 2a > 2c. Значит, точка M лежит на эллипсе.

Уравнение (1) называется каноническим уравнением эллипса. Изображён эллипс с уравнением (1) на рис 4.2.

Т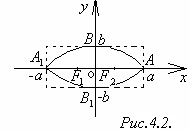очки пересечения эллипса с осями координат называются вершинами эллипса. Оси симметрии эллипса (оси Ox и Oy) называют осями эллипса. Точка пересечения осей ─ центр эллипса. Осями называют также отрезки A₁A, B₁B. Отрезки OA, OB и их длины называют полуосями. В нашем случае a > b, поэтому а называют большой полуосью, b ─ малой полуосью. Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большой оси, т.е.

ε = .

Так как 0 c < a, то 0 ε < 1. Фокальными радиусами точки M называют отрезки F₁M и F₂M. Их длины r₁ и r₂ вычисляют по формулам

r₁ = a + εx,

r₂ = a – εx.

Уравнение (1) можно рассматривать и в случае, когда b > a, оно определяет эллипс с большой полуосью OB = b, фокусы такого эллипса лежат на оси Oy, причём a² = b² – c².

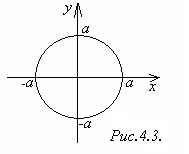
В случае, когда a = b, уравнение (1) принимает вид

= 1 или x² + y² = a²

и определяет окружность радиуса а с центром в начале координат (рис.4.3). В этом случае c = 0, поэтому ε = 0.

Из школьного курса известно уравнение окружности радиуса R с центром в точке A₀(x₀,y₀):

(x – x)+(y – y)=R.

Такое уравнение называют каноническим уравнением окружности.