
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Саратовский государственный технический университет Определение коэффициента поверхностного натяжения жидкости методом капель
Методические указания
к выполнению лабораторной работы по физике
для студентов всех специальностей
Электронное издание локального распространения
Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета
Саратов—2006
Все права на размножение и распространение в любой форме остаются за разработчиком.
Нелегальное копирование и использование данного продукта запрещено.
Составитель - Евсеева Лидия Алексеевна.
Под редакцией - Зюрюкина Юрия Анатольевича.
Рецензент - Вахлюева Валентина Ивановна
410054, Саратов, ул. Политехническая 77,
Научно-техническая библиотека СГТУ,
тел. 52-63-81, 52-56-01
http: // lib.sstu.ru
Регистрационный
номер 060543Э
© Саратовский государственный
технический университет 2006 г.
Ц е л ь р а б о т ы: определение коэффициента поверхностного натяжения жидкости методом капель.
Теоретические представления о поверхностном натяжении
Поверхностное натяжение является одной из основных характеристик жидкого состояния вещества. Оно проявляется в особом поведении поверхностного слоя жидкости, который стремится сократиться. Это связано с различным характером взаимодействия молекул внутри жидкости и на её поверхности.
Каждая
молекула жидкости взаимодействует с
другими молекулами, окружающими её.
Силы взаимодействия специфичны, т. е.
существенно зависят от природы
взаимодействующих молекул и сильно
различаются по величине для разных
жидкостей. Между молекулами жидкости
одновременно существуют как силы
притяжения, так и силы отталкивания.
Эти силы различны по своей природе, чем
и обусловлен различный характер их
зависимости от расстояния между
взаимодействующими молекулами. На очень
малых расстояниях преобладают силы
отталкивания, на более далеких расстояниях
— силы притяжения. Межмолекулярные
силы очень быстро убывают с расстоянием.
Поэтому, начиная с некоторого расстояния
![]() ,
силами притяжения между молекулами
можно пренебречь. Это расстояние
называется радиусом молекулярного
действия, а сфера радиуса
,
силами притяжения между молекулами
можно пренебречь. Это расстояние
называется радиусом молекулярного
действия, а сфера радиуса
![]() называется сферой молекулярного
действия. Радиус молекулярного действия
имеет величину порядка размеров
молекулы(
называется сферой молекулярного
действия. Радиус молекулярного действия
имеет величину порядка размеров
молекулы(![]() ~10-9
м).
~10-9
м).
К аждая
молекула испытывает притяжение со
стороны всех соседних с ней молекул,
находящихся в пределах сферы молекулярного
действия, центр которой совпадает с
данной молекулой (рис. 1). Если молекула
находится внутри жидкости, то она
окружена со всех сторон другими
молекулами. Поэтому суммарная сила,
действующая на молекулу, равна нулю.
Если молекула находится на расстоянии
от поверхности, меньшем, чем
аждая
молекула испытывает притяжение со
стороны всех соседних с ней молекул,
находящихся в пределах сферы молекулярного
действия, центр которой совпадает с
данной молекулой (рис. 1). Если молекула
находится внутри жидкости, то она
окружена со всех сторон другими
молекулами. Поэтому суммарная сила,
действующая на молекулу, равна нулю.
Если молекула находится на расстоянии
от поверхности, меньшем, чем
![]() ,
то результирующая сила
,
то результирующая сила
![]() ,
равная сумме всех сил, действующих на
молекулу со стороны соседних молекул,
оказавшихся в сфере молекулярного
действия, отлична от нуля и направлена
внутрь жидкости перпендикулярно её
поверхности (рис. I) .
,
равная сумме всех сил, действующих на
молекулу со стороны соседних молекул,
оказавшихся в сфере молекулярного
действия, отлична от нуля и направлена
внутрь жидкости перпендикулярно её
поверхности (рис. I) .
Это объясняется тем, что концентрация (т.е. число, молекул находящихся в единице объема) жидкости больше концентрации пара этой жидкости или воздуха, расположенных над поверхностью жидкости, в результате чего каждая молекула на поверхности окружена со стороны жидкости большим числом близлежащих соседей, чем со стороны пара (воздуха). Следовательно, к каждой молекуле, находящейся на поверхности жидкости, приложены силы, стремящиеся переместить её внутрь жидкости. Поэтому поверхность жидкости стремится сократиться. Стремление жидкости сократить свою свободную поверхность называется поверхностным натяжением.
Если бы форма жидкости определялась только силами межмолекулярного взаимодействия, то жидкость приняла бы такую форму, при которой в поверхностном слое было минимальное при данном объеме число молекул, то есть форму шара (так это и происходит в условиях невесомости). Поэтому форма свободно падающих капель жидкости близка к шарообразной.
Переход молекул из глубины жидкости в поверхностный слой связан с необходимостью совершения работы против действующих в поверхностном слое сил. Эта работа совершается молекулой за счет запаса её энергии и идёт на увеличение потенциальной энергии молекулы. Следовательно, молекулы в поверхностном слое имеют избыточную потенциальную энергию по сравнению с молекулами внутри жидкости. Эта избыточная потенциальная энергия называется свободной поверхностной энергией. Из-за наличия свободной поверхностной энергии жидкость обнаруживает стремление к сокращению своей поверхности.
Выделим мысленно часть поверхности жидкости, ограниченную замкнутым конкуром длиной L. Тенденция этого участка к сокращению приводит к тому, что он действует на граничащие с ним участки с силами, распределенными по всему контуру. Эти силы называются силами поверхностного натяжения. Направлена сила поверхностного натяжения по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует.
Для
количественной характеристики силы
поверхностного натяжения жидкости
вводят коэффициент поверхностного
натяжения σ, который численно равен
силе F,
действующей на единицу длины произвольного
контура L,
мысленно проведенного на поверхности
жидкости: σ=![]() .В
этом случае коэффициент поверхностного
натяжения измеряется в Н/м.
.В
этом случае коэффициент поверхностного
натяжения измеряется в Н/м.
Можно определить коэффициент поверхностного натяжения σ иначе, пользуясь понятием свободной поверхностной энергии.
Величина
свободной поверхностной энергии W
пропорциональна числу молекул, находящихся
на поверхности, т.е. в конечном счете,
пропорциональна площади поверхности
W=σS.
Коэффициент пропорциональности σ=![]() называется свободной удельной энергией
и численно равен свободной энергии
единицы поверхности слоя жидкости.
Свободная удельная энергия σ измеряется
в Дж/м
называется свободной удельной энергией
и численно равен свободной энергии
единицы поверхности слоя жидкости.
Свободная удельная энергия σ измеряется
в Дж/м![]() .
Удельная свободная энергия σ и коэффициент
поверхностного натяжения σ равны.
.
Удельная свободная энергия σ и коэффициент
поверхностного натяжения σ равны.
Коэффициент поверхностного натяжения различен для разных жидкостей, он зависит от рода жидкости, температуры (для большинства жидкостей поверхностное натяжение падает с ростом температуры практически по линейному закону) и от степени чистоты поверхности (изменяется от малейшего загрязнения). На величину коэффициента поверхностного натяжения существенно влияют растворенные в жидкости примеси. Если энергия взаимодействия молекулы растворенного вещества с молекулами растворителя меньше энергии взаимодействия молекул растворителя между собой, то растворенные молекулы будут вытесняться (адсорбироваться) на поверхности жидкости и уменьшать свободную поверхностную энергию, т.е. поверхностное натяжение. Вещества, снижающие поверхностное натяжение, называются поверхностно-активными веществами по отношению к данной жидкости. Простейшими поверхностно-активными веществами по отношению к воде являются спирты, жирные кислоты и их соли (мыла).
Е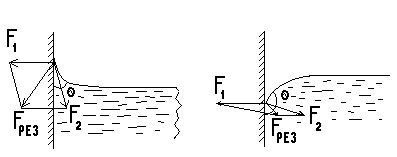 сли
жидкость находится в сосуде, то кроме
свободной поверхности существует еще
одна граница раздела между жидкостью
и твердым телом – стенками сосуда. У
поверхности твердого тела молекулы
жидкости взаимодействуют не только
между собой, но и с молекулами твердого
тела. Если сила взаимодействия между
молекулами жидкости и твердого тела
сли
жидкость находится в сосуде, то кроме
свободной поверхности существует еще
одна граница раздела между жидкостью
и твердым телом – стенками сосуда. У
поверхности твердого тела молекулы
жидкости взаимодействуют не только
между собой, но и с молекулами твердого
тела. Если сила взаимодействия между
молекулами жидкости и твердого тела
![]()
![]() (рис.2а) больше силы взаимодействия
между молекулами жидкости
(рис.2а) больше силы взаимодействия
между молекулами жидкости
![]()
![]() ,
то равнодействующая сила
,
то равнодействующая сила
![]() рез=
рез=
![]()
![]() +
+![]()
![]() направлена
в сторону твердого тела. В этом случае
жидкость смачивает твердое тело.
направлена
в сторону твердого тела. В этом случае
жидкость смачивает твердое тело.
а рис.2 б
При
F![]() >
F
>
F![]() результирующая
сила направлена внутрь жидкости, в этом
случае жидкость не смачивает твердое
тело. Одно и то же твердое тело может
смачиваться водой, но не смачиваться
ртутью.
результирующая
сила направлена внутрь жидкости, в этом
случае жидкость не смачивает твердое
тело. Одно и то же твердое тело может
смачиваться водой, но не смачиваться
ртутью.
В
равновесном состоянии поверхность
жидкости у твердой стенки перпендикулярна
к равнодействующей силе
![]() рез.
Эта поверхность называется мениском.
Явление смачивания характеризуется
краевым углом θ
между поверхностью твердого тела и
мениском в точках их пересечения (рис.
2б).
рез.
Эта поверхность называется мениском.
Явление смачивания характеризуется
краевым углом θ
между поверхностью твердого тела и
мениском в точках их пересечения (рис.
2б).
Для
жидкости, смачивающей данную поверхность,
краевой угол острый (θ<![]() ),
а мениск - вогнутый (рис.2а). Краевой угол
для несмачивающих жидкостей тупой (
),
а мениск - вогнутый (рис.2а). Краевой угол
для несмачивающих жидкостей тупой (![]() <
θ< π), а
мениск выпуклый (рис.2б).
<
θ< π), а
мениск выпуклый (рис.2б).
Искривление
поверхностного слоя приводит к появлению
дополнительного давления на жидкость
ΔP,
зависящего от поверхностного натяжения
σ и кривизны поверхности H=![]() (
(![]() +
+![]() ),
где R1
и R2
- радиусы кривизны двух взаимоперпендикулярных
сечений поверхности (если поверхность
сферическая, то R1=R2).
ΔP=2
σH.
),
где R1
и R2
- радиусы кривизны двух взаимоперпендикулярных
сечений поверхности (если поверхность
сферическая, то R1=R2).
ΔP=2
σH.
Добавочное давление ΔP направлено к центру кривизны поверхности ΔP>0, если мениск выпуклый и ΔP<0, если мениск вогнутый.
По закону Лапласа давление под искривленной поверхностью жидкости равно P=P0+ΔP=P0+2σH, где P0 - давление при плоской поверхности жидкости.
В узких трубках (капиллярах) вследствие смачивания или несмачивания жидкостью стенок капилляра кривизна поверхности становится значительной. Возникающее при этом дополнительное давление ΔP вызывает заметное о пускание (рис.3а) или
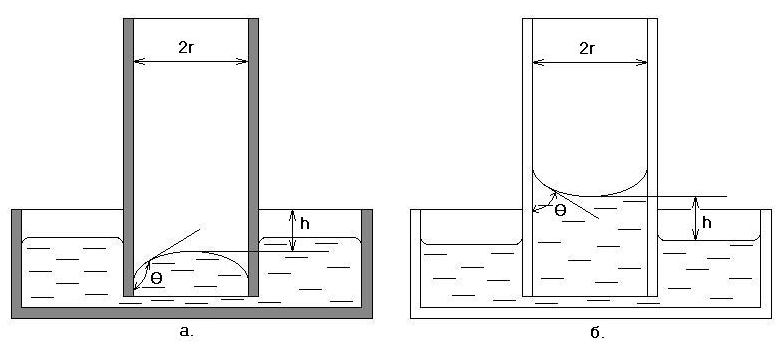
рис 3
поднятие
(рис. 3б) уровня жидкости на величину h:
h=![]() .
В этой формуле σ - коэффициент поверхностного
натяжения, θ
- краевой угол, r
- радиус капилляра, ρ-
плотность жидкости , g-
ускорение свободного падениия.
.
В этой формуле σ - коэффициент поверхностного
натяжения, θ
- краевой угол, r
- радиус капилляра, ρ-
плотность жидкости , g-
ускорение свободного падениия.
Методика эксперимента
К оэффициент
поверхностного натяжения жидкости
определяется методом капель. Исследуемая
жидкость налита в стеклянную трубку,
заканчивающуюся капилляром малого
радиуса r,
из которого вытекает жидкость в виде
капель (рис.4)Рассмотрим процесс
образования капель. Вытеканию жидкости
из капилляра препятствует поверхностная
пленка, состоящая из молекул жидкости.
Под воздействием силы тяжести пленка
прогибается, растягивается, увеличивается,
стремясь приобрести сферическую форму.
В некоторый момент у капли появляется
перетяжка («шейка»), радиус которой
можно приблизительно считать равным
радиусу капилляра. По окружности этой
перетяжки действуют силы поверхностного
натяжения, препятствующие отрыву капли.
Силу поверхностного натяжения F
при отрыве капли можно подсчитать, зная
радиус шейки r:
оэффициент
поверхностного натяжения жидкости
определяется методом капель. Исследуемая
жидкость налита в стеклянную трубку,
заканчивающуюся капилляром малого
радиуса r,
из которого вытекает жидкость в виде
капель (рис.4)Рассмотрим процесс
образования капель. Вытеканию жидкости
из капилляра препятствует поверхностная
пленка, состоящая из молекул жидкости.
Под воздействием силы тяжести пленка
прогибается, растягивается, увеличивается,
стремясь приобрести сферическую форму.
В некоторый момент у капли появляется
перетяжка («шейка»), радиус которой
можно приблизительно считать равным
радиусу капилляра. По окружности этой
перетяжки действуют силы поверхностного
натяжения, препятствующие отрыву капли.
Силу поверхностного натяжения F
при отрыве капли можно подсчитать, зная
радиус шейки r:
F=2πrσ (1)
где σ- коэффициент поверхностного натяжения
рис 4 жидкости.
В момент отрыва капли ее вес P равен силе поверхностного натяжения F, т.е.
P=2πrσ (2)
Если известны P и r, то можно определить σ. Однако измерить радиус шейки r очень сложно, поэтому на практике часто пользуются методом сравнения коэффициентов поверхностного натяжения двух жидкостей – исследуемой и эталонной, коэффициент поверхностного натяжения которой уже известен. В качестве эталонной жидкости обычно используют дистиллированную воду. В момент отрыва капли воды
P0=2πrσ0 (3)
где P0 - вес капли воды;
σ0 - коэффициент поверхностного натяжения при данной температуре.
Поделив
почленно равенство (2) на равенство (3),
получим
![]() ,
откуда σ=σ0*
,
откуда σ=σ0*![]() (4)
(4)
Учтем, что
P=mg=ρVкg=ρ*![]() *g
(5)
*g
(5)
и
P0=m0g=ρ0V0g=ρ0*
![]() *g
(6),
*g
(6),
где m и Vк – масса и объем одной капли исследуемой жидкости,
m0 и V0 - масса и объем одной капли воды;
ρ - плотность исследуемой жидкости;
ρ0 - плотность воды;
N - количество капель исследуемой жидкости, содержащихся в объеме V.
N0 – количество капель воды, содержащихся в том же объеме.
Подставляя значения Р и Р0 из формул (5) и (6) в формулу (4), получим
σ=σ0![]() (7)
(7)
Полученная
формула является рабочей формулой для
определения коэффициента поверхностного
натяжения исследуемой жидкости. По
формуле (7) коэффициент поверхностного
натяжения исследуемой жидкости
определяется через различные физические
величины σ,ρ,ρ0,
количество капель N0,N.
Все величины вносят определенный вклад
в погрешность поверхностного натяжения
исследуемой жидкости σ. Значение σ0
определяется по таблице 2 с учетом
температуры в лаборатории с точностью
до 0,5*10![]()
![]() .
Абсолютная погрешность Δσ0
=0.5* 10
.
Абсолютная погрешность Δσ0
=0.5* 10![]()
![]() является систематической. Значения
плотностей дистиллированной воды ρ0
и исследуемой жидкости Δρ
взяты табличными:
является систематической. Значения
плотностей дистиллированной воды ρ0
и исследуемой жидкости Δρ
взяты табличными:
ρ0=(0.998![]() 0.0005)
*10
0.0005)
*10![]() кг*м
кг*м![]() ,
ρ=(0,80
,
ρ=(0,80![]() 0,005)*
10
0,005)*
10![]() кг*м
кг*м![]()
Абсолютные
погрешности Δρ0=0.0005*10![]() кг*м
кг*м![]() и
Δρ=0,005*10
и
Δρ=0,005*10![]() кг*м
кг*м![]() являются систематическими. Погрешность
в определении количества капель
дистиллированной воды ΔN0
и количества капель исследуемой жидкости
ΔN
являются случайными. Порядок нахождения
погрешностей ΔN0
и ΔN
описаны в разделе «Производство опыта».
Формула для подсчета коэффициента
поверхностного натяжения исследуемой
жидкости с учетом вкладов всех погрешностей
Δσ0,Δρ0,Δρ,ΔN0,ΔN
приведена в разделе «Обработка результатов
эксперимента».
являются систематическими. Погрешность
в определении количества капель
дистиллированной воды ΔN0
и количества капель исследуемой жидкости
ΔN
являются случайными. Порядок нахождения
погрешностей ΔN0
и ΔN
описаны в разделе «Производство опыта».
Формула для подсчета коэффициента
поверхностного натяжения исследуемой
жидкости с учетом вкладов всех погрешностей
Δσ0,Δρ0,Δρ,ΔN0,ΔN
приведена в разделе «Обработка результатов
эксперимента».
