
- •Уравнение теплового баланса
- •Определение потерь теплоты через ограждающие поверхности.
- •2.1.Выделение однотипных элементов теплоизолирующих ограждений.
- •2.2.Теплопотери через плоскую стенку.
- •2.3.Теплопотери через стенки цилиндра
- •2.4.Теплопотери через стенки сферической поверхности.
- •2.5.Суммарные теплопотери через ограждающие поверхности.
- •4.Расчёт теплообменника.
- •4.1. Определение тепловой мощности теплообменника.
- •4.2. Определение параметров теплообменника.
4.Расчёт теплообменника.
4.1. Определение тепловой мощности теплообменника.
Учитывая тепловой излучатель с тепловым балансом (1.1) теплота, получаемая в теплообменнике, передаётся тепловому излучателю, но часть её теряется при транспортировке по теплотрассе. Так как теплота пропорциональна соответствующему тепловому потоку, то тепловой баланс можно представить следующим образом:
 (4.1)
(4.1)
где
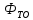 – тепловой поток от теплообменника в
теплотрассу, Вт;
– тепловой поток от теплообменника в
теплотрассу, Вт;
 – тепловой поток
потерь по теплотрассе от теплообменника
до теплового излучателя, Вт;
– тепловой поток
потерь по теплотрассе от теплообменника
до теплового излучателя, Вт;
 – поток с поверхности
излучателя, Вт.
– поток с поверхности
излучателя, Вт.
В момент прохождения (течения) теплоносителя по теплотрассе, путём теплообмена, теплота передаётся внутреннему слою. Затем поток теплоты проходит второй (внешний) слой путём теплопроводности, после чего теплота излучается в окружающую среду за счёт лучистого теплообмена. Поскольку внутренний слой теплотрассы тонкий, а его теплопроводность достаточно высокая, можно принять допущение, сто весь внутренний слой теплотрассы имеет одинаковую температуру, равную температуре теплоносителя. Основываясь на принципе непрерывности теплового потока, можно записать систему уравнений:
 =
=
 (4.2)
(4.2)
 =
=
 σ
σ (4.3)
(4.3)
где
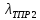 – теплопроводность второго (наружного)
слоя теплотрассы,
– теплопроводность второго (наружного)
слоя теплотрассы,
 ;
;
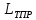 – длинна теплотрассы,
м;
– длинна теплотрассы,
м;
 – температура
теплоносителя, К;
– температура
теплоносителя, К;
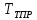 – температура на
поверхности теплотрассы, К;
– температура на
поверхности теплотрассы, К;
 ,
,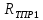 – внешний и внутренний радиусы второго
слоя теплотрассы, м;
– внешний и внутренний радиусы второго
слоя теплотрассы, м;
 - коэффициент
черноты поверхности теплотрассы;
- коэффициент
черноты поверхности теплотрассы;
 - площадь поверхности
теплотрассы,
- площадь поверхности
теплотрассы,
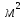 .
.
Приравняв уравнения (4.2) и (4.3), получаем следующее:
 +
+

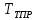 -
-

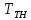 = 0 (4.4)
= 0 (4.4)
Здесь
А =
 ;
;
В =
 ;
;
С =
 σ
σ .
.
Поскольку необходимо
найти внешний и внутренний радиусы
второго слоя теплотрассы (
 ,
, ). Они будут находиться по следующим
формулам:
). Они будут находиться по следующим
формулам:
 =
=
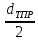 +
+
 =
=
 + 0,03 = 0,0675 м; (4.5)
+ 0,03 = 0,0675 м; (4.5)
 =
=
 +
+
 = 0,0675 + 0,15 = 0,2175 м. (4.6)
= 0,0675 + 0,15 = 0,2175 м. (4.6)
где
 – диаметр внутренний, м;
– диаметр внутренний, м;
 ,
, – толщина внутреннего и внешнего слоя
теплопровода, м.
– толщина внутреннего и внешнего слоя
теплопровода, м.
Уравнение (4.4) можно
решить относительно
 ,
применив функцию пакета стандартных
программ Microsoft
Excel
«Подбор параметра» или «Поиск решения».
При введённых данных получается
,
применив функцию пакета стандартных
программ Microsoft
Excel
«Подбор параметра» или «Поиск решения».
При введённых данных получается
 = 236,4 К.
= 236,4 К.
Найденная температура
поверхности теплотрассы ( ),
подставляется в формулу (4.2) и выходит,
что тепловой поток с поверхности
теплотрассы от теплообменника до
теплового излучателя будет равен:
),
подставляется в формулу (4.2) и выходит,
что тепловой поток с поверхности
теплотрассы от теплообменника до
теплового излучателя будет равен:
 0,05∙5,67∙
0,05∙5,67∙ ∙27,318∙
∙27,318∙ 430,2
Вт.
430,2
Вт.
Следовательно, мощность теплообменника должна быть следующая:
 430,2
+ 10515,5 = 10945,7 Вт.
430,2
+ 10515,5 = 10945,7 Вт.
4.2. Определение параметров теплообменника.
Теплообменник обладает следующими параметрами: число рядов, число труб в ряду, размер труб, мощность теплового потока первичного теплоносителя.
Для того, чтобы определить число труб, необходимо наитии их площадь, а площадь их вычисляется по следующей формуле:

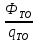 (4.7)
(4.7)
Удельный поток теплоты от первичного теплоносителя к трубам теплообменника определяется по закону Ньютона:
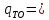 α(
α(
 )
(4.8)
)
(4.8)
где
α
– средний коэффициент теплоотдачи,
 ;
;
 – средняя температура
первичного теплоносителя, К;
– средняя температура
первичного теплоносителя, К;
 – температура на
поверхности труб теплообменника, К.
– температура на
поверхности труб теплообменника, К.
Среднюю температуру первичного теплоносителя можно определить по формуле:

 =
=
 =950 К.
(4.9)
=950 К.
(4.9)
где
 - температура первичного теплоносителя
на входе и выходе теплообменника
соответственно, К.
- температура первичного теплоносителя
на входе и выходе теплообменника
соответственно, К.
Температура на поверхности труб теплообменника приблизительно равна температуре вторичного теплоносителя на выходе, так как трубы имеют малую толщину и высокий коэффициент теплопередачи. Температуру теплоносителя на выходе из теплообменника можно определить из уравнения:

 (4.10)
(4.10)
где
 - потери теплоты по теплотрассе, К.
- потери теплоты по теплотрассе, К.
Так как тепловой поток пропорционален температуре, то потери температуры по теплотрассе можно определить из соотношения:
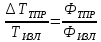 (4.11)
(4.11)
В ходе выведения
потерь теплоты ( )
из выше упомянутого соотношения (4.11),
получается:
)
из выше упомянутого соотношения (4.11),
получается:


 = 353∙
= 353∙
 = 14 К
(4.12)
= 14 К
(4.12)
Подставив полученные данные в формулу (4.10) температура на поверхности труб теплообменника получается:
 353
+ 14 = 367 К.
353
+ 14 = 367 К.
Далее необходимо найти коэффициент теплоотдачи, который зависит от режима течения первичного теплоносителя. В соответствии с теорией подобия, необходимый режим течения определяется критерием Рейнольдса.
Re
=
 (4.13)
(4.13)
где ω
– скорость течения первичного
теплоносителя в самом узком месте
теплообменника,
 ;
;
 – внешний диаметр
труб теплообменника, м;
– внешний диаметр
труб теплообменника, м;
ν – вязкость
первичного теплоносителя,
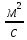 ;
;
Вязкость первичного
теплоносителя берётся в зависимости
от температуры. При температуре воздуха
950К вязкость воздуха равна 118,95∙
 . Применив
соответствующие данные, критерий
Рейнольдса будет равен:
. Применив
соответствующие данные, критерий
Рейнольдса будет равен:
Re
=
 = 3430
= 3430
Поскольку коэффициент Рейнольдса 3430, что больше чем 2300. Следовательно, течение турбулентное.
При таких данных, а это: турбулентное течение и коридорное расположение труб, критерий Нуссельта определяется по формуле:
Nu
=0,26
 (4.14)
(4.14)
где
Pr, – критерий Прандтля для воздуха и стенок
труб соответственно.
– критерий Прандтля для воздуха и стенок
труб соответственно.
Pr
= 0,73 (Приложение А);
 = 0,65. Учитывая эти параметры критерий
Нуссельта равен:
= 0,65. Учитывая эти параметры критерий
Нуссельта равен:
Nu
= 0.26 ∙
 ∙
∙
 ∙
∙
 = 38.6
= 38.6
Коэффициент теплоотдачи можно получить из формулы (4.15), связанную с критерием Нуссельта.
Nu
=
 (4.15)
(4.15)
где
λ
– теплопроводность воздуха,
 .
λ
= 7,8 ∙
.
λ
= 7,8 ∙

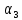 - коэффициент
теплоотдачи, начиная с третьего ряда,
- коэффициент
теплоотдачи, начиная с третьего ряда,

При выводе коэффициент теплоотдачи для третьего и последующих рядов равен:
 = Nu
= Nu = 38,6 ∙
= 38,6 ∙
 = 88,6
= 88,6
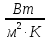 (4.16)
(4.16)
Для первого ряда коэффициент теплоотдачи равен:
 = 0,6
= 0,6
 = 0,6 ∙ 88,6 = 53,1
= 0,6 ∙ 88,6 = 53,1
 (4.17)
(4.17)
Для второго ряда коэффициент теплоотдачи равен:
 = 0,7
= 0,7
 = 0,7 ∙ 88,6 = 62
= 0,7 ∙ 88,6 = 62
 (4.18)
(4.18)
Средний коэффициент теплоотдачи в теплообменнике равен:
 =
=
 =
=
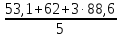 = 76,2
= 76,2
 (4.19)
(4.19)
Выше полученные данные подставляются в формулу (4.8) и определяется удельный поток тепла от первичного теплоносителя к трубам теплообменника:
 = 76,2 ∙
(950-367) = 44424,6
= 76,2 ∙
(950-367) = 44424,6

Подставляем найденные значения в формулу (4.7). Площадь всех труб теплообменника равна:
 =
=
 = 0,25
= 0,25

Длинной одной
трубы необходимо задаться, пусть l
=0,2м. тогда
диаметр одной трубы теплообменника
будет равен:
d
=
 =
=
 = 0.016 м (4.20)
= 0.016 м (4.20)
где d – диаметр одной трубы теплообменника, м;
 – площадь всех
труб теплообменника,
– площадь всех
труб теплообменника,
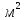 ;
;
π –
l – длинна одной трубы теплообменника, м;
n – количество труб в теплообменнике, шт.

Мощность теплового потока первичного теплоносителя определяется следующим образом:
Ф
=
 (4.21)
(4.21)
где Ф – мощность теплового потока первичного теплоносителя, Вт;
Q – теплота, вносимая с первичным теплоносителем, Дж;
τ – время прохождения теплоты, с.
Для нахождения мощности теплового потока первичного теплоносителя, необходимо найти теплоту, вносимую с первичным теплоносителем. Искомая теплота вычисляется следующим образом:
Q
=
 (4.22)
(4.22)
где
 – теплоёмкость воздуха,
– теплоёмкость воздуха,
 ;
;
 = 1130
= 1130
 ;
;
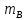 – масса подаваемого
воздуха, кг;
– масса подаваемого
воздуха, кг;
 – начальная
температура наружного воздуха, К.
– начальная
температура наружного воздуха, К.
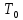 = 243К.
= 243К.
Количество пройденного воздуха за одну секунду определяется по формуле:
 = 3
= 3 ω
= 3 ∙ 1,3 ∙ 0,2 ∙ 12 = 9,36 кг (4.23)
ω
= 3 ∙ 1,3 ∙ 0,2 ∙ 12 = 9,36 кг (4.23)
где
 – плотность воздуха при температуре
243К,
– плотность воздуха при температуре
243К,
 ;
;
 – расстояние между
трубами в ряду, м.
– расстояние между
трубами в ряду, м.
Количество теплоты для нагрева такой массы воздуха определяется по вышеупомянутой формуле (4.22) и равняется:
Q
= 1130 ∙ 9.36 ∙ (1100 – 243) = 9064318Дж = 9,064МДж 
Подставив найденную величину в (4.21), находится тепловая мощность устройства для нагрева первичного теплоносителя и она будет равна:
Ф
=
 = 9,064МВт
= 9,064МВт
