2) Где р является корнем характеристического уравнения

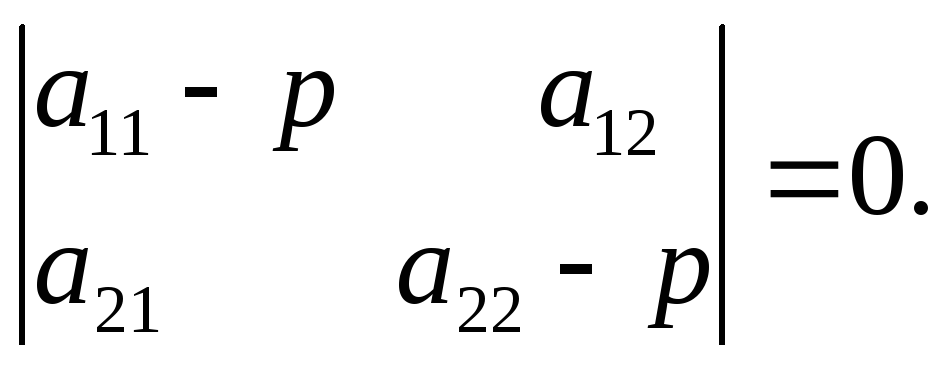
3)Где р является корнем характеристического уравнения

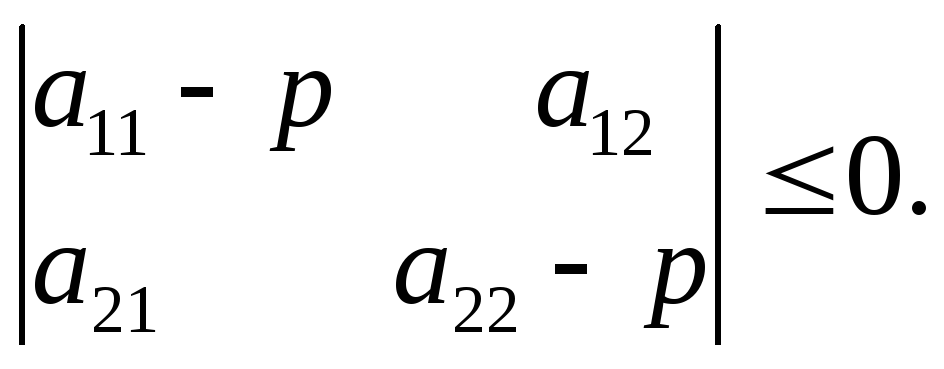
4)Где р является корнем характеристического уравнения

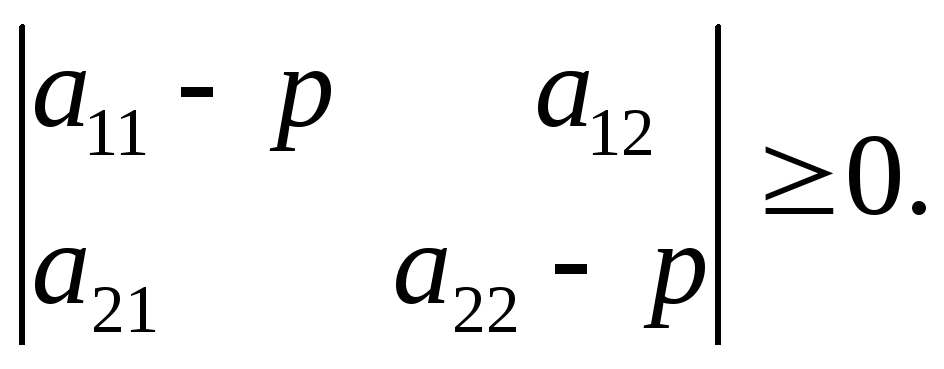
45. Значения р₁ и р₂, полученные из решения уравнения:

:

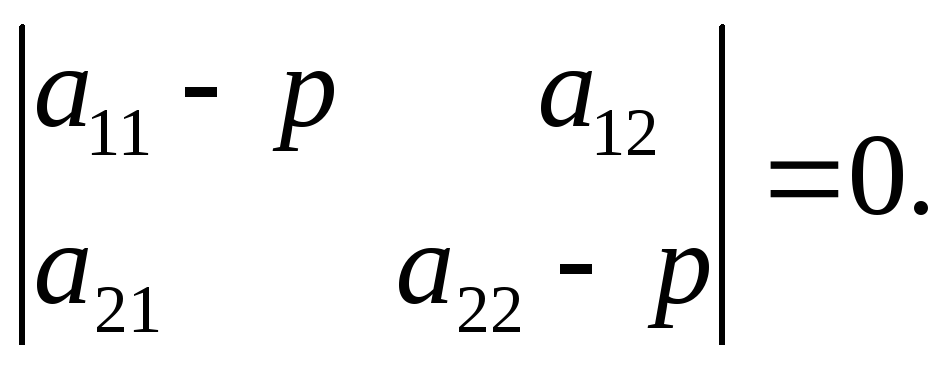1) определяют характер движения вблизи особых точек исходной нелинейной системы , если только ни одно из значений р не обращается в нуль.

2) не определяют характер движения вблизи особых точек исходной нелинейной системы , если только ни одно из значений р не обращается в нуль.

3) определяют характер движения вблизи особых точек исходной нелинейной системы , если только одно из значений р не обращается в нуль.

4) определяют характер движения вблизи особых точек исходной нелинейной системы , если только одно из значений р обращается в нуль.

46. Если дискриминант характеристического уравнения

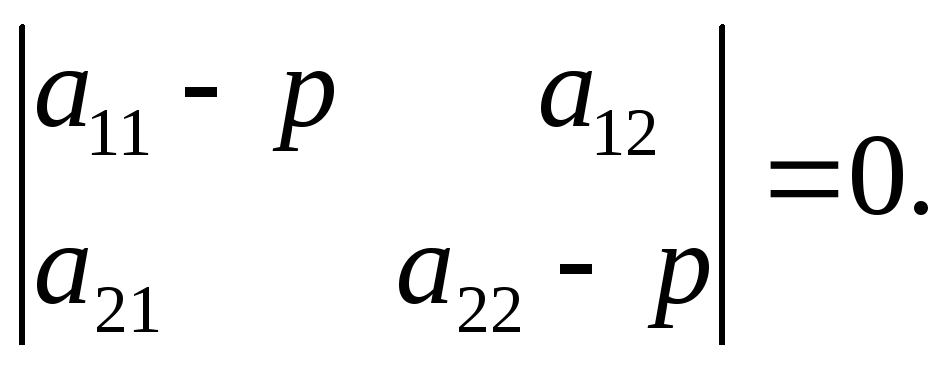
D=4 a₁₂ a₂₁ + (a₁₁ — a₂₂)² 0 , корни р действительны и р₁ < 0, р₂ < 0:

1) решение представляется в виде убывающих экспонент, система, выведенная из положения равновесия, снова стремится к нему, особая точка называется устойчивым узлом.

2) решение представляется в виде возрастающих экспонент, система, выведенная из положения равновесия, снова стремится к нему, особая точка называется устойчивым узлом.

3) решение представляется в виде возрастающих экспонент, система, выведенная из положения равновесия, не стремится к нему, особая точка называется неустойчивым узлом.

4) решение представляется в виде возрастающих экспонент, система, выведенная из положения равновесия, снова стремится к нему, особая точка называется устойчивым фокусом.

47. Если дискриминант характеристического уравнения

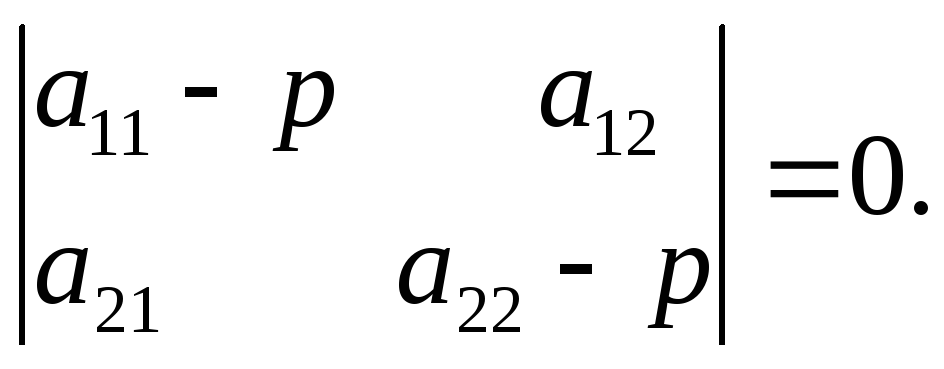
D=4 a₁₂ a₂₁ + (a₁₁ — a₂₂)² 0 , корни р действительны и р₁> 0, р₂ > 0 :

1) решение представляется в виде убывающих экспонент, система, выведенная из положения равновесия, снова стремится к нему, особая точка называется устойчивым узлом.

2) решение представляется в виде возрастающих экспонент, система, выведенная из положения равновесия, снова стремится к нему, особая точка называется устойчивым узлом.

3) решение представляется в виде возрастающих экспонент, система, выведенная из положения равновесия, не стремится к нему, особая точка называется неустойчивым узлом.

4) решение представляется в виде возрастающих экспонент, система, выведенная из положения равновесия, снова стремится к нему, особая точка называется устойчивым фокусом.

48. Если дискриминант характеристического уравнения

D=4 a₁₂ a₂₁ + (a₁₁ — a₂₂)² 0 , корни р действительны и р₁ < 0, р₂ > 0 :

1) особая точка неустойчива и носит название седла, через нее проходят только две интегральные кривые — сепаратрисы, остальные фазовые траектории уходят в бесконечность, минуя особую точку, при этом фазовая плоскость делится сепаратрисами на отдельные участки с одинаковым поведением фазовых траекторий.

2) особая точка устойчива и носит название седла, через нее проходят только две интегральные кривые — сепаратрисы, остальные фазовые траектории уходят в бесконечность, минуя особую точку, при этом фазовая плоскость делится сепаратрисами на отдельные участки с одинаковым поведением фазовых траекторий.

3) особая точка неустойчива и носит название седла, через нее проходят только две интегральные кривые — сепаратрисы, остальные фазовые траектории уходят, проходя через особую точку, в бесконечность, при этом фазовая плоскость делится сепаратрисами на отдельные участки с одинаковым поведением фазовых траекторий.

4) особая точка неустойчива и носит название седла, через нее проходят только две интегральные кривые — сепаратрисы, остальные фазовые траектории уходят в бесконечность, минуя особую точку, при этом фазовая плоскость делится сепаратрисами на отдельные участки с разным поведением фазовых траекторий.

49. Если дискриминант характеристического уравнения

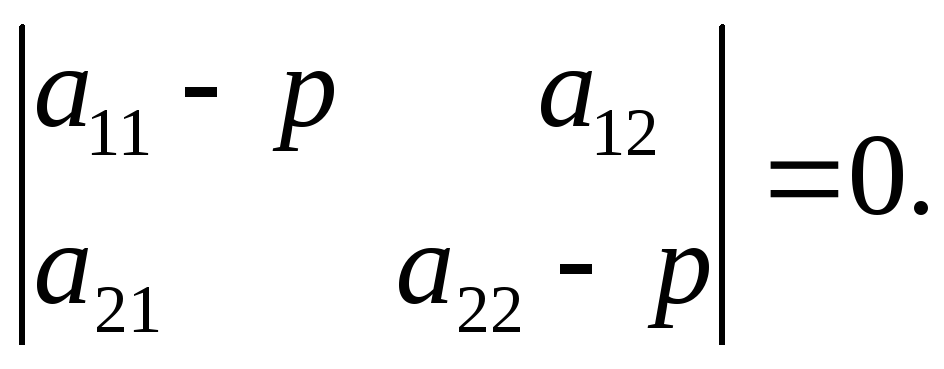
D=4 a₁₂ a₂₁ + (a₁₁ — a₂₂)² < 0 , корни р комплексно-сопряженные, р_1,2 = — и > 0:

1) в системе будут происходить затухающие колебания, на фазовой плоскости это соответствует семейству спиралей, накручивающихся на особую точку, которая носит название устойчивый фокус.

2) в системе будут происходить незатухающие колебания, на фазовой плоскости это соответствует семейству спиралей, накручивающихся на особую точку, которая носит название устойчивый фокус.

3) в системе будут происходить затухающие колебания, на фазовой плоскости это соответствует семейству спиралей, раскручивающихся от особой точки, которая носит название неустойчивый фокус.

4) в системе будут происходить незатухающие колебания, на фазовой плоскости это соответствует семейству спиралей, раскручивающихся от особой точки, которая носит название устойчивый фокус.

50. Если дискриминант характеристического уравнения

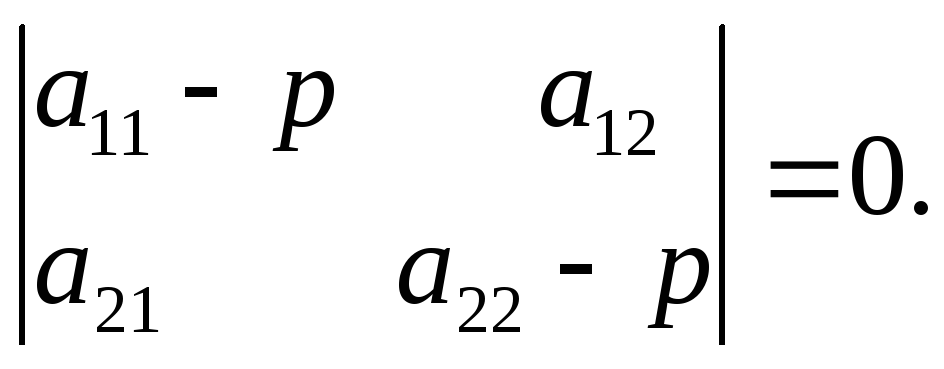
D=4 a₁₂ a₂₁ + (a₁₁ — a₂₂)² < 0 , корни р комплексно-сопряженные, р_1,2 = — и <0 :

1) в системе будут происходить нарастающие по амплитуде колебания, на фазовой плоскости это соответствует семейству спиралей, раскручивающихся от особой точки, которая носит название неустойчивый фокус.

2) в системе будут происходить незатухающие колебания, на фазовой плоскости это соответствует семейству спиралей, накручивающихся на особую точку, которая носит название устойчивый фокус.

3) в системе будут происходить затухающие колебания, на фазовой плоскости это соответствует семейству спиралей, раскручивающихся от особой точки, которая носит название неустойчивый фокус.

4) в системе будут происходить незатухающие колебания, на фазовой плоскости это соответствует семейству спиралей, раскручивающихся от особой точки, которая носит название устойчивый фокус.

51. Если дискриминант характеристического уравнения

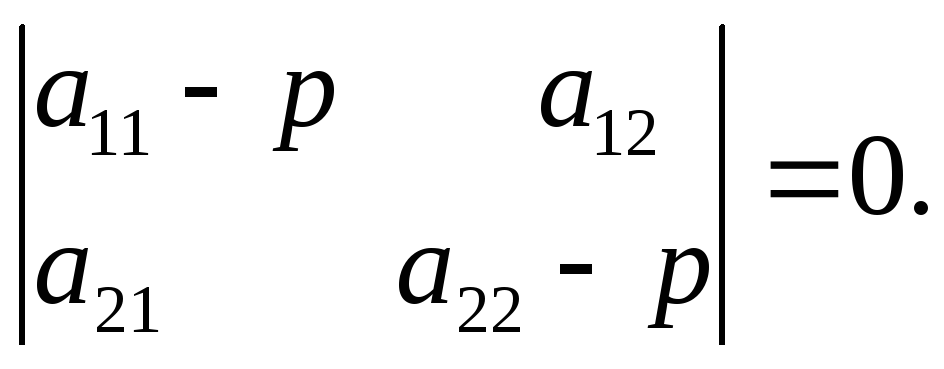
D=4 a₁₂ a₂₁ + (a₁₁ — a₂₂)² < 0 , корни р комплексно-сопряженные, р_1,2 = — и = 0:

1) в системе будут происходить незатухающие колебания, на фазовой плоскости это соответствует семейству вложенных друг в друга эллипсов, особая точка носит название центра.

2) в системе будут происходить незатухающие колебания, на фазовой плоскости это соответствует семейству спиралей, накручивающихся на особую точку, которая носит название устойчивый фокус.

3) в системе будут происходить затухающие колебания, на фазовой плоскости это соответствует семейству спиралей, раскручивающихся от особой точки, которая носит название неустойчивый фокус.

4) в системе будут происходить незатухающие колебания, на фазовой плоскости это соответствует семейству спиралей, раскручивающихся от особой точки, которая носит название устойчивый фокус.

52. Форма предельного цикла при гармонических колебаниях в системе имеет:

1) эллиптическую форму.

2) треугольную форму.

3) прямоугольную форму.

4) более сложную форму.

53. Форма предельного цикла при релаксационных колебаниях в системе имеет:

1) эллиптическую форму.

2) только треугольную форму.

3) только прямоугольную форму.

4) треугольную форму, прямоугольную форму, более сложную форму.