
лабораторная работа / Комлева / ТАУ3
.docЦель работы: Изучение графической операционной среды системы MatLab. Получение навыков работы в системе MatLab при выполнении вычислительных операций.
Выполнение работы
-
Дана система уравнений:
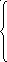
![]()
![]()
![]()
![]()
Сформируем из данной системы уравнений матрицу коэффициентов А и матрицу свободных членов В и найдем вектор корней системы уравнений:
>> A=[2 2 6 1;0 -1 2 1;4 -3 1 -5;3 -5 1 -1]
A =
2 2 6 1
0 -1 2 1
4 -3 1 -5
3 -5 1 -1
>> B=[15;18;37;30]
B =
15
18
37
30
>> x=A\B
x =
-8.1429
-7.5714
9.0000
-7.5714
Выполним заданные операции с вектором:
>> disp(B')
15 18 37 30
>> disp(B*7)
105
126
259
210
>> disp(B+7)
22
25
44
37
>> disp(B.^7)
1.0e+010 *
0.0171
0.0612
9.4932
2.1870
Выполним заданные операции с матрицей:
>> disp(A')
2 0 4 3
2 -1 -3 -5
6 2 1 1
1 1 -5 -1
>> disp(A^7)
65880 -4037 87199 -64198
18673 -15724 14133 -18409
15383 36930 29274 -19256
26558 13132 31899 -29204
>> disp(inv(A))
0.2857 -0.9660 -0.2245 0.4422
0.1429 -0.3878 -0.0408 -0.0408
-0.0000 0.5238 0.1429 -0.1905
0.1429 -0.4354 -0.3265 0.3401
>> disp(expm(A))
114.6421 43.0216 165.0397 -108.5857
21.6571 8.5302 31.5571 -20.9901
40.7145 19.3438 62.0073 -43.0498
46.8006 14.9055 65.1125 -41.4988
>> disp(logm(A))
-0.0435 4.8703 1.5195 0.4308
-1.0493 3.2749 0.7637 1.1285
1.5441 -4.4821 0.9883 -1.1818
0.2044 -1.0680 0.9336 0.7707
>> disp(sqrtm(A))
0.7752 + 0.0000i 2.8940 + 0.0000i 1.6987 - 0.0000i 0.7157 - 0.0000i
-0.6065 + 0.0000i 2.1321 - 0.0000i 0.7601 - 0.0000i 0.8648 - 0.0000i
1.5848 + 0.0000i -3.0632 - 0.0000i 1.2313 + 0.0000i -1.6065 - 0.0000i
0.6459 + 0.0000i -1.6909 - 0.0000i 0.5477 + 0.0000i 0.9381 - 0.0000i
-
Вычислим функции линейной алгебры:
>> disp(cond(A))
12.7386
>> disp(norm(A))
8.8283
>> disp(rcond(A))
0.0393
>> disp(rank(A))
4
>> disp(det(A))
147
>> disp(trace(A))
1
>> disp(null(A))
>> disp(orth(A))
-0.1123 -0.9615 0.1190 0.2209
-0.0689 -0.2444 -0.4482 -0.8571
-0.7729 0.1000 0.5685 -0.2636
-0.6207 0.0765 -0.6796 0.3835
>> disp(rref(A))
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
-
Дан полином:
![]()
Для вычисления корней полинома сформируем вектор коэффициентов заданного полинома и вычислим корни с помощью функции roots(p):
>> p=[1 3 -23 -55 -150]
p =
1 3 -23 -55 -150
>> r=(roots(p))
r =
5.0000
-6.0000
-1.0000 + 2.0000i
-1.0000 - 2.0000i
Для определения коэффициентов полинома воспользуемся функцией poly(r):
>> poly(r)
ans =
-
3.0000 -23.0000 -55.0000 -150.0000
Вычислим значение заданного полинома по значению аргумента, используя функцию polyval:
>> disp(polyval(p,3))
-360
Вычислим значение коэффициентов производной заданного полинома:
>> disp(polyder(p))
4 9 -46 -55
-
Дана функция:
![]()
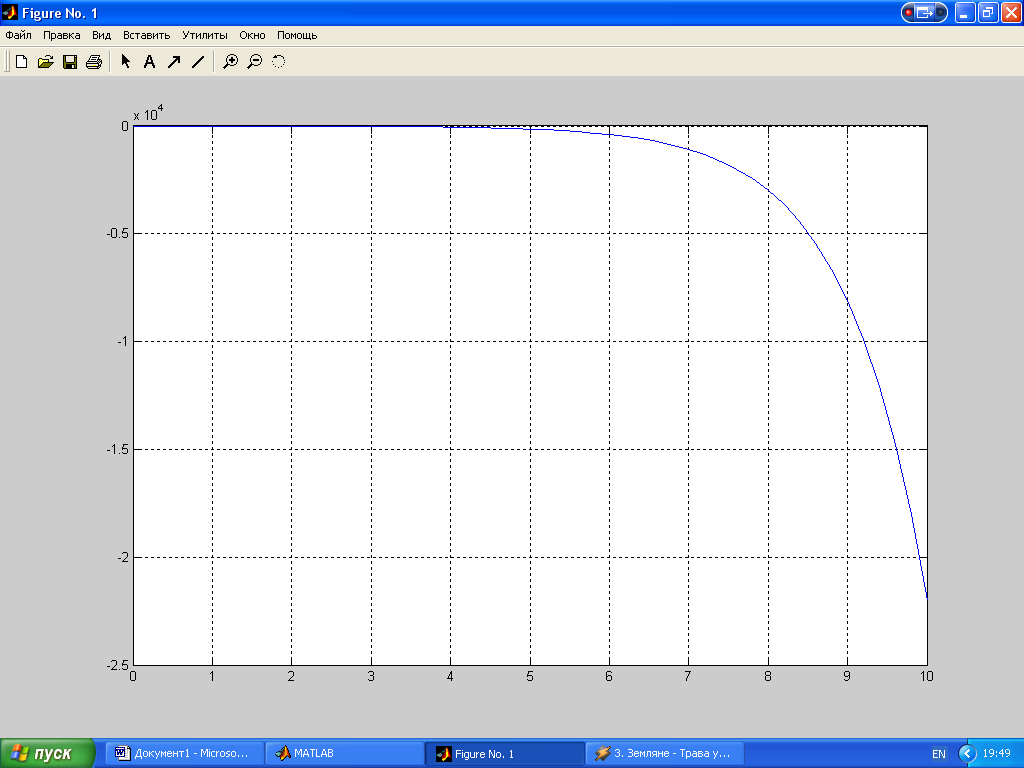
Для построения графика заданной функции зададим диапазон изменения аргумента х, запишем заданную функцию и воспользуемся функцией plot:
>> x=0:0.2:10;
>> y=cos(x.^3+2)-exp(x);
>> plot(x,y);grid
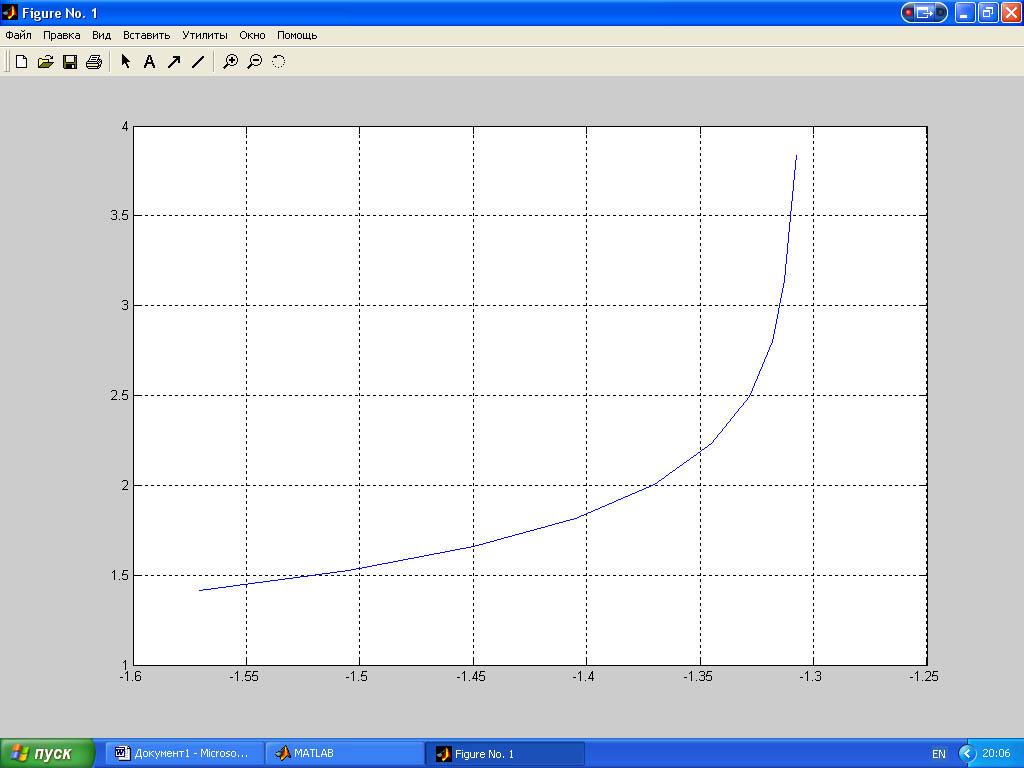
Для построения графика в полярной системе координат преобразуем декартовые координаты в полярные:
>> x=0:0.1:1;
>> y=cos(x.^3+2)-exp(x);
>> [TH,R]=cart2pol(x,y);
>> plot(TH,R);grid
-
Дана передаточная функция:
![]()
Для построения частотных характеристик воспользуемся последовательностью действий:
>> P1=[3 0 -5]; P2=[-6 -1 -2 -3];
>> roots(P1);
>> roots(P2);
>> om0=1e-2; omk=1e2;
>> OM=logspace(-2,2,41);p=j*OM;
>> ch=polyval(P1,p);zn=polyval(P2,p);
>> ACH=abs(ch)./abs(zn);
>> FCH=angle(ch./zn)*180/pi;
>> subplot(2,1,1);
>> loglog(OM,ACH);grid
>> figure, semilogx(OM,FCH);grid
>> loglog(OM,ACH);grid
>> figure, semilogx(OM,FCH);grid

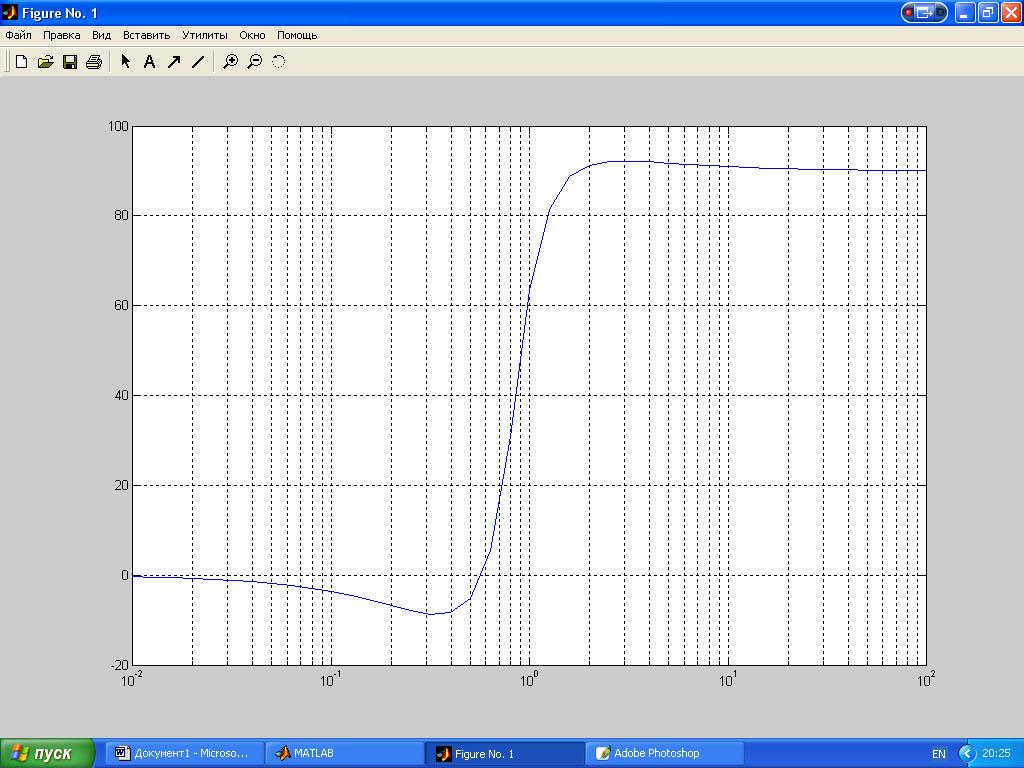
Вывод: В результате проделанной работы я ознакомился с возможностями системы MatLab, получил необходимые навыки работы в этой системе.
