Министерство образования Российской Федерации

Саратовский государственный технический университет

ИЗУЧЕНИЕ ГРАФИЧЕСКОЙ ОПЕРАЦИОННОЙ СРЕДЫ СИСТЕМЫ MATLAB

Методические указания к лабораторной работе по курсу «Теория автоматического управления» для студентов специальности 210100

Одобрено редакционно-

издательским советом

Саратовского государственного

технического университета

Саратов 2004

Цель работы: Изучение графической операционной среды системы MATLAB. Получение навыков работы в системе MATLAB при выполнении вычислительных операций.

ОСНОВНЫЕ ПОНЯТИЯ

Система MATLAB создана для проведения инженерных расчетов. Данная система содержит множество процедур и функций, необходимых инженеру для осуществления сложных численных расчетов, моделирования технических и физических систем и оформления результатов этих расчетов. Математический аппарат этой системы основывается на вычислениях, проводимых с матрицами, векторами и комплексными числами. Система позволяет выполнять различные операции с векторами, матрицами и массивами данных, реализует сингулярное и спектральное разложение, расчет ранга и чисел обусловленности матриц, поддерживает работу с алгебраическими полиномами, решение нелинейных уравнений и задач оптимизации, интегрирование функций, численное интегрирование дифференциальных и разностных уравнений, построение различных графиков, трехмерных поверхностей и линий уровня.

Работать в системе MATLAB можно как в режиме калькулятора, так и в программном режиме. При работе в первом из них вычисления осуществляются сразу после набора очередного оператора или команды, результаты вычислений могут присваиваться некоторым переменным, либо получаются непосредственно, без использования операций присваивания. Работа в программном режиме осуществляется путем вызова имени написанной на языке MATLAB программы, предварительно составленной и записанной на диске.

При запуске системы по умолчанию открывается три окна: окно команд, рабочая область, команды. Окно MATLAB представлено на рисунке 1.

Рисунок 1 – Окно MATLAB

Кроме вышеперечисленных окон есть еще два окна: Текущий каталог и Запустить Редактор. Для активизации этих окон необходимо открыть меню Вид главного меню и выбрать название необходимого окна. Кроме того, здесь можно изменить состав и размещение окон рабочего стола, для чего необходимо выбрать подменю Схема Рабочего Стола, которая имеет шесть опций. Меню Вид и подменю Схема Рабочего стола изображена на рисунке 2.

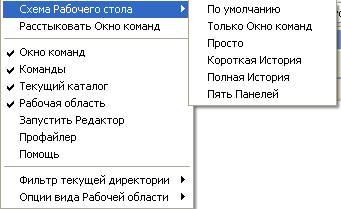
Рисунок 2 – Меню Вид системы MATLAB

Например, если активизировать опцию Пять Панелей, то рабочий стол примет вид, показанный на рисунке 3.

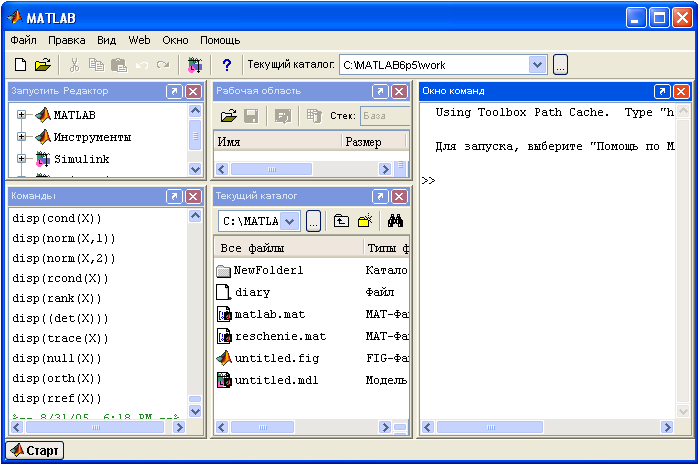
Рисунок 3 – Рабочий стол в режиме опции Пять Панелей.

Для изменения свойств рабочего стола используется подменю Предпочтения, расположенное в меню Файл. При активизации этой опции на экране появится окно Предпочтения, Изображенное на рисунке 4. Окно содержит дерево опций, относящихся к различным окнам рабочего стола.

Первая опция – Основное используется для оформления рабочего стола, организации кэш-памяти при работе с ППП, организации вывода на печать, выбора шрифтов и управления файлами.

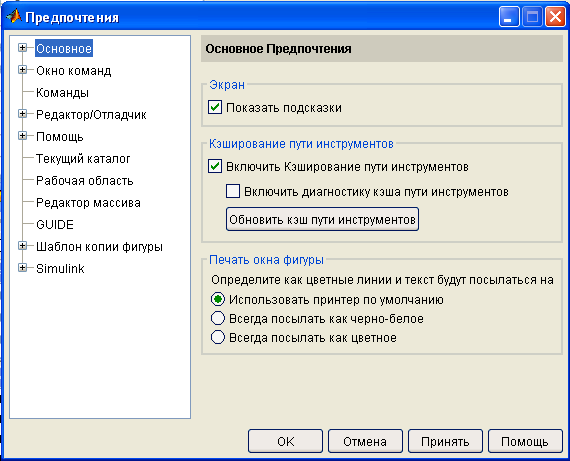
Рисунок 4 – Окно Предпочтения системы MATLAB

Для настройки типа и размера шрифта, цвета текста, вводимого с командной строки, следует воспользоваться опцией Шрифт & Цвета. Другой компонент настройки Контроль источника – это система управления файлами, которая позволяет отслеживать все изменения, обеспечивая интерфейс с системой управления файлами.

Окно Запустить редактор предназначено для вызова программных продуктов, входящих в состав установленной версии системы MATLAB. Контекстное меню этой панели (рисунок 5) содержит опции: Открыть, Просмотреть исходник, Обновить.

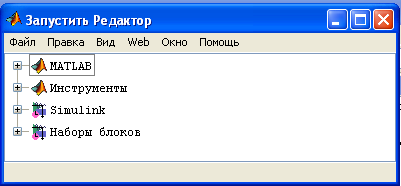
Рисунок 5 – Окно Запустить редактор

Командное окно, показанное на рисунке 6, предназначено для работы с переменными, файлами и функциями системы MATLAB в режиме командной строки.

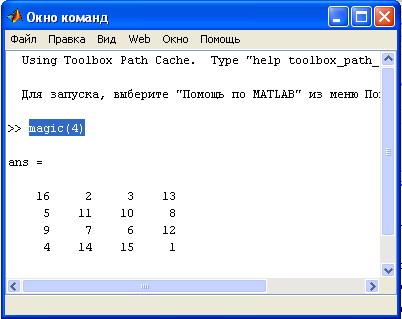
Рисунок 6 – Панель Окно Команд

Для командного окна предусмотрен специальный набор настроек, которые управляют форматом вывода чисел, включают режим вывода на экран исполняемых операторов, регулируют размеры шрифта и цвета. Данные настройки расположены в меню Предпочтения: опции Шрифт & Цвета и Клавиатура & Отступы Окна команд – рисунок 7.

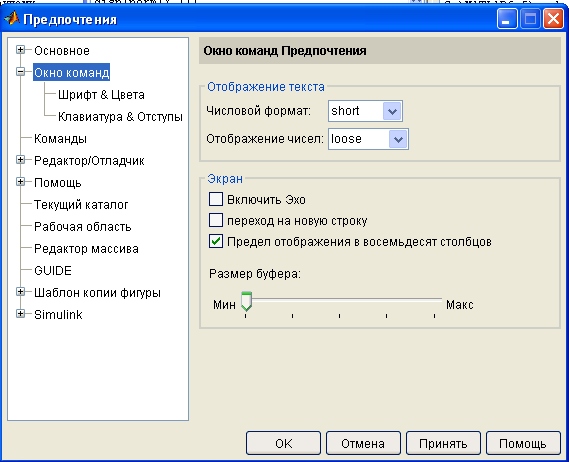
Рисунок 7 – Окно Предпочтения с активной опцией Окно команд

Набор настроек Отображение текста позволяет управлять следующими параметрами. Числовой формат – формат вывода чисел в командное окно. Соответствующий список включает в себя следующие форматы вывода:

- short – краткая запись в формате с фиксированной запятой;

- long – длинная запись в формате с фиксированной запятой;

- short e – краткая запись в формате с плавающей запятой;

- long e – длинная запись в формате с плавающей запятой;

- short g – вторая форма краткой записи в формате с плавающей запятой;

- long g – вторая форма длинной записи в формате с плавающей запятой;

- hex – запись в виде шестнадцатеричного числа;

- bank – запись до сотых долей

- + - записывается только знак числа;

- rational – запись в виде рациональной дроби.

Отображение чисел – опция управления пробелом между строками; значение compact подавляет, значение loose восстанавливает пробел между строками.

Окно Команды, рисунок 8, фиксирует дату и время начала сеанса работы с системой, а также строки операторов, которые вводятся в командном окне с начала сеанса работы. Для изменения установок данной панели используется опция Команды панели Предпочтения из меню Файл.

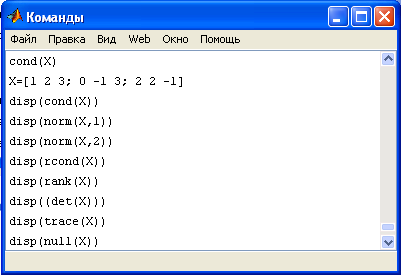
Рисунок 8 – Окно Команды

Окно Рабочая область, показанное на рисунке 9, содержит список переменных, накопленных в рабочей памяти системы в процессе сеанса работы.

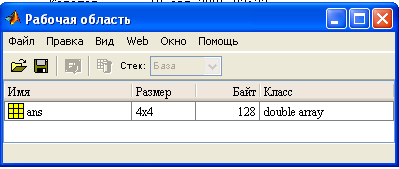
Рисунок 9 – Панель Рабочая область.

Для каждой переменной указывается размер массива, объем памяти и класс. Выводом этой информации в окно рабочей области можно управлять с помощью опций подменю Опции вида Рабочей области меню Вид. После завершения работы, данные в рабочей области не сохраняются, необходимо предусмотреть их запись в виде файла с расширением .mat. Настройка параметров для этого окна осуществляется с помощью опции Рабочая область панели Предпочтения меню Файл. Она позволяет изменить шрифт окна.

Окно рабочей области позволяет выполнять также функцию обозревателя данных. Для этого необходимо вызвать редактор данных Array Editor с помощью двойного щелчка по левой клавиши мыши. На рисунке 10 показан редактор данных, который позволяет в интерактивном режиме просматривать и корректировать одномерные и двумерные числовые массивы, массивы строк и массивы строковых ячеек. Настройки параметров панели Array Editor используются опции Редактора массива панели Предпочтения.

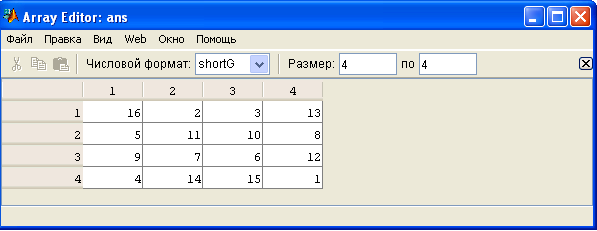
Рисунок 10 – Панель редактора данных

При работе с файлами в системе MATLAB текущий каталог выполняет роль точки отсчета. Любой файл, к которому нужно обратиться, должен размещаться либо в текущем каталоге, либо на пути доступа. Окно просмотра текущего каталога показано на рисунке 11.

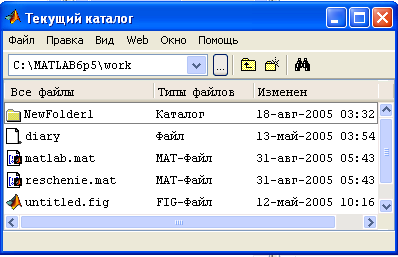
Рисунок 11 – Панель Текущий каталог

Для настройки параметров окна Текущий каталог используются опции Текущего каталога панели Предпочтения меню Файл. При нажатии кнопки Найти меню Правка в окне Текущий каталог откроется панель, изображенная на рисунке 12, с помощью которой можно осуществить поиск интересующего файла.

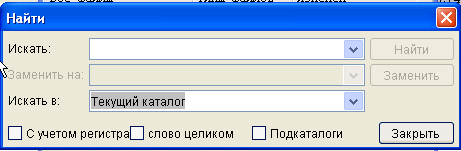
Рисунок 12 – Панель поиска

В состав MATLAB 6 входят мощная подсистема справки и обширная демонстрационная система. Окно справочной системы показано на рисунке 13. Оно делится на две области: область навигации и область просмотра. В Навигаторе помощи пользователь может указать интересующую тему, термин или функцию, а в области просмотра ознакомиться с найденной информацией.

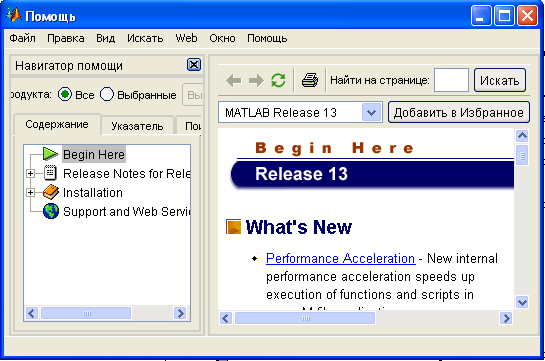
Рисунок 13 – Окно справочной системы MATLAB

Операции с числами

Главными объектами MATLAB являются числа. Операции с ними лежат в основе работы с системой. Ввод действительных чисел с клавиатуры осуществляется по общим правилам: для отделения дробной части мантиссы числа используется десятичная точка; десятичный показатель числа записывается целым числом после символа е; между записью мантиссы числа и символа е не должно быть других символов, в том числе и символа пробела.

Например: >> 1.20357661e-17

ans =

1.2036e-017

Формат числа, отображенного на экране, обусловлено соответствующей опцией числовой формат панели Предпочтения меню Файл. Для выполнения простых вычислений необходимо в командную строку ввести последовательность чисел и знаков арифметических операций. Для получения результатов вычислений необходимо после ввода выражения нажать клавишу Enter, в командном окне под именем системной переменной ans будет выведен результат выполнения последнего оператора.

Например: >> 4.5^2*7.23-3.14*10.4

ans =

113.7515

В системе MATLAB несколько последних команд запоминаются. Повторный вызов этих команд в командном окне осуществляется путем нажатия клавиш ↑ и ↓. В арифметических выражениях языка MATLAB применяются знаки операций, приведенные в таблице 1.

Таблица 1. Знаки операций

Знак операции	Выполняемое действие	Знак операции	Выполняемое действие
+	Сложение	/	Деление слева направо
-	Вычитание	\	Деление справа налево
*	Умножение	^	Возведение в степень

Вывод промежуточной информации в командное окно подчиняется следующим правилам:

- если запись оператора не заканчивается символом «;», результат действия этого оператора сразу же выводиться в командное окно;

- если оператор заканчивается символом «;», результат его действия не отображается в командном окне;

- если оператор не содержит знака присваивания «=», то значение результата присваивается специальной системной переменной ans;

- значение системной переменной ans можно использовать в последующих операторах вычислений, путем указания её имени; при этом необходимо помнить, что значение этой переменной после выполнения очередного оператора, не содержащего знака присваивания, изменяется. Если использовать функцию disp, которая выводит в командное окно результаты расчетов или текст, то результат будет выводиться без переменной ans.

Например:

>> 25+17 ans = 42 >> ans*7 ans = 294 >>

>> 25+17; >> ans*7 ans = 294 >>

>> disp(2+3) 5 >>

Для записи промежуточных результатов в память компьютера можно применять имена переменных. С этой целью выполняется операция присваивания. Выражение, которое находиться справа от знака присваивания, может быть числом, арифметическим выражением, строкой символов или символьным выражением. Если выражение не заканчивается знаком «;», после нажатия клавиши Enter в командном окне отобразится результат выполнения. Имя переменной может содержать до 30 символов и не должно совпадать с именами функций, процедур и системных переменных. При этом различаются прописные и строчные буквы. В системе MATLAB имеются зарезервированные именованные константы и переменные, которые можно использовать в математических выражениях (таблица 2).

Таблица 2. Имена зарезервированных констант и переменных

Имя	Значение
i, j	Мнимая единица
Pi	Число π
inf	Обозначение машинной бесконечности
NaN	Обозначение неопределенного результата
eps	Погрешность операций над числами с плавающей запятой
ans	Результат последней операции без знака присваивания
realmax realmin	Максимально и минимально возможные значения, которые могут быть использованы в системе

В MATLAB для обращения к функции используется форма:

ИМЯ РЕЗУЛЬТАТА=ИМЯ ФУНКЦИИ(ПЕРЕЧЕНЬ АРГУМЕНТОВ).

В таблицах 3 и 4 представлены математические функции, предусмотренные в MATLAB.

Таблица 3. Элементарные математические функции

Функция	Описание
Тригонометрические и гиперболические
sin(z)	Синус числа
sinh(z)	Гиперболический синус
asin(z)	Арксинус (в диапазоне от –π/2 до π/2 ), выраженный в радианах
asinh(z)	Обратный гиперболический синус
cos(z)	Косинус
cosh(z)	Гиперболический косинус
acos(z)	Арккосинус (от 0 до π)
acosh(z)	Обратный гиперболический косинус
tan(z)	Тангенс
tanh(z)	Гиперболический тангенс
atan(z)	Арктангенс (от –π/2 до π/2)
atan2(x,y)	Четырехквадрантный арктангенс
atanh(z)	Обратный гиперболический тангенс
sec(z)	Секанс
sech(z)	Гиперболический секанс
asec(z)	Арксеканс
asech(z)	Обратный гиперболический секанс
csc(z)	Косеканс
csch(z)	Гиперболический косеканс
acsc(z)	Арккосеканс
acsch(z)	Обратный гиперболический косеканс
cot(z)	Котангенс
coth(z)	Гиперболический котангенс
acot(z)	Арккотангенс
acoth(z)	Обратный гиперболический котангенс
Экспоненциальные функции
exp(z)	Экспонента числа
log(z)	Натуральный логарифм
log10(z)	Десятичный логарифм
sqrt(z)	Квадратный корень из числа
abs(z)	Модуль числа
Целочисленные функции
fix(z)	Округление до ближайшего целого числа в сторону 0
floor(z)	Округление до ближайшего целого в сторону -∞
ceil(z)	Округление до ближайшего целого в сторону +∞
round(z)	Обычное округление до ближайшего целого
mod(x,y)	Целочисленное деление x на y
rem(x,y)	Вычисление остатка от деления x на y
sign(z)	Вычисление сигнум-функции числа

Таблица 4. Специальные математические функции

Функция	Описание
Функции преобразования координат
cart2sph	Преобразование декартовых координат в сферические
art2pol	Преобразование декартовых координат в полярные
pol2cart	Преобразование полярных координат в декартовы
sph2cart	Преобразование сферических координат в декартовы
Функции Бесселя
besselj	Функция Бесселя первого рода
bessely	Функция Бесселя второго рода
besseli	Модифицированная функция Бесселя первого рода
besselk	Модифицированная функция Бесселя второго рода
Бета-функции
beta	Бета-функция
betainc	Усеченная бета-функция
betaln	Логарифм бета-функции
Гамма-функции
gamma	Гамма-функция
gammainc	Усеченная гамма-функция
gammaln	Логарифм гамма-функции
Эллиптические функции и интегралы
ellipj	Эллиптические функции Якоби
ellipke	Полный эллиптический интеграл
expint	Функция экспоненциального интеграла
Функции ошибок
erf	Функция ошибок
erfc	Дополнительная функция ошибок
erfcx	Масштабированная дополнительная функция ошибок
erfinv	Обратная функция ошибок
Другие функции
gcd	Наибольший общий делитель
lcm	Наименьшее общее кратное
legendre	Обобщенная функция Лежандра
log2	Логарифм по основанию 2
pow2	Возведение числа 2 в указанную степень
rat	Представление числа в виде рациональной дроби
rats	Представление чисел в виде рациональной дроби

Язык системы MATLAB позволяет выполнять различные операции с комплексными числами. Для обозначения мнимой единицы зарезервированы два имени i и j. На экран система выводит комплексные числа в виде:

>> x=1+i*2

x =

1.0000+2.0000i

Простейшие действия с комплексными числами – сложение, вычитание, умножение, деление, возведение в степень (+, -, *, /, \, ^).

Дополнительные функции, рассчитанные только на применение комплексного аргумента, представлены в таблице 5.

Таблица 5. Функции комплексного аргумента

Функция	Описание
real(z)	Выделяет действительную часть комплексного аргумента
imag(z)	Выделяет мнимую часть комплексного аргумента
angle(z)	Вычисляет значение аргумента комплексного числа в диапазоне от –π до +∞ (в радианах)
conj(z)	Выделяет число, комплексно сопряженное относительно z