
- •Операции с числами
- •Операции с векторами и матрицами
- •Функции прикладной численной математики
- •Построение графиков
- •Задание к лабораторной работе
- •Пример выполнения работы
- •Время, отведенное на лабораторную работу
- •Методические указания к лабораторной работе по курсу «Теория автоматического управления» для студентов специальности 210100
- •410054, Г. Саратов, ул. Политехническая, 77
Задание к лабораторной работе
-
Ознакомиться с основными элементами теории.
-
Запустить систему MATLAB.
-
Решить систему уравнений в соответствии с вариантом таблицы Б. Сформировать матрицу из коэффициентов данной системы уравнений и вектор из свободных членов системы. Для полученного вектора выполнить следующие операции: транспонирование, умножение вектора на число, равное номеру варианта, прибавить к каждому элементу вектора данное число, осуществить поэлементное возведение в степень данного числа полученный вектор. Для матрицы выполнить: транспонирование, обращение матрицы, возведение матрицы в степень числа, равного номеру варианта, вычислить матричную экспоненту, выполнить логарифмирование матрицы, вычислить корень.
-
Вычислить функции линейной алгебры: cond(А), norm(v,p), recond(A), rank(А), det(A), trace(A), null(A), orth(A), rref(A).
-
Вычислить корни полинома в соответствии с вариантом таблицы А. Выполните обратное действие: определите коэффициенты полинома по вычисленным корням. Определить значение полинома по заданному аргументу (в качестве аргумента принять число, равное номеру варианта). Определить значение коэффициентов производной заданного полинома.
-
Построить графики функций, в соответствии с вариантом таблицы В в декартовой и полярной системах координат.
-
Для передаточной функции
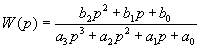 построить
АЧХ и ФЧХ заданной частотной передаточной
функции в соответствии с вариантом
таблицы Г. Постройте эти графики в одном
графическом окне.
построить
АЧХ и ФЧХ заданной частотной передаточной
функции в соответствии с вариантом
таблицы Г. Постройте эти графики в одном
графическом окне. -
Оформить отчет.
Пример выполнения работы
-
Сформируем из данной системы уравнений матрицу коэффициентов А и матрицу свободных членов В и найдем вектор корней системы уравнений:
>> A=[1 2 3; 2 -1 -5; 1 -1 -1]
A =
1 2 3
2 -1 -5
1 -1 -1
>> B=[14;-15;-4]
B =
14
-15
-4
>> x=A\B
x =
1.0000
2.0000
3.0000
Выполним заданные операции с вектором:
>> disp(B')
14 -15 -4
>> disp(B*3)
42
-45
-12
>> disp(B+3)
17
-12
-1
>> disp(B.^3)
2744
-3375
-64
Выполним заданные операции с матрицей:
>> disp(A')
1 2 1
2 -1 -1
3 -5 -1
>> disp(inv(A))
0.3077 0.0769 0.5385
0.2308 0.3077 -0.8462
0.0769 -0.2308 0.3846
>> disp(A^3)
-8 29 49
31 -36 -81
15 -17 -35
>> disp(expm(A))
7.7547 4.0014 1.6079
2.4035 2.9544 -3.2125
1.6012 -0.0034 2.1555
>> disp(logm(A))
0.9584 + 0.5908i -0.0223 - 0.8050i -0.6843 - 1.6488i
-0.2590 - 0.9655i 0.8624 + 1.3155i 1.0617 + 2.6945i
-0.0703 - 0.4426i 0.3070 + 0.6031i 0.7441 + 1.2353i
>> disp(sqrtm(A))
1.2276 + 0.3996i 0.4860 - 0.5445i 0.5784 - 1.1153i
0.4312 - 0.6531i 0.7142 + 0.8899i -0.9822 + 1.8227i
0.2293 - 0.2994i -0.1745 + 0.4080i 0.6868 + 0.8356i
-
Вычислим функции линейной алгебры:
>> X=[1 2 3; 0 -1 3; 2 2 -1]
X =
1 2 3
0 -1 3
2 2 -1
>> disp(cond(X))
5.3605
>> disp(norm(X,1))
7
>> disp(norm(X,2))
4.3963
>> disp(rcond(X))
0.1092
>> disp(rank(X))
3
>> disp((det(X)))
13
>> disp(trace(X))
-1
>> disp(null(X))
>> disp(orth(X))
-0.7774 -0.4082 0.4786
-0.6244 0.4082 -0.6659
0.0765 -0.8165 -0.5723
>> disp(rref(X))
1 0 0
0 1 0
0 0 1
-
Для вычисления корней полинома сформируем вектор коэффициентов заданного полинома и вычислим корни с помощью функции roots(p):
>> p=[1 -2 1 -12 20];
>> r=(roots(p))
r =
-1.0000 + 2.0000i
-1.0000 - 2.0000i
2.0000
2.0000
Для определения коэффициентов полинома воспользуемся функцией poly(r):
>> disp(poly(r))
1.0000 -2.0000 1.0000 -12.0000 20.0000
Вычислим значение заданного полинома по значению аргумента, используя функцию polyval:
>> disp(polyval(p,3))
20
Определим значение коэффициентов производной заданного полинома:
>> disp(polyder(p))
4 -6 2 -12
-
Для построения графика заданной функции зададим диапазон изменения аргумента х, запишем заданную функцию и воспользуемся функцией plot:
>> x=0:0.1:10;
>> y=x-4*sqrt(x)+3;
>> plot(x,y);grid
Для построения графика в полярной системе координат необходимо преобразовать декартовые координаты в полярные:
>> x=0:0.1:1;
>> y=x-4*sqrt(x)+3;
>> [TH,R] = cart2pol(x,y);
>> plot(TH,R),grid
-
Для построения частотных характеристик воспользуемся последовательностью действий:
>> P1 = [1 4]; P2 = [1 4 100];
>>roots(P1);
>>roots(P2);
>>om0=1e-2; omk=1e2;
>>OM=logspace(-2,2,41); p=i*OM;
>>ch=polyval(P1,p);zn=polyval(P2,p);
>> ACH=abs(ch)./abs(zn);
>>FCH=angle(ch./zn)*180/pi;
>> subplot(2,1,1);
>>loglog(OM,ACH);grid
>>figure, semilogx(OM,FCH); grid
СОДЕРЖАНИЕ ОТЧЕТА
Отчет оформляется в соответствии с требованиями, предъявляемыми к оформлению работ в вузе, и должен содержать:
-
Титульный лист
-
Наименование и цель работы.
-
Результаты выполнения работы.
-
Анализ результатов и выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Каким образом представляются действительные числа при вычислениях в системе MATLAB?
-
Как можно изменить формат представления действительных чисел в командном окне?
-
Каким образом объявляются переменные в языке MATLAB?
-
Как добиться того, чтобы результат действий, записанных в очередной строке: а) выводился в командное окно; б) не выводился в командное окно?
-
Какую роль играет системная переменная ans?
-
Как возвратить в командную строку ранее введенную команду?
-
Как ввести значение комплексного числа и в каком виде оно будет выведено на экран?
-
Как в языке MATLAB обеспечить сложение, вычитание, умножение, деление и возведение в степень комплексных чисел?
-
Какие функции работы с комплексными числами предусмотрены в языке MATLAB?
-
Как вводятся векторы в языке MATLAB? С помощью каких функций можно формировать векторы?
-
Какие функции позволяют преобразовать векторы поэлементно?
-
С помощью каких средств осуществляются основные операции с векторами?
-
Как вводятся матрицы в системе MATLAB?
-
Как сформировать матрицу: а) по заданным векторам ее строк; б) по заданным векторам ее столбцов; в) по заданным векторам ее диагоналей?
-
Какие функции осуществляют поэлементное преобразование матриц?
-
как осуществляются обычные матричные операции?
-
Как можно решить систему алгебраических уравнений?
-
Какой объект в MATLAB называется полиномом?
-
Как осуществляется умножение и деление полиномов?
-
С помощью каких функций можно найти: а) корни заданного полинома; б) значение полинома по известному значению аргумента?
-
Какие функции позволяют найти производную от полинома?
-
Как найти характеристический полином матрицы?
-
Какие функции MATLAB осуществляют вывод графиков на экран?
-
Какие функции позволяют обеспечить снабжение графика координатными линиями и надписями?
-
Как выводиться график в виде столбцовой диаграммы?
-
Как можно построить гистограмму в MATLAB?
-
Можно ли построить несколько графиков в одной системе координат и в одном графическом окне?
-
Каким образом можно вывести несколько отдельных графиков в разных графических окнах?
-
Как построить несколько оnдельных графиков: а) в одном графическом окне; б) в разных графических полях?
-
Какие средства управления ходом вычислительного процесса предусмотрены в языке MATLAB?
-
Как можно организовать вычисления по циклу?
-
Как организовать вывод в командное окно MATLAB таблицы с результатами вычислений?
