5.1 Вопросы для самопроверки

1. Как выделить целую часть у неправильной рациональной дроби?

2. Какие виды правильных рациональных дробей Вы знаете?

3. Как разлагаются правильные рациональные дроби на простейшие?

4. Как найти неопределенные коэффициенты А,В,С… в случае некратных линейных сомножителей знаменателя?

5. С чего начинать нахождение неопределенных коэффициентов в случае кратных линейных сомножителей знаменателя? Как найти остальные коэффициенты?

5.2 Примеры для самостоятельного решения

1. , 2. ,

3. , 4. .

6 Интегрирование тригонометрических функций Рассмотрим интегралы вида

,

когда в числителе и знаменателе могут присутствовать целые степени и .

1) Универсальным методом сведения такого типа интегралов к интегралам от рациональных дробей являются так называемая универсальная тригонометрическая подстановка . При этом ,

Выразим и через t

.

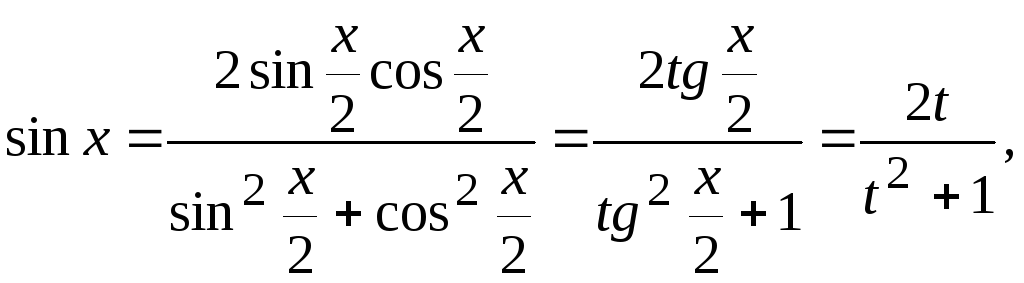
В результате исходный интеграл примет вид:

то есть получили интеграл от рациональной дроби относительно переменной t.

Универсальная подстановка работает всегда. Она, как правило, приводит к громоздким вычислениям, поэтому на практике стараются по возможности использовать более простые приемы.

2) Самая простая ситуация – интегралы вида:

и

Интегралы вида:

3)

Такие интегралы рационализируются подстановкой .

При этом , ,

,

,

.

В результате получим интеграл от рациональной дроби относительно t:

.

4) Интегралы вида где n и m – целые

Такие интегралы находятся по-разному в зависимости от четности n и m или (и) их знаков. Возможны три случая:

а) Хотя бы одно из чисел m и n – нечетное.

Пусть, например, . Тогда

Получили интеграл вида 2), который рационализируется подстановкой . В результате получим интеграл ,

который сводится к табличным.

б) m и n – оба четные и неотрицательные. В этом случае используются формулы понижения степени:

, , .

Пусть . Тогда

В подынтегральном выражении будут присутствовать слагаемые с четными и нечетными степенями .

Слагаемые с нечетными степенями интегрируются как в пункте а), а к слагаемым с четными степенями снова применим формулы понижения степени.

в) m и n – оба четные и среди них есть отрицательное. В этом случае используется подстановка , поскольку это есть частный случай пункта 4).

В интегралах от произведений и используются школьные формулы преобразования произведения в сумму функций.

Пример 34.

.

Пример 35.

.

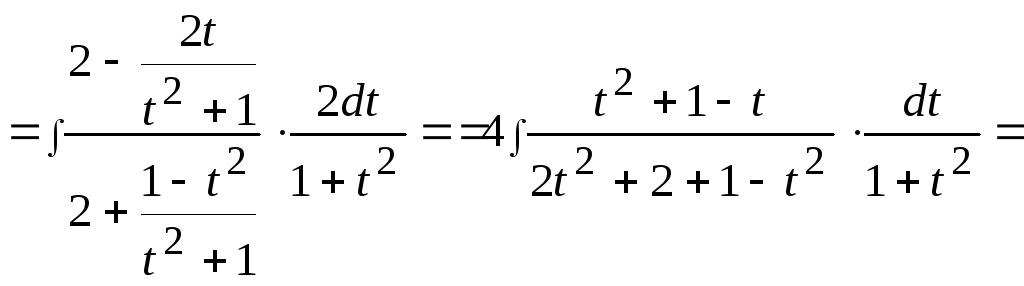
приравниваем коэффициенты при одинаковых степенях:

: __ : __

: с, r:

Тогда получим:

Пример 36.

.

Пример 37.

.

Пример 38.

.

Рекомендуется самостоятельно дорешать пример.

Пример 39.

.

6.1 Вопросы для самопроверки

1. Какая подстановка называется универсальной тригонометрической и почему?

2. Какие тригонометрические формулы используются при интегрировании выражений, содержащих произведение неотрицательных четных степеней 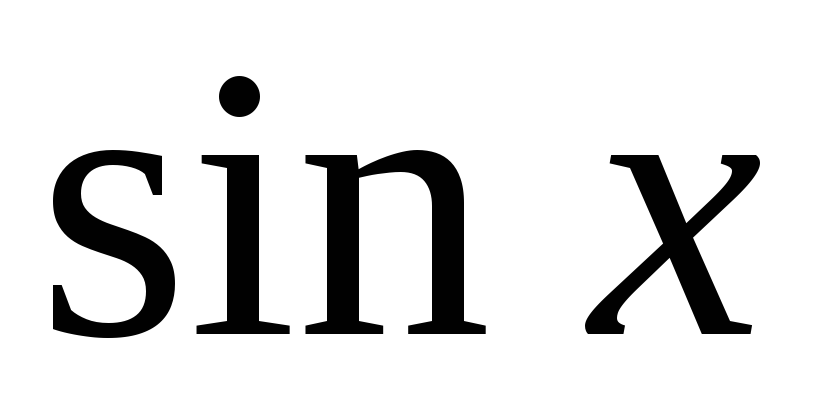и ?

3. Как находятся интегралы в случае, когда в произведении на присутствует нечетная степень?

4. На каких формулах основано вычисление интегралов от функций ;; ?

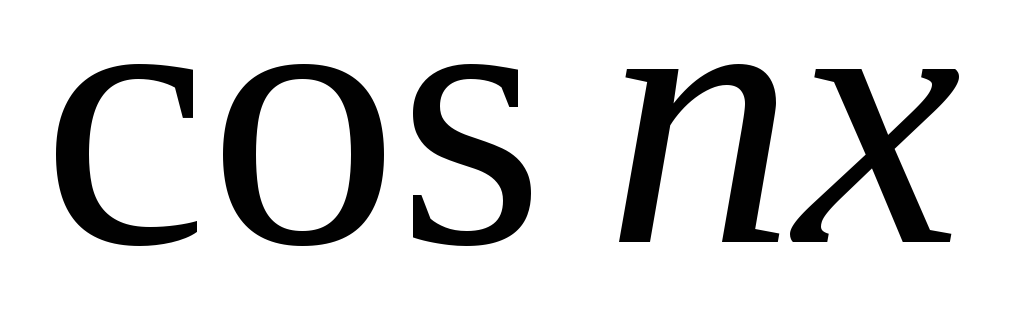5. В каких случаях используется подстановка ?