
- •Введение
- •Способы получения формы изделий
- •Кристаллическое строение металлов
- •Деформация поликристаллических веществ. Влияние омд на структуру и свойства металла
- •Силы и напряжения
- •Деформация
- •Виды деформации. Закон постоянства объема
- •Закон наименьшего сопротивления. Неравномерность деформации
- •Сопротивление деформации
- •Пластичность
Деформация
Лекция
План:
1. Характеристики величины деформации
2. коэффициенты деформации
3. Факторы, влияющие на схему напряженного состояния
О величине деформации судят по изменению размеров деформируемого тела, причем существует несколько вариантов характеристик. Ознакомимся с ними на простейшем примере деформации параллелепипеда. Пусть размеры тела до деформации следующие: длина Lo, ширина bо, толщина ho, а после деформации соответственно L1, b1, h1. Допустим, что в процессе деформации толщина бруса уменьшилась, а длина и ширина увеличились, тогда деформацию можно характеризовать следующими показателями.

Абсолютные деформации:
по толщине — обжатие
![]()
по длине — удлинение
![]()
по ширине — уширение
![]()
Относительные деформации первого вида:
по высоте — относительное обжатие
![]()
по ширине — относительное уширение
![]()
по длине — относительное удлинение
![]()
Относительные деформации второго вида:

Часто относительные деформации выражают в процентах. В этом случае

истинные деформации представляют натуральный логарифм отношения размеров до Деформации и после деформации.
Истинная деформация
по толщине

истинная деформация
по ширине
![]()
истинная деформация
по длине

Истинные деформации представляют уточненную разновидность относительных деформаций.
Коэффициентами деформации называют отношения размеров тела, полученных после деформации к соответствующим размерам до деформации.
Для рассматриваемого случая имеем:
коэффициент деформации по толщине — коэффициент обжатия
![]()
коэффициент деформации по длине — коэффициент удлинения (вытяжка)
![]()
коэффициент деформации по ширине — коэффициент уширения
![]()
Между коэффициентами деформации и соответствующей степенью деформации имеется сравнительно простая связь:

В качестве меры деформации иногда применяют смещенный объем. Смещённым называют объем, удаленный или прибавленный в процессе деформации в одном из направлений.
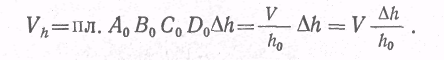
Смещенный объем равен произведению объема деформируемого тела на соответствующую относительную деформацию. В соответствии с этим можно получить:
смещенный объем по длине

и смещенный объем по ширине:

Виды деформации. Закон постоянства объема
Лекция
План:
1. Упругая и остаточная деформация
2. Главные деформации и их схемы.
3. Закон постоянства объема
Под действием внешних сил в деформированном теле первоначально возникают упругие деформации, характеризующиеся упругими отклонениями атомов от положения устойчивого равновесия. Чем больше деформирующая сила, тем больше упругая деформация. Связь между напряжением и упругой деформацией в направлении силы определяется законом Гука:
![]()
где δ—относительная деформация в направлении действия силы;
σ—деформирующие напряжения;
Е— модуль упругости.
В направлении, перпендикулярном действию силы, возникают упругие деформации другого знака. Если в направлении действия силы имеет место деформация растяжения, то в поперечном направлении будет деформация сжатия и, наоборот, если в направлении действия силы возникает деформация сжатия, то в перпендикулярном — деформация растяжения. Поперечная упругая деформация пропорциональна продольной

где δ'—упругая относительная деформация в направлении, перпендикулярном действию силы;
δ— упругая относительная деформация в направлении действия силы;
ν—коэффициент Пуассона — коэффициент пропорциональности продольных и поперечных упругих деформаций.
Величина коэффициента Пуассона зависит от природы деформируемого вещества и характеризует изменение объёма при упругой деформации. Если бы объем металла не изменялся, то коэффициент Пуассона был бы равен 0,5. Фактически в процессе упругой деформации объем металла изменяется и коэффициент Пуассона всегда меньше 0,5, а для стали он равен примерно 0,3.
Главными называют деформации, происходящие в главных направлениях. Подобно схемам главных напряжений, схемы главных деформаций дают графическое представление о наличии или отсутствии деформаций в главных направлениях и их знаке без указания их величины. Всего имеется три возможных схемы главных деформаций.

При наличии схемы D1 уменьшаются размеры по одному главному направлению и увеличиваются по двум другим. При схеме D2 уменьшаются размеры по одному направлению и увеличиваются по другому, по третьему главному направлению деформация отсутствует. При схеме D3 уменьшаются размеры по двум главным направлениям и увеличиваются по третьему.
В одном и том же процессе схема главных напряжений может не совпадать со схемой главных деформаций. Так, например, при схеме главных напряжений, представляющей трехосное сжатие, можно получить все три схемы главных деформаций. Решающую роль при этом играет соотношение величин напряжений, а не их схема. Совокупность схемы главных напряжений и схемы главных деформаций называют механической схемой деформации.
Взаимосвязь между тремя главными деформациями устанавливается на основе условия постоянства объема, согласно которому объем тела при пластической деформации не изменяется.
Если принять, что толщина, ширина и длина параллелепипеда совпадают с главными направлениями, то, исходя из условия постоянства объема, получим

т.е. произведение коэффициентов деформации равно 1. Логарифмируя полученное уравнение, найдем

или
имеем
![]()
Следовательно,
при пластической деформации сумма трех
главных деформаций равна нулю. Представив
выражение в виде
![]()
приходим к выводу, что одна из трех главных деформаций равна сумме двух других и противоположна им по знаку. Эта деформация называется максимальной главной деформацией, по направлению она совпадает с на правлением максимального (по абсолютной величине) - главного напряжения.
Формулу можно представить в виде
 следовательно,
коэффициент вытяжки
следовательно,
коэффициент вытяжки
![]()
