2.2 Определение силовых параметров привода.

Определяем величину вращающих моментов на валах привода:

-на валу двигателя ведущий шкив ременной передачи

M = P_ном/ω₁ (6.4/3/)

M = 4∙10³/75,36 = 53,1 Н∙м

-Ведущий шкив ременной передачи, быстроходный вал редуктора

M₁ = P_ном∙10³∙η₃∙η₂/ ω

M₁ = 4∙10³∙0,97∙0,99/20,93 = 183,5 Н∙м

-Тихоходный вал редуктора

M₂ = P_ном∙10³∙η/ ω3

M₂ = 4∙10³∙0,894/11,63 = 307,5 Н∙м

2.3 Выбор материалов зубчатой передачи

Так как в задание нет особых требований в отношении габаритов передачи, то материал шестерни и колеса выбираем в зависимости от величины вращающего момента на тихоходном валу проектируемого редуктора.

Материал шестерни-сталь 40ХН, улучшение до твердости 350НВ

Материал колеса-сталь 40ХН, улучшение до твердости 320НВ

2.4 Определение допускаемых напряжений

2.4.1 Определение допускаемых контактных напряжений

[σ_н] = σ_но/[S_н]∙K_НL где (9,37/3/)

σ_но - придел контактной выносливости при базовом числе циклов для

выбранного материала (табл. 9,3/3/)

σ_но=2НВ+70

[S_н] - допускаемый коэффициент безопасности

[S_н] = 1,1-при нормализации, улучшении.

K_НL – коэфициент долговечности

K_НL = 1 -при длительной эксплуатации передачи постоянной нагрузке.

Допускаемое контактное напряжение для шестерни.

[σ_н]₁ = 2HB₁+70/[S_н]∙ K_НL

[σ_н]₁ = 2∙350+70/1,1∙1 = 700 Н/мм²

Допускаемое контактное напряжение для колеса.

[σ_н]₂ = 2HB₂+70/[S_н]∙ K_НL

[σ_н]₂ = 2∙320+70/1,1∙1 = 645,5 Н/мм²

Т.к. передача прямозубая то расчет выполняем по допускаемому напряжению

для колеса как менее прочному.

2.4.2 Определяем допускаемое напряжение изгиба

[σ_F] = σ_F0/[S_F]∙K_FL∙F_FC (9/42/3/)

Где σ_F0-придел выносливости зубьев при изгибе (табл.9.3/3/)

σ_F0 = 1.8HВ1

[S_F ] - допускаемый коэффициент безопасности

[S_F] = 1.75-для зубчатых колёс изготовленных из поковок и штамповок

K_FL-коэффициент долговечности K_FL=1.при длительной эксплуатации передачи

K_FC-коэффициент учитывающий влияние двухстороннего приложение нагрузки

K_FC = 1 передача не реверсивная.

Допускаемое напряжение изгиба для шестерни:

σ_F01 = 1,8∙350 = 630 Н/мм²

[σ_F]₁ = σ_F01/ [S_F]∙ K_FL∙K_FC = 308,5 Н/мм²

[σ_F]₁ = 630/1,75 ∙1∙1 = 360 Н/мм²

Допускаемое напряжение для колеса:

σ_F02 = 1,8∙320 = 576 Н/мм²

[σ_F]₂ = σ_F02/ [S_F]∙ K_FL∙ K_FC = 277,7 н/мм²

[σ_F]₂ = 576/1,75∙1∙1 = 329 Н/мм²

Расчет выполняем по допускаемому напряжению изгиба для колеса как

менее прочному.

2.5 Расчёт зубчатой передачи редуктора

2.5.1 Определение межосевого расстояния условия контактной выносливости

рабочих поверхностей зубьев.

(9,26/3/)

Где М₂ - вращающий момент на тихоходном валу редуктора Н∙м

К_HB - коэффициент неравномерности распределение нагрузки по ширине

зубчатого венца

Ψ_а – коэффициент ширины венца колеса относительно межосевого расстояние

принимаем, Ψ_а = 0,5 при симметричном расположении колес.

Значение коэффициента K_HB принимаем в зависимости от делительного

диаметра.

Ψ_d = 0,5Ψа(u_p+1) = 0,5∙ 0,5 (1,8+1) = 0,7 (9.45/3/)

K_HB = 1,03

=138,6∙ = 138,6∙0,777 = 107,69 мм

Значение межосевого расстояние принимаем по ГОСТ 2185-75

а_ω = 107,69 = 125 мм.

2.5.2 Определяем модуль зацепление

m ≥ 6,8 M₂(u_p+1)/u_p a_ω b₂[σ_f2]

где b₂ - это ширина венца зубчатого колеса

b₂ = Ψa∙a_ω

b₂ = 125∙0,5 = 62,5 мм.

принимаем по стандарту из ряда R_a40

b₂ = 63 мм.

m ≥ 6,8∙307,5∙10³ (1,8+1)/1,8∙125∙63∙329 = 1.25 мм принимаем стандартный модуль зацепление по ГОСТ 9563-76

m_n = 1,5 мм.

2.5.3 Определение основных параметров колеса и шестерни

Определяем ширину венца шестерни

b₁ = 1,12 b₂

b₁= 1,12∙63 = 70,56 мм.

Принимаем по стандарту из ряда R_а40

b₁ = 71 мм

Определяем суммарное число зубьев

ƶ_Σ = 2aω/m

ƶ_Σ = 2∙125/1,5 = 166

Определяем число зубьев шестерни и колеса

ƶ₁ = ƶ_Σ(u+1) =166/1,8+1 = 59

ƶ₂ = ƶ_Σ-ƶ = 166-59 = 107

Определяем фактическое передаточное число

u_ф = ƶ₂/ƶ₁

u_ф = 107/59 = 1,8

Что соответствует заданному номинальному значению

Отклонение от заданного значение допускается 4%.

Определяем основные геометрические размеры передачи

Делительный диаметр:

d₁ = mƶ₁ = 1,5∙59 = 89,5 мм

d₂ = mƶ₂ = 1,5∙107 = 160,5 мм

Уточняем межосевое расстояние:

a_ω = (d₁+d₂)/2

a_ω = 89,5+160,5/2 = 125 мм

Окружная скорость зубчатых колёс и степень точности передачи

υ = πn₂d₁/60

υ = 3,14∙200∙89,5/60∙1000 = 0,94 м/с

По табл. 9.1 для у уменьшения динамической нагрузки принимаем 8-ю степень

точности.

2.5.4 Определяем силы в зацепление

Окружная сила:

F_t = 2M₂/d₂ (9.12/3/)

F_t = 2∙307,5/160,5 = 3831,77 H

Радиальная сила:

F_r = F_t∙tgα

F_r = 3831,77∙0,364 = 1394,77 H

Принимаем коэффициент динамической нагрузки

K_hυ = 1,2 (9.6/3/ )

2.5.5 Определяем расчетное контактное напряжение

σ_H = 310/a_ωu_{p (9.25/3/)}

σ_H = 310/125∙1,8 = 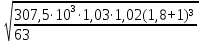= 1,38∙363,913 = 502,2 Н/мм²

Определяем коэффициент формы зуба. Для шестерни и колеса:

Для шестерни: ƶ1 = 59; YF1 = 3,64

Для колеса: ƶ2 = 107; YF2 = 3,6

Сравнительная характеристика зубьев на изгиб для шестерни и колеса.

Для шестерни:

[σ_F]₁/Y_F1 = 360/3,64 = 98,9 H/мм² (9.32/3/)

Для колеса:

[σ_F]₂/Y_F2 = 329/3,6 = 91,4 Н/мм²

Прочность зубьев колеса оказалась ниже прочности зубьев шестерни

[σ_F]₂/Y_F2<[σ_F]₁/Y_F1, поэтому проверочный расчет передачи на изгиб выполняем по зубьям колеса.

Принимаем коэффициенты:

K_FB = 1,06 (9.5/3/)

K_Fυ = 1,4 (9.6/3/)

2.5.6 Определяем расчетное напряжение изгиба в основании ножки зубьев колеса.

σ_F2 = Y_F2 (F_t/b₂m) K_FB K_Fυ < [σ_F]₂ = 329 Н/мм²

σ_F2 = 3,6∙(3831,77/63∙1,5)∙1,06∙1,4 = 217 Н,мм²

Прочность зубьев на изгиб обеспечивается.