Теоретический материал

Импульсом тела называют произведение массы тела на его скорость:

p=mv.

Для системы материальных точек справедливо уравнение

,

где p= – импульс всей системы, F_внешн – равнодействующая всех внешних сил, действующих на нее. Отсюда изменение импульса системы

.

Если геометрическая сумма всех внешних сил равна нулю (например, для замкнутой системы), то dp/dt=0 или p=const – закон сохранения импульса.

Центром масс системы называется воображаемая точка, радиус-вектор которой равен

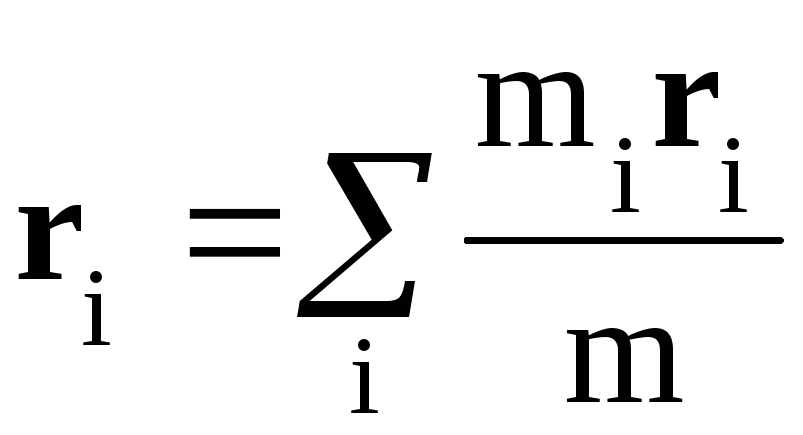
где m=m₁+m₂+….. – общая масса всей системы.

Уравнение движения центра масс системы:

.

Отсюда следует, что центр масс системы движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на систему – теорема о движении центра масс.

Пример решения задачи.

Плот массы M с находящимся на нем человеком массы m неподвижно стоит в пруду. Относительно плота человек совершает перемещение 1^ со скоростью v^(t) и останавливается (рис.3.1). Пренебрегая сопротивлением воды, найти: а) перемещение плота 1 относительно берега; б) горизонтальную составляющую силы, с которой человек действовал на плот в процессе движения.

Дано: M, m, l’, v’(t) _____________ L -? Fч-?

Решение:

Человек и плот образуют замкнутую систему (сумма всех внешних сил, действующих на систему, равна нулю). В замкнутой системе и следовательно, импульс ее сохраняется, т.е. , т.к. плот с человеком сначала покоился. Здесь p_ч и p_n - импульс человека и плота соответственно.

Выберем инерциальную систему отсчета, связанную с берегом, и запишем импульс системы при движении человека по плоту: mv_ч’+Mv=0, где v_ч’- скорость человека относительно берега. v_ч’= v’+v, где v – скорость плота относительно берега, v’- скорость человека относительно плота. Тогда . Зная скорость плота относительно берега, найдем его перемещение: .

Теперь найдем силу, с которой действовал человек на плот: .

Cписок задач

3.1. Система состоит из двух шариков с массами m₁ и m₂, которые соединены между собой невесомой пружинкой. В момент t = 0 шарикам сообщили начальные скорости v₁ и v_2, после чего система начала двигаться в однородном поле тяжести Земли. Пренебрегая сопротивлением воздуха, найти зависимости от времени полного импульса этой системы в процессе движения и радиус - вектора ее центра инерции относительно его начального положения.

Ответ: p = p₀ + mgt, где p₀ = mv₁+ m₂ v₂, m = m₁ + m₂; r₀ = v₀t + gt²/2,

где v₀ = (m₁ v₁+ m₂ v₂)/(m₁+ m₂).

3.2. Две одинаковые тележки 1 и 2, на каждой из которых находится по одному человеку, движутся без трения по инерции навстречу друг другу по параллельным рельсам. Когда тележки поравнялись, с каждой из них на другую перепрыгнул человек - в направлении, перпендикулярном к движению тележек. В результате тележка 1 остановилась, а тележка 2 продолжала двигаться в прежнем направлении так, что ее скорость стала v. Найти первоначальные скорости тележек v₁ и v₂ , если масса каждой тележки (без человека) M, а масса каждого человека m.

Ответ: v₁ = -mv/(M - m), v₂ = Mv/(M - m).

3.3. Две одинаковые тележки движутся друг за другом по инерции (без трения) с одной и той же скоростью v₀. На задней тележке находится человек массы m. В некоторый момент человек прыгнул в переднюю тележку со скоростью u относительно своей тележки. Имея в виду, что масса каждой тележки равна M, найти скорости, с которыми будут двигаться обе тележки после этого.

Ответ: v_задн = v₀ - um/(M + m) ; v_пер = v₀ + umM/(M + m)².

3.4. Цепочка массы m = 1,00 кг и длины l = 1,40 м висит на нити, касаясь поверхности стола своим нижним концом. После пережигания нити цепочка упала на стол. Найти полный импульс, который она передала столу.

Ответ: p = 2m/3=3,5 кг∙м/с.

3.5. Ствол пушки направлен под углом θ = 45⁰ к горизонту. Когда колеса пушки закреплены, скорость снаряда, масса которого в η = 50 раз меньше массы пушки, v₀ = 180 м/c. Найти скорость пушки u сразу после выстрела, если колеса ее освободить.

Ответ: u = v₀cos θ/(1+η) = 25 м/c.

3.6. Пушка массы M начинает свободно скользить вниз по гладкой наклонной плоскости, составляющей угол  с горизонтом. Когда пушка прошла путь l, произвели выстрел, в результате которого снаряд вылетел с импульсом p в горизонтальном направлении, а пушка остановилась. Пренебрегая массой снаряда по сравнению с массой пушки, найти продолжительность выстрела.

Ответ:  = (p соs  - M)/Mg sin .

3.7. Частица 1 столкнулась с частицей 2, в результате чего возникла составная частица. Найти ее скорость v и модуль v, если масса у частицы 2 в  = 2,0 раза больше, чем у частицы 1, а их скорости перед столкновением равны v₁ = 2i + 3j и v₂ = 4i - 5j, где компоненты скорости даны в СИ.

Ответ: v = (v₁+v₂)/(1+); v = 4 м/с.

3.8. На краю покоящейся тележки массы М стоят два человека, масса каждого из которых равна m. Пренебрегая трением, найти скорость тележки после того, как оба человека спрыгнут с одной и той же горизонтальной скоростью u относительно тележки: а)одновременно; б) друг за другом.

Ответ: v₁ = -2mu/(M + 2m); v₂ = -mu(2M + 3m)/(M + m)(M + 2m).

3.9. На носу лодки длиной L стоит человек, держа на высоте h ядро массы m. Масса лодки вместе с человеком равна М. Человек бросает горизонтально ядро вдоль лодки. Какую скорость по горизонтали должен сообщить человек ядру, чтобы попасть в корму лодки? Сопротивление воды движению лодки не учитывать.

Ответ: v = L/(1 + m/M)(2h/g)^1/2 .

3.10. Через блок, укрепленный на потолке комнаты, перекинута нить, на концах которой подвешены тела с массами m₁ и m₂. Массы блока и нитей пренебрежимо малы, трения нет. Найти ускорение центра масс этой системы.

Ответ: a_c = g(m₁- m₂)²/m₁+ m₂)².

4. М Е Х А Н И Ч Е С К А Я Р А Б О Т А И Э Н Е Р Г И Я

Т Е О Р Е Т И Ч Е С К И Й М А Т Е Р И А Л

Элементарной работой силы F на перемещении ds называют скалярное произведение F на ds:

dA = (F ds).

В общем случае, когда материальная точка, двигаясь по криволинейной траектории, проходит путь конечной длины, то работа

.

Работа, отнесенная к единице времени, называется мощностью:

.

Приращение кинетической энергии системы материальных точек равно работе всех сил, действующих на систему:

Е_к2 – Е_к1 = А.

Если работа сил не зависит от пути, а определяется только начальным и конечным положением тела, то такие силы называют консервативными. Работа консервативных сил по любому замкнутому пути равна нулю. Консервативной силой является, например, сила тяжести. Все остальные силы называют неконсервативными. К ним относятся, прежде всего, диссипативные силы, например, сила трения. Работа консервативных сил равна убыли потенциальной энергии системы:

Е_п1 – Е_п2 = А.

В системе с одними только консервативными силами полная механическая энергия остается неизменной. Могут происходить лишь превращения потенциальной энергии в кинетическую и обратно. Это положение называется законом сохранения энергии в механике:

Е_к + Е_п = const.

Если в системе действуют диссипативные силы, то механическая энергия системы уменьшается, переходит, например, во внутреннюю энергию. В этом случае выполняется всеобщий закон сохранения энергии: энергия никогда не создается и не уничтожается, она может только переходить из одной формы в другую.

Связь между силой и потенциальной энергией частицы в поле:

F = -grad E_n.

Примеры решения задач

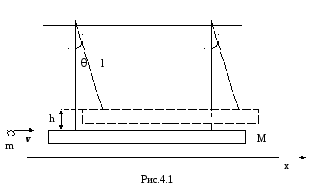
1. Летевшая горизонтально пуля массы m попала, застряв, в тело массы M, которое подвешено на двух одинаковых нитях длины l (см. рис.4.1). В результате нити отклонились на угол θ. Считая m«M, найти: a) скорость пули перед попаданием в тело; б) относительную долю первоначальной кинетической энергии пули, которая перешла в тепло.

Дано:

M, m, m«M, l, θ

_____________

v-? η=Q/E_к-?

Решение:

Импульс пули mv. После того, как пуля застряла в теле, тем же импульсом будет обладать тело вместе с пулей (т.к. удар абсолютно неупругий и выполняется закон сохранения импульса). Т.е. в проекции на ось x: mv = (M+m)v₁ = Mv₁ (т.к. m«M). Отсюда найдем скорость тела после соударения с пулей: v₁ = mv/M. После удара кинетическая энергия тела с пулей будет: . Затем тело начнет подниматься и кинетическая энергия будет превращаться в потенциальную (на тело после удара действует только сила тяжести, она является консервативной). Т.е. . Отсюда найдем скорость пули перед попаданием в тело: .

Во время столкновения в системе действовали диссипативные силы (силы трения), поэтому часть механической энергии перешла в тепловую. Запишем всеобщий закон сохранения энергии в момент удара пули о тело: , где Q – тепловая энергия. Подставив значение v₁, получим: . Тогда .

Ответ: ; .

2. Камень, пущенный по поверхности льда со скоростью v = 3 м/c, прошел до остановки расстояние s = 20,4 м. Найти коэффициент трения k камня о лед.

Дано: v = 3 м/c s = 20,4 м _____________ k-?

Решение:

Работа силы трения при скольжении камня по льду равна (см. рис.4.2):

,

где F_тр = kmg, т.е.

.

Работа силы тяжести и силы реакции опоры равна нулю. С другой стороны, работа равна приращению кинетической энергии камня:

.

Т.к. Е_к2 = 0, то

.

Приравнивая полученные выражения для работы, имеем

.

Подставив численные значения, получим k = 0,02.