0

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Факультет кибернетики

Кафедра Автоматизированных Систем

ОТЧЁТ

к лабораторной работе по дисциплине

«Теория оптимального управления»

«Синтез оптимальных систем с использованием принципа максимума»

^{наименование темы}

Выполнил		АСУ-06-1				Семигузов Е.Ю.
		шифр группы		подпись		Ф.И.О.
Проверил
		должность		подпись		Ф.И.О.

Иркутск 2008 г.

Оглавление:

1. Цель работы. 3

2. Функциональная схема системы управления с данными варианта 3

3. Процесс вычисления ,. 3

4. Графики процесса перехода спутника из заданного положения в нулевое. 6

5. Алгоритм работы системы управления. 6

6. Листинг программы. 7

7. Список литературы. 7

1. Цель работы.

Ознакомление с методикой синтеза оптимальных систем регулирования с использованием средств вычислительной техники.

2. Функциональная схема системы управления с данными варианта

Функциональная схема системы управления представлена на рис. 1.

Момент инерции спутника . Исполнительными органами управления являются реактивные двигатели с регулируемой тягой, развивающие максимальный момент При оптимальном управлении найти время, необходимое для перехода спутника в установившееся нулевое состояние, если в начальный момент времени его отклонение составляло 300°, а угловая скорость -40 градс^-1. Возмущения отсутствуют. Задачу решить, используя принцип максимума Л.С. Понтрягина.

3. Процесс вычисления ,.

Второй закон Ньютона для вращательного движения:

Уравнения движения спутника заданы и при отсутствии возмущений имеют вид

По условию задачи момент должен быть сформирован так, чтобы спутник переходил из любого отклоненного положения в нормально ориентированное за минимальное время.

Поскольку тяга реактивных исполнительных двигателей конечна, то управляющий момент ограничен

Для решения задачи преобразуем уравнение (1), введя обозначения

Тогда уравнение (1) запишется в виде

где нормированная функция управления, модуль которой Сформируем функцию

Для совокупности уравнений (2)

Таким образом, оптимальное по быстродействию управление будет осуществляться в том случае, если регулятор будет переключать исполнительное устройство по релейному закону в соответствии со знаком вспомогательной функции Для того чтобы найти запишем

Интегрируя эти уравнения, получим

где постоянные интегрирования.

Подставив полученные в уравнение (4) получим:

Максимум этой функции с учетом ограничения на управляющий сигнал и обеспечивает оптимальность системы по быстродействию. Очевидно, что при наложенных ограничениях максимум имеет место, если управляющий сигнал формируется исходя из алгоритма

Управляющий сигнал должен менять знак при выходе изображающей точки на линию переключения:

Уравнение линии переключения:

Подставляя числовые значения, получим:

Так как , то

Найдем точку пересечения траектории спутника до переключения и линии переключения.

Уравнение параболы до переключения было - Из этого уравнения необходимо найти , подставив в него начальные условия:

Теперь можно найти точку пересечения этой линии и линии переключения, приравняв оба уравнения:

Подставив в уравнение линии переключения, получим:

Так, как , то .

Найдем время движения до переключения, учитывая, что , получим:

Общее время

4. Графики процесса перехода спутника из заданного положения в нулевое.

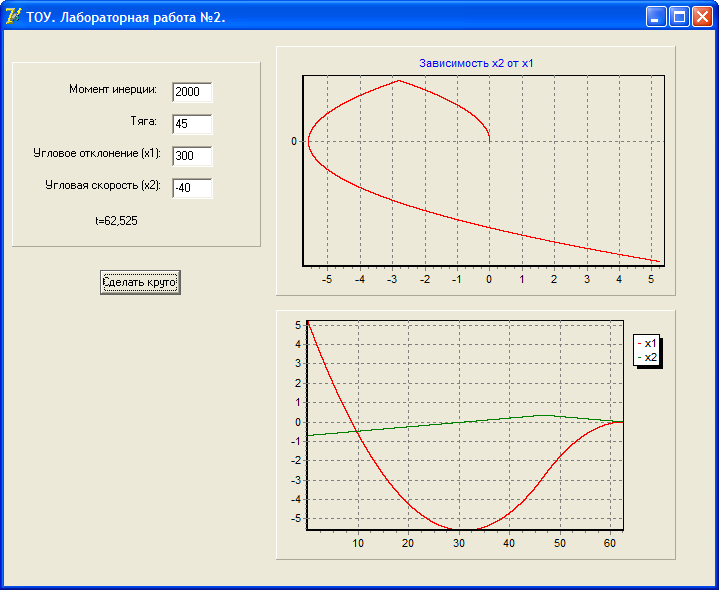
5. Алгоритм работы системы управления.

1) Вычисляем скорость переключения при данном x₁.

2) Устанавливаем значение μ по следующему правилу:

3) Рассчитываем новые значения x_­1 и x_­2 следующим образом:

4) Проверяем, равны ли x_­1 и x_­2 нулю. Если да, то завершение работы алгоритма, иначе возвращаемся к пункту 1.

6. Листинг программы.

var

x1,x2,dt,J,M,k,v_p,Summdt,mu:real;

begin

Series1.Clear;

Series2.Clear;

Series3.Clear;

x1:=StrToFloat(Edit3.Text)*pi/180;

x2:=StrToFloat(Edit4.Text)*pi/180;

J:=StrToFloat(Edit1.Text);

M:=StrToFloat(Edit2.Text);

k:=M/J;

dt:=0.001;

Summdt:=0;

repeat

if x1>=0 then

v_p:=-sqrt(2*k*x1)

else

v_p:=sqrt(abs(2*k*x1));

x2:=x2+dt*k*mu;

if x2<v_p then

mu:=1;

if x2>v_p then

mu:=-1;

if x2=v_p then

begin

if x2<0 then

mu:=1;

if x2>0 then

mu:=-1;

end;

x1:=x1+x2*dt;

Summdt:=Summdt+dt;

Series1.AddXY(x1,x2);

Series2.AddXY(Summdt,x1);

Series3.AddXY(Summdt,x2);

until (abs(x2)<0.001)and(abs(x1)<0.001);

Label5.Caption:='t='+FloatToStr(RoundTo(Summdt,-4));

7. Список литературы.

1. Куцый Н.Н. Теория оптимального управления. Лабораторный практикум: Лабораторные работы № 1,2. – Иркутск, изд-во Иркутск. гос. технич. ун-та, 2001. – 25с.