лабораторная работа / Метод гармонического колебания

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РФ

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

Лабораторная работа №2

Метод гармонического колебания.

Вариант №9.

Выполнил:

студент гр. УИТ-44

Макаров Д.А.

принял:

Скоробогатова Т.Н.

2007 г.

Цель работы: ознакомится с методами гармонической линеаризации нелинейностей и методами расчета параметров автоколебаний в нелинейных системах.

Структурная схема исследуемой системы:

Дано:

К=4, Т1=1, Т2=0.5 d=1

Передаточная функция линейной части:

Зададим нелинейность типа «идеальное реле»:

Примем а=

Проведем анализ системы способом Гольдфарба.

1. На комплексной плоскости построим АФХ линейной части Wл(jw) и зависимость для нелинейной части: -. Для построения последней воспользуемся коэффициентами гармонической линеаризации для нелинейности типа «идеальное реле»:

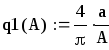
Построим график переходного процесса.

Для получения автоколебаний в системе изменяя коэффициент при старшем члене

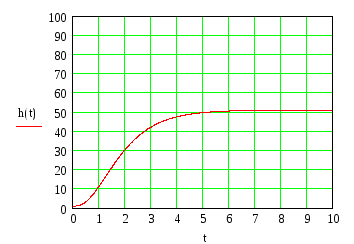
Система не имеет автоколебаний при любом параметре А.

Используя метод гармонического баланса и правила Гольдфарба и Коченбургера, определим устойчивость автоколебаний.

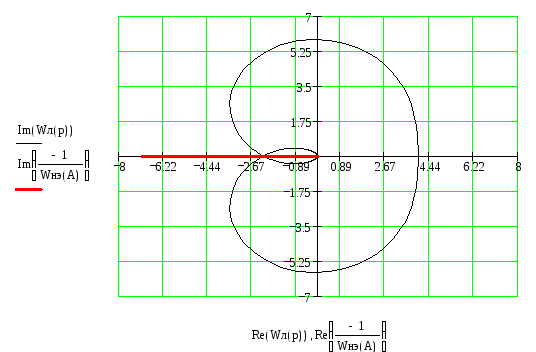
и пересекаются в одной точке , которая соответствует устойчивым автоколебаниям.

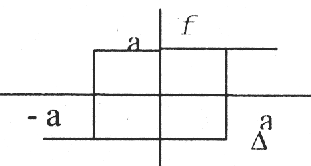
2. Зададим нелинейность типа «реле с гистерезисом»

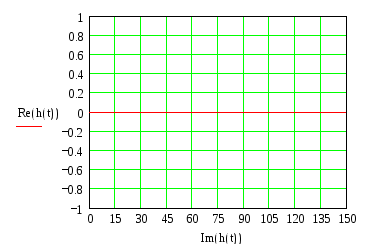
Используя метод гармонического баланса и правила Гольдфарба и Коченбургера,

определим устойчивость автоколебаний.

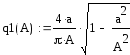
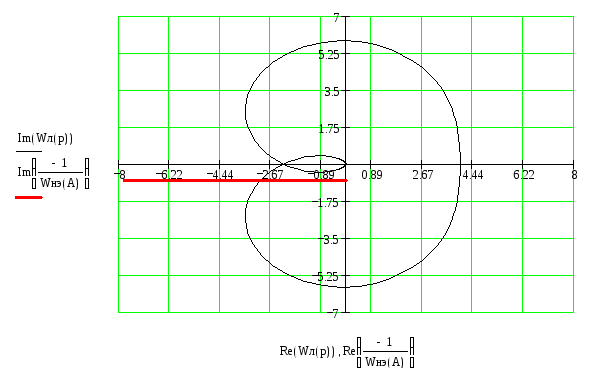
и пересекаются в одной точке .