
лабораторная работа / 1
.docxМинистерство образования и науки Российской Федерации
Балаковский институт техники, технологии и управления
(филиал) ФГБОУ ВПО СГТУ имени Гагарина Ю.А.
Факультет: инженерно-строительный
Кафедра: Управление и информатика в технических системах
Лабораторная работа №1
«ИЗУЧЕНИЕ ГРАФИЧЕСКОЙ ОПЕРАЦИОННОЙ СРЕДЫ СИСТЕМЫ MATLAB”
Выполнила: ст.гр.УИТ-32
Муканалиева Е.Е.
Проверила: Комлева О.А.
Балаково 2012 г.
Цель работы: Изучение графической операционной среды системы MATLAB. Получение навыков работы в системе MATLAB при выполнении вычислительных операций.
Задание 1. Решить систему уравнений. Сформировать матрицу из коэффициентов данной системы уравнений и вектор из свободных членов системы. Для полученного вектора выполнить операции: транспонирование, умножение вектора на число, равное номеру варианта, прибавить к каждому элементу вектору данное число, осуществить поэлементное возведение в степень данного числа полученный вектор. Для матрицы выполнить транспонирование, обращение матрицы, возведение матрицы в степень числа, равного номеру варианта, вычислить матричную экспоненту, выполнить логарифмирование матрицы, вычислить корень.
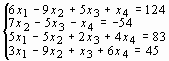
Сформируем из данной системы уравнений матрицу коэффициентов А и матрицу свободных членов В и найдем вектор корней системы уравнений:
>> A=[6,-9,5,1;0,7,-5,-1;5,-5,2,4;3,-9,1,6]
A =
6 -9 5 1
0 7 -5 -1
5 -5 2 4
3 -9 1 6
>> B=[124;-54;83;45]
B =
124
-54
83
45
>> x=A\B
x =
12.0000
1.0000
12.0000
1.0000
Выполним заданные операции с вектором:
>> disp(B')
124 -54 83 45
>> disp(B*15)
1860
-810
1245
675
>> disp(B+15)
139
-39
98
60
>> disp(B.^15)
1.0e+031 *
2.5196
-0.0000
0.0061
0.0000
Выполним заданные операции с матрицей:
>> disp(A')
6 0 5 3
-9 7 -5 -9
5 -5 2 1
1 -1 4 6
>> disp(inv(A))
0.1177 0.1435 0.0935 -0.0581
-0.1468 -0.0694 0.2806 -0.1742
-0.1548 -0.2710 0.3290 -0.2387
-0.2532 -0.1306 0.3194 -0.0258
>> disp(A^15)
1.0e+017 *
2.3906 -6.5918 3.3869 2.2687
-1.3240 3.6508 -1.8758 -1.2565
1.9413 -5.3529 2.7503 1.8423
2.1176 -5.8390 3.0001 2.0097
>> disp(expm(A))
1.0e+006 *
1.8349 -5.0593 2.5995 1.7413
-1.0162 2.8020 -1.4397 -0.9644
1.4900 -4.1084 2.1109 1.4140
1.6253 -4.4816 2.3026 1.5425
>> disp(logm(A))
1.7379 -1.3191 0.3386 0.0280
0.5612 2.2365 -1.4972 0.4066
1.1722 0.3931 0.3019 1.1834
0.9662 -0.7416 -1.0249 2.1534
>> disp(sqrtm(A))
2.3549 -1.7135 0.7767 0.0640
0.3275 2.6890 -1.3972 0.0969
1.2395 -0.3388 1.0390 1.0954
0.8255 -1.4727 -0.4707 2.5701
Задание 3. Вычислить корни полинома, сформировав вектор коэффициентов заданного полинома и вычислить корни с помощью функции roots(p):
>> p=[2 7 8 12];
>> r=(roots(p))
r =
-2.8356
-0.3322 + 1.4162i
-0.3322 - 1.4162i
Для определения коэффициентов полинома воспользуемся функцией poly(r):
>> disp(poly(r))
1.0000 3.5000 4.0000 6.0000
Вычислим значение заданного полинома по значению аргумента, используя функцию polyval:
>> disp(polyval(p,15))
8457
Определим значение коэффициентов производной заданного полинома:
>> disp(polyder(p))
>> disp(polyder(p))
6 14 8
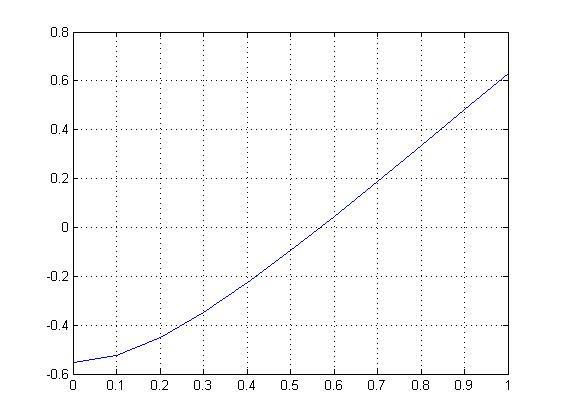
Задание 4. Построить график функции в декартовой и полярной системах координат.
Для построения графика заданной функции зададим диапазон изменения аргумента х, запишем заданную функцию и воспользуемся функцией plot:
>> x=0:0.1:1;
>> y=sqrt(2*x.^2+1.2-cos(x))-1;
>> plot(x,y);grid
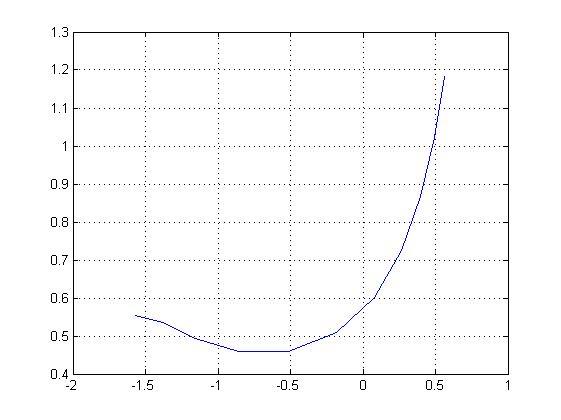
Для построения графика в полярной системе координат необходимо преобразовать декартовые координаты в полярные:
>> x=0:0.1:1;
>> y=sqrt(2*x.^2+1.2-cos(x))-1;
>> [TH,R]=cart2pol(x,y);
>> plot(TH,R),grid
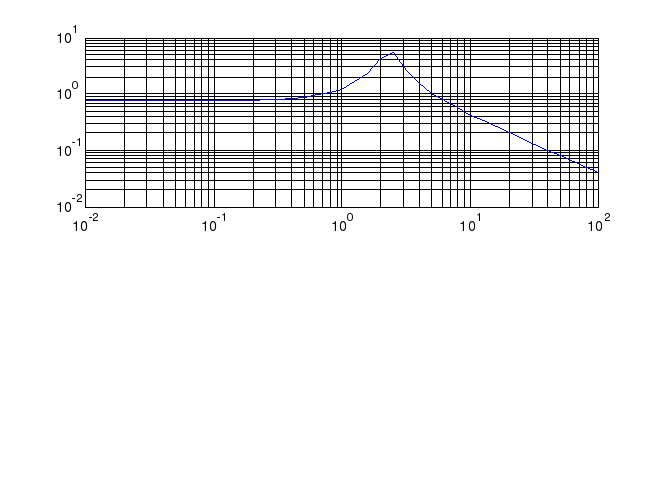
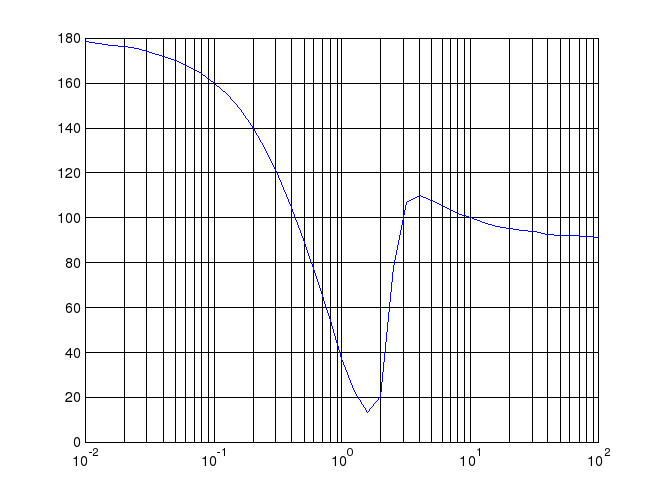
Задание 5. Для построения частотных характеристик воспользуемся последовательностью действий:
>> P1=[-4 7 -3]; P2=[1 0 5 4];
>> roots(P1);
>> roots(P2);
>> om0=1e-2; omk=1e2;
>> OM=logspace(-2,2,41); p=i*OM;
>> ch=polyval(P1,p);zn=polyval(P2,p);
>> ACH=abs(ch)./abs(zn);
>> FCH=angle(ch./zn)*180/pi;
>> subplot(2,1,1);
>> loglog(OM,ACH);grid
>> figure, semilogx(OM,FCH); grid
Амплитудо-частотная характеристика:
Фазово-частотная характеристика:
Вывод: изучила графическую операционную среду системы MATLAB. Получила навыки работы в системе MATLAB при выполнении вычислительных операций.
