лабораторная работа / Лабораторная Т3

Лабораторная работа ТАУ – 3

«Исследование устойчивости динамических режимов

систем автоматического управления»

Выполнил: студент группы

Проверил:

Кострома 2002 год

Цель работы: закрепление теоретических знаний и практических навыков использования критериев устойчивости САУ, экспериментальная проверка теоретических расчетов.

1). Исследование устойчивости системы второго порядка.

Структурная схема имеет вид:

Параметры схемы: To1=0.5, To2=0.5, Co=0.5.

Передаточные функции системы в разомкнутом и замкнутом состоянии:

Теоретически доказать, используя непосредственное решение диффренциального уравнения и трех критериев устойчивости, что при любых значениях варьируемого параметра Сп система будет устойчива.

а). Запишем характеристическое уравнение замкнутой системы:

Найдем корни квадратного уравнения:

Для устойчивости системы необходимо и достаточно, чтобы корни характеристического уравнения имели отрицательную, вещественную часть. Проверим выполнение данного условия при различных значениях Сп.

При Сп=0.1 корни уравнения х1=-1-i, x2=-1+i.

При Сп=0.5 корни уравнения х1=-1-3i, x2=-1+3i.

При Сп=1 корни уравнения х1=-1-4.359i, x2=-1+4.359i.

Видно, что данное условие выполняется, и, следовательно, система является устойчивой.

б). Определение устойчивости по критерию Рауса – Гурвица.

Составим определитель Гурвица из коэффициентов характеристического уравнения.

Для устойчивости системы необходимо и достаточно выполнение условий:

2>0 и 1>0.

1*10*Сп>0 и 1>0, что говорит об устойчивости системы.

в). Определение устойчивости по критерию Михайлова.

Произведем замену в характеристическом уравнении p на jw:

По данному выражению построим годограф Михайлова.

Годограф, построенный по данному выражению, при изменении частоты от 0 до , начинаясь на действительной полуоси, огибает против часовой стрелки начало координат, пройдя последовательно 2 квадранта. То есть система является устойчивой.

г). Определение устойчивости по критерию Найквиста.

Запишем передаточную функцию разомкнутой системы:

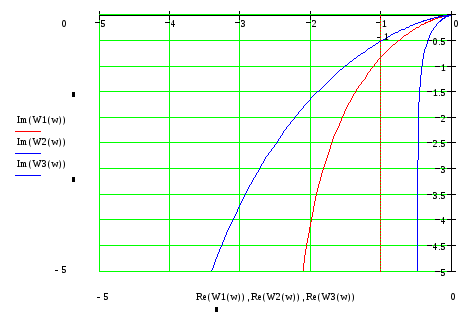
По данному выражению построим

годограф Найквиста.

Разомкнутая система устойчива,

так как при любом значении Сп

годограф не охватывает точку

(-1; j0).

Теоретические экспериментальные кривые:

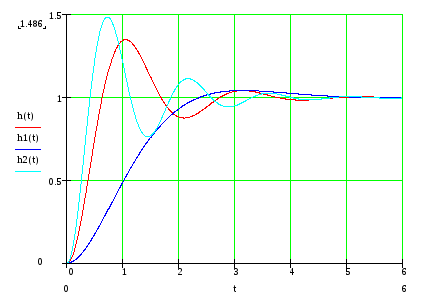
Были получены экспериментальные кривые:

2). Исследование замкнутой системы, находящейся на грани устойчивости.

Структурная схема системы.

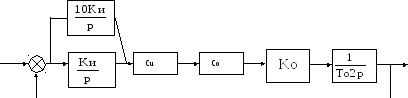
Параметры схемы: To1=0, To2=0.5, Co=0.25.

Передаточные функции системы в разомкнутом и замкнутом состояниях:

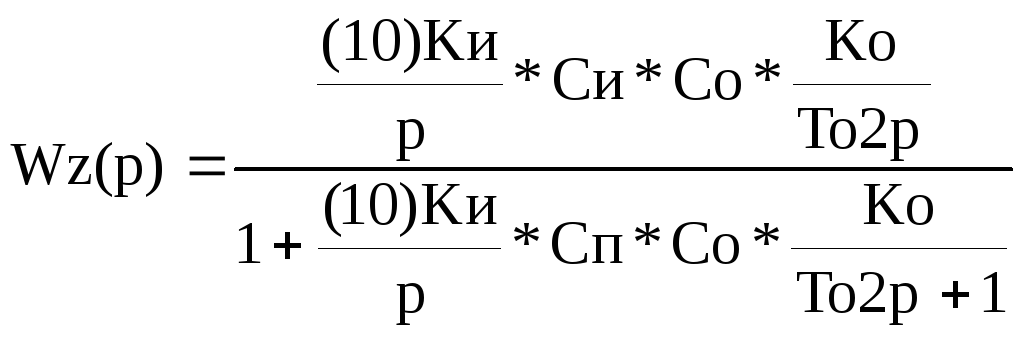
Теоретически доказать, используя непосредственное решение диффренциального уравнения и трех критериев устойчивости, что при любых значениях варьируемого параметра Сп система будет находиться на грани устойчивости.

а). Непосредственное решение дифференциального уравнения.

Запишем характеристическое уравнение замкнутой системы:

Найдем корни квадратного уравнения:

Для нахождения системы на границе устойчивости необходимо и достаточно, чтобы корни характеристического уравнения были чисто мнимыми. Проверим выполнение данного условия при различных значениях Си и Ки.

При Си=0.1, Ки=1 корни уравнения х1=0.224i, x2=-0.224i.

При Си=0.5, Ки=10 корни уравнения х1=1.581i, x2=-1.581i.

При Си=1, Ки=1 корни уравнения х1=0.707i, x2=-0.707i.

Видно, что данное условие выполняется, и, следовательно, система находится на границе устойчивости.

б). Определение устойчивости по критерию Рауса – Гурвица.

Составим определитель Гурвица из коэффициентов характеристического уравнения.

Для нахождения системы на границе устойчивости необходимо и достаточно выполнение условий:

2=0 и 1=0.

Видно, что при любых Си и Ки главный определитель и диагональные миноры равны нулю, то есть условие выполняется при любых значениях параметров системы.

в). Определение устойчивости по критерию Михайлова.

Произведем замену в характеристическом уравнении p на jw:

По данному выражению построим годограф Михайлова.

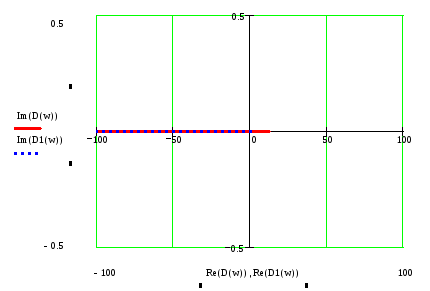
Годограф, построенный по данному выражению, при изменении частоты от 0 до , начинаясь на действительной полуоси, проходит через начало координат, идет по вещественной оси. То есть система находится на грани устойчивости при любых Си и Ки.

г). Определение устойчивости по критерию Найквиста.

Запишем передаточную функцию разомкнутой системы:

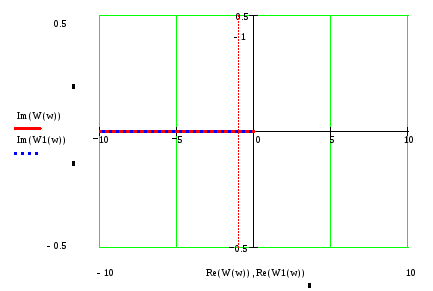
По данному выражению построим

годограф Найквиста.

Разомкнутая система находится на,

грани устойчивости, так как при любом

значении Си и Ки годограф Найквиста

проходит через точку (-1; j0).

Теоретические экспериментальные кривые:

Были получены экспериментальные кривые:

Экспериментальные данные подтверждают нахождение системы на границе устойчивости.

3). Исследование устойчивости замкнутой системы третьего порядка.

Структурная схема системы:

Параметры схемы:

To1=0.5, To2=0.5, Co=1.

Передаточные функции системы в разомкнутом и замкнутом состояниях.

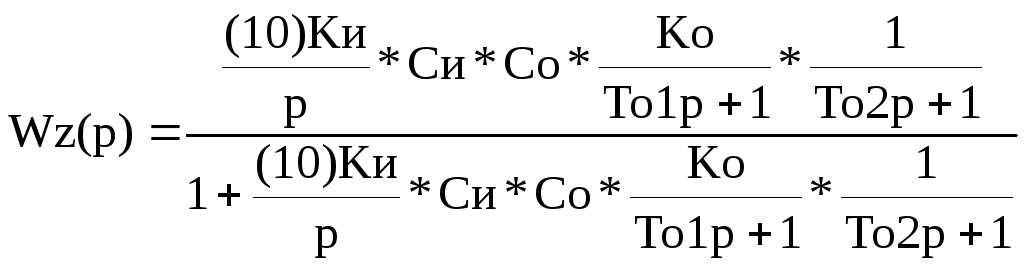
С помощью критерия Рауса – Гурвица определить критическое значение результирующего коэффициента Kкр=Kи*Си.

Запишем характеристическое уравнение системы:

Для данного характеристического уравнения составим определитель Гурвица и его диагональные миноры:

To1*To2>0 10*Ku*Cu>0

(To1+To2)>0 (To1+T02)-To1*To2*10*Ku*Cu>0

То есть можно записать:

(To1+T02)> To1*To2*10*Ku*Cu

(1)

Подставим исходные данные и определим значение коэфициента Kкр:

Kкр=0.4.

Определим теоретически устойчивость системы при различных значениях Kкр:

• при Ku*Cu=1.2Kкр неравенство (1) не выполняется и система будет неустойчивой.

• при Ku*CuKкр неравенство (1) выполняется и система будет находится на границе устойчивости.

• при Ku*Cu=0.3Kкр и Ku*Cu=0.5Kкр неравенство (1) выполняется и система будет устойчивой.

Построим кривые переходного процесса, соответствующие данным случаям:

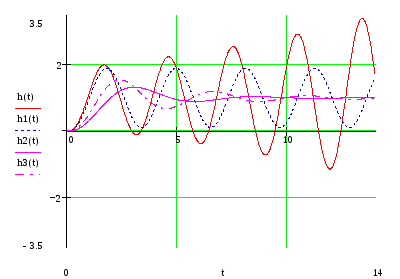
Были получены следующие экспериментальные переходные процессы:

Вывод: полученные переходные характеристики подтверждают теоретические расчеты об устойчивости системы с помощью критерия Рауса – Гурвица. Изменение какого-либо параметра системы или их совокупности может в корне изменить устойчивость системы. В данном случае критическое сочетание параметров системы: Ku*Cu=0.4.

4). Исследование структурно неустойчивой замкнутой системы.

Структурная схема системы.

Параметры схемы: To1=0.5, To2=1, Co=0.5.

Передаточные функции разомкнутой и замкнутой систем:

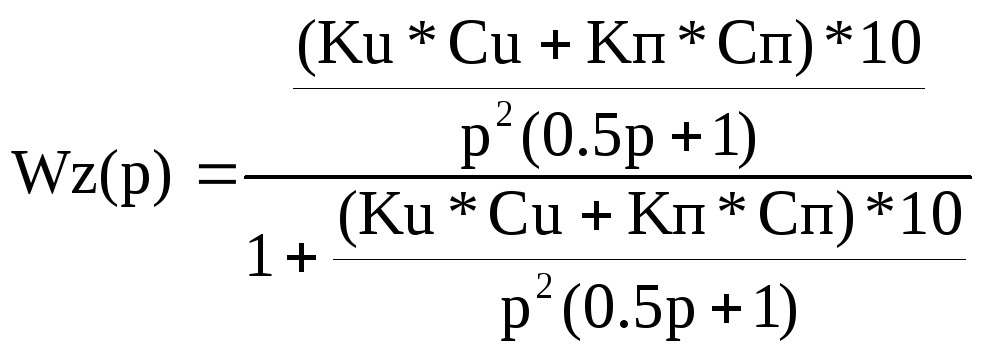
Теоретически доказать, что Кп*Сп=0 система будет структурно неустойчивой при любых параметрах системы.

Запишем характеристическое уравнение замкнутой системы:

Составим определитель Гурвица из коэффициентов характеристического уравнения и дигональные миноры:

To2>0

10*Kп*Сп>0

To2*0-10*Kп*Cп*To1*To2>0

То есть при любых параметрах системы Kп и Cп система будет структурно неустойчивой.

С помощью одного из критериев устойчивости определить критическое значение коэффициента П–регулятора Kпкр=Kп*Си, при добротности П – регулятора Kи*Си=1 и Kи*Си=0.5.

Воспользуемся критерием устойчивости Рауса – Гурвица.

Запишем характеристическое уравнение:

To2>0

10*Kп*Сп>0

To2*0-10*(Kп*Cп+Ku*Cu)*To1*To2>0 (1)

Критическое значение определится, как: Kпкр=To1*To2=0.5.

Аналогично при Kи*Си=0.5 Kпкр=0.25.

• при Kп*Сп=0.8Kпкр неравенство (1) не выполняется, система будет неустойчивой.

• при Kп*Сп=Kпкр система находится на границе устойчивости.

• при Kп*Сп=1.2Kпкр и Kп*Сп=2Kпкр неравенство (1) выполняется, система будет устойчивой.

Экспериментально полученные графики.

Вывод: Экспериментальные результаты подтверждают теоретические данные, касающиеся того, что при СпКп=0 система является структурно неустойчивой при любых параметрах системы. Но в то же время систему можно сделать устойчивой путем введения в ее структуру П-регулятора с определенными параметрами. То есть структурно неустойчивую систему можно сделать устойчивой только путем изменения ее структуры, но не изменением соотношения параметров звеньев, ее составляющих.

12