Тема 9. №1. Вычислить пределы: а) ; б) ; в) ; г) ; д) ; е) .

Тема 10. №1. Найти асимптоты кривой у = 2х + arctg x. №2. Найти интервалы монотонности функции у = . №3. Найти экстремумы функции у = х ²(1 - х). №4. Найти интервалы выпуклости и точки перегиба кривой у = . №5. Построить графики функций: а) у = ; б) у = 2х - 3; в) у = (х – 1) е ^{1 – х}; г) у = .

Тема 11. №1. Найти область определения функции z = и изобразить её графически. №2. Найти частные производные функции и = tg. №3. Вычислить приближённое значение 3,01 ^2,03 с помощью дифференциала. №4. Найти производную функции и = arccos в точке М₀ (1; 1; 1) по направлению вектора l = {2; 1; 2}. №5. Найти градиент функции z = в точке М₀(0; 3) и его модуль.

Тема 12. №1. Найти наибольшее и наименьшее значения функции у = 3 - 6 + 4х – 8 на отрезке [- 1; 8]. №2. Из прямоугольного листа картона размером 2,4 × 1,5 м ² требуется изготовить коробку без крышки. Какова должна быть сторона квадратов, вырезанных из четырёх углов листа, чтобы объём полученной коробки был максимальным? Чему равен объём такой коробки? №3. Окно в загородном доме имеет форму прямоугольника, завершённого полукругом. Периметр окна равен Р. При каком радиусе полукруга площадь окна будет наибольшей?

№4. Найти экстремумы функций: а) z = х ² + у ² + ху – 4х – 5у; б) z = - х – 2у.

№5. Найти наименьшее и наибольшее значения функции z = ln (х + у) в области (х – 2)² + (у – 2)² ≤ 1. №6. Найти условные экстремумы функции z = при х + у = 2. №7. Общие издержки производства заданы функцией С = 0,5х ² + 0,6ху + 0,4у ² + 700х + + 600у + 2000, где х и у – количества товаров А и В. Общее количество произведён-ной продукции должно быть равно 500 ед. Сколько единиц товара А и В нужно про- изводить, чтобы издержки на их изготовление были минимальными? Тема 13. №1. 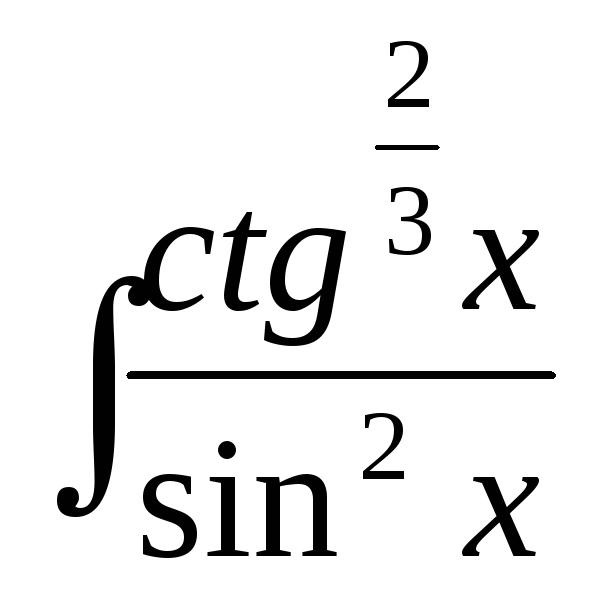Найти интегралы: а) ; б) ; в) ; г) dx; д) dx; е) ; ё) dx; ж) dx; з) dx; и) dx; й) dx; к) dx; л) dx; м) dx; н) dx; о) ; п) ; р) ; с) cos ⁵dx; т) dx; у) cos 4x dx; ф) dx; х) ; ц) ; ч) ; ш) dx; щ) .

Тема 14. №1. Вычислить интегралы: а) dx; б) ; в) .

Тема 15. №1. Вычислить интегралы или установить их расходимость: а) ; б) X dx.

Тема 16. №1. Вычислить площади фигур, ограниченных линиями: а) у = х ² + 4х, у = х + 4; б) у = х sin x, у = 0, 0 ≤ х ≤ π. №2. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограни- ченной линиями у = 4х – х ², у = х. №3. Вычислить объём тела, образованного вращением вокруг оси Оу фигуры, ограни- ченной линиями у = х, х = - 4, у = 0.

Тема 17. №1. Решить уравнения и, где указано начальное условие, найти частный интеграл: а) dx = xy dy; б) (1 + е ^х) уу’ = е ^х, у (0) = 1; в) у ² + х ²у’ = хуу’; г) (х ² – 3у ²) dx + 2xy dy = 0, у (2) = 1; д) у = х (у’ – х cos x); е) ху’ + у – е ^х = 0, у (а) = b; ж) у’ + 2у = у²е ^х; з) (3х ²у – 4ху ²) dx + (x ³ – 4x ²y + 12y ³) dy = 0.

Тема 18. №1. Решить задачи Коши и построить найденные интегральные кривые: а) у’’’ = , у (1) = 2, у’ (1) = 1, у’’ (1) = 1; б) у’’ = , у (1) = , у’ (1) = 1; в) у ³у’’ = 1, у = 1, у’ = 1.

Тема 19. №1. Найти общие решения уравнений: а) у’’’ – 8у = 0; б) у ⁽⁴⁾ – у = 0; в) у ⁽⁵⁾ – 6у ⁽⁴⁾ + 9у’’’ = 0; г) у ⁽⁴⁾ - 5у’’ + 4у = 0; д) у’’ + 4у’ + 4у = хе ^2х; е) у ⁽⁴⁾ + 5у’’ + 4у = 3 sin x.