
- •Рабочая программа модуля
- •080100.62 «Экономика»
- •1. Цели освоения дисциплины.
- •2. Место дисциплины в структуре ооп.
- •3. Требования к результатам освоения дисциплины.
- •4. Структура и содержание модуля.
- •1. Функции.
- •2. Пределы.
- •6. Интеграл.
- •5. Образовательные технологии.
- •Тема 1. Трансцендентное исчисление. А) Логарифмы.
- •Тема 3. Функции и их графики.
- •Тема 9. Вычисление пределов с помощью производной. №1. Вычислить пределы: а) ; б) ; в) ; г) ; д) ; е) ; ё) ; ж) ; з) .
- •Тема 13. Неопределённый интеграл. А) Непосредственное интегрирование. №1. Найти интегралы: а) ; б) ; в) ; г) .
- •Тема 14. Определённый интеграл. №1. Вычислить интегралы: а) dx; б) ; в) dx.
- •Тема 15. Несобственные интегралы. №1. Вычислить интегралы или установить их расходимость: а) ; б) ; в) ; г) ln X dx.
- •Тема 20. Числовые ряды. А) Знакоположительные ряды. №1. Исследовать ряды на сходимость: а) ; б) ; в) ; г) ; д) ; е) ; ё) ; ж) ; з) .
- •Тема 21. Степенные ряды. №1. Определить области сходимости степенных рядов: а) ; б) ; в) ; г) ; д) .
- •Тема 2.
- •Тема 9. №1. Вычислить пределы: а) ; б) ; в) ; г) ; д) ; е) .
- •Тема 14. №1. Вычислить интегралы: а) dx; б) ; в) .
- •Тема 15. №1. Вычислить интегралы или установить их расходимость: а) ; б) X dx.
- •Тема 20. №1. Исследовать ряды на сходимость: а) ; б) ; в) ; г) ; д) ; е) ; ё) ; ж) ; з) .
- •Тема 21. №1. Найти области сходимости степенных рядов: а) ; б) ; в) .
- •7. Учебно-методическое и информационное обеспечение модуля.
- •8. Материально-техническое обеспечение модуля.
Тема 20. Числовые ряды. А) Знакоположительные ряды. №1. Исследовать ряды на сходимость: а) ; б) ; в) ; г) ; д) ; е) ; ё) ; ж) ; з) .
б) Знакопеременные ряды.
№2.
Исследовать ряды на абсолютную и
условную сходимости:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
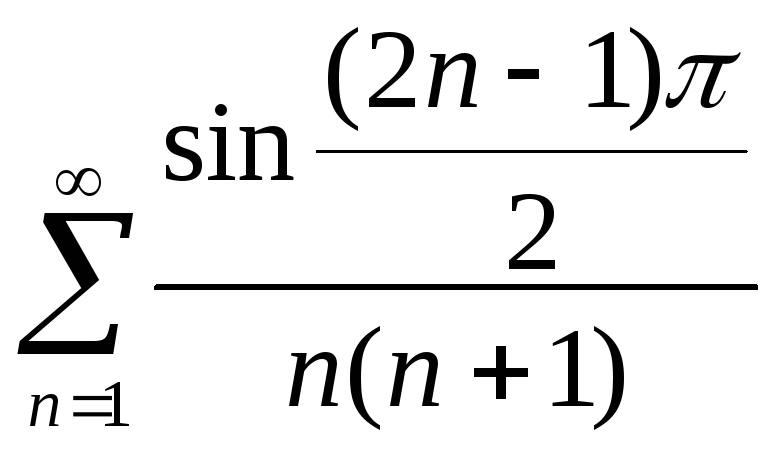 .
.
Тема 21. Степенные ряды. №1. Определить области сходимости степенных рядов: а) ; б) ; в) ; г) ; д) .
Тема 22. Ряды Тейлора и
Маклорена.
а) Разложение функций
в ряд Тейлора.
№1. Разложить функцию
у =
![]() в ряд Тейлора по степеням (х +
2).
б) Разложение функций в ряды
Маклорена с помощью основных
разложений.
№2. Разложить функции
в ряды Маклорена: а)
в ряд Тейлора по степеням (х +
2).
б) Разложение функций в ряды
Маклорена с помощью основных
разложений.
№2. Разложить функции
в ряды Маклорена: а)
![]() ;
б) cos 2x;
в)
;
б) cos 2x;
в)
![]() ;
г)
;
г)
![]() .
в) Почленное интегрирование и
дифференцирование рядов.
№3.
Разложить функцию
.
в) Почленное интегрирование и
дифференцирование рядов.
№3.
Разложить функцию
![]() в ряд по степеням х и почленным
интегрированием
данного ряда написать
ряд для функции arcsin
x.
№4. Применяя
почленное дифференцирование, вычислить
сумму ряда
в ряд по степеням х и почленным
интегрированием
данного ряда написать
ряд для функции arcsin
x.
№4. Применяя
почленное дифференцирование, вычислить
сумму ряда
![]() .
.
г) Приближённые вычисления с помощью рядов.
№5. Вычислить приближённо sin
1 и оценить погрешность вычисления.
№6. Вычислить cos 10
с точностью до 10 – 6.
№7.
Пользуясь тождеством
![]() = arcsin
= arcsin![]() ,
найти число π с точностью до 10 –
4.
,
найти число π с точностью до 10 –
4.
Домашние задания:
Тема 1.
№1. Вычислить: а) 16![]() ;
б) lg│cos
π│
;
б) lg│cos
π│![]() + log 4 1.
+ log 4 1.
№2. Что больше: log 3
4 или log 0,5 7?
№3.
Определить знак числа
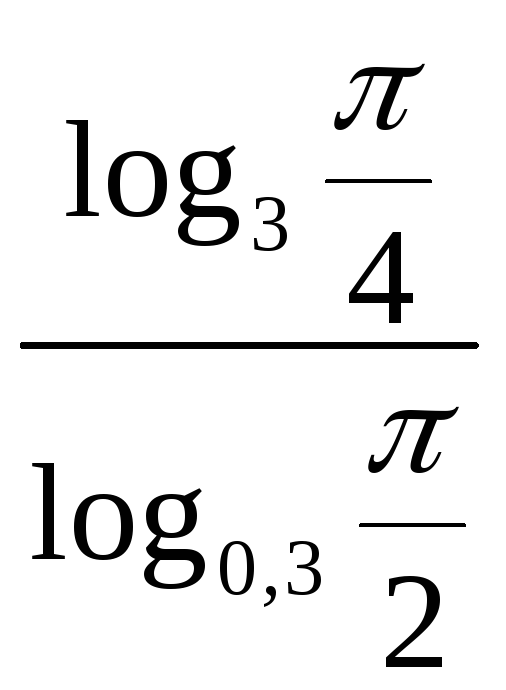 .
№4.
Найти область определения функции у
= lg
.
№4.
Найти область определения функции у
= lg
![]() .
№5.
Дано: ctg
.
№5.
Дано: ctg![]() = -
= -
![]() ,
6300 <
,
6300 <
![]() < 7200. Найти остальные функции
этого угла.
№6. Упростить:
а)
< 7200. Найти остальные функции
этого угла.
№6. Упростить:
а)
![]() ;
б)
;
б)
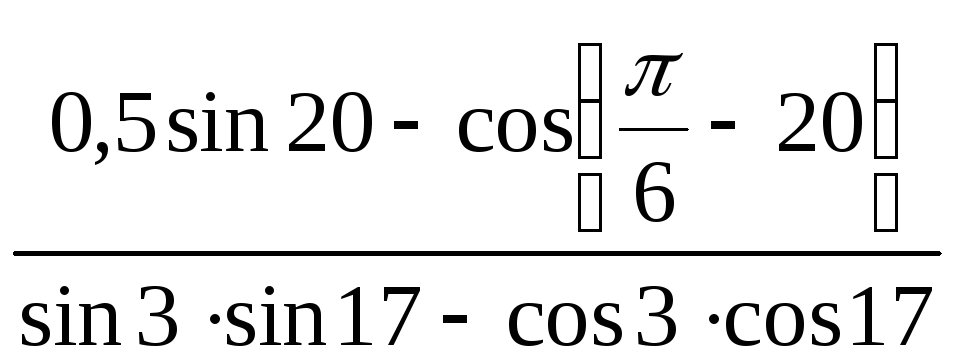 ;
в) cos
;
в) cos![]() ;
г)
8 cos
;
г)
8 cos
![]() cos
cos
![]() cos
cos
![]() ;
д) sin
;
д) sin![]() .
№7.
Дано: tg
.
№7.
Дано: tg![]() + ctg
+ ctg
![]() = 3. Найти sec2
= 3. Найти sec2![]() + cosec2
+ cosec2![]() .
.
№8. Дано: cos![]() =
=
![]() ,
,
![]() <
<
![]() < 2π. Найти tg 2
< 2π. Найти tg 2![]() .
.
Тема 2.
№1. Вычислить:
а)
![]() ;
б)
;
б)
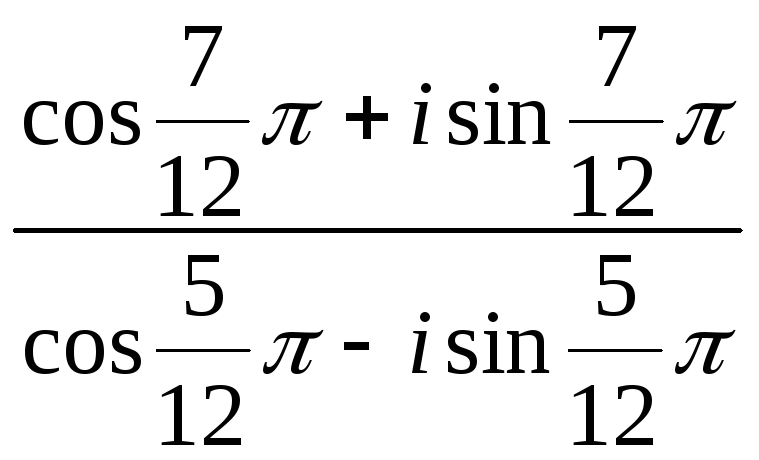 ;
в) (1 + i
;
в) (1 + i![]() )(1
+ i)
)(1
+ i)![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() .
№2.
Решить уравнения:
а) х 2 + 4 =
0; б) х 2 – 6х + 18 = 0; в) х
4 – 30х 2 + 289 = 0.
.
№2.
Решить уравнения:
а) х 2 + 4 =
0; б) х 2 – 6х + 18 = 0; в) х
4 – 30х 2 + 289 = 0.
Тема 3.
№1. Найти области
определения функций:
а) f
(x) =
![]() +
+
![]() ;
б) f (x)
=
;
б) f (x)
=
![]() ;
в)
;
в)
![]() (3
+ 5х – 2х 2).
№2. Найти
множества значений функций:
а) f
(x) = 5 + 4х – х 2;
б) f (x)
=
(3
+ 5х – 2х 2).
№2. Найти
множества значений функций:
а) f
(x) = 5 + 4х – х 2;
б) f (x)
=
![]() .
№3.
Построить графики функций:
а) у
= |х 2 - 5|х| + 6| - 2; б) у
= 2| log2 |х - 1||.
.
№3.
Построить графики функций:
а) у
= |х 2 - 5|х| + 6| - 2; б) у
= 2| log2 |х - 1||.
Тема 4.
№1. Построить кривые:
а)
х 2 + 2у 2 – 4х + 4у
+ 2 = 0; б) у 2 + 6у + 2х
+ 5 = 0;
в) х 2 + у 2 + 10х
- 4у + 13 = 0; г) 9х 2 – 16у
2 + 90х + 32у – 367 = 0.
№2. Составить
уравнение окружности, проходящей
через точки пересечения окружнос-
ти
х 2 + у 2 + 4х – 4у
= 0 с прямой у = - х и точку М1(4;
4).
№3. Написать каноническое уравнение
симметричного относительно осей
координат
эллипса, который проходит
через точку М(5/4; 1) и имеет эксцентриситет
ε = 3/5.
№4. Дан эллипс
![]() = 1. Составить уравнение гиперболы,
вершины которой нахо-
дятся в фокусах,
а фокусы в вершинах данного эллипса.
№5.
Составить каноническое уравнение
параболы, если её фокус находится в
точке
пересечения прямой 4х – 3у
– 4 = 0 с осью Ох.
= 1. Составить уравнение гиперболы,
вершины которой нахо-
дятся в фокусах,
а фокусы в вершинах данного эллипса.
№5.
Составить каноническое уравнение
параболы, если её фокус находится в
точке
пересечения прямой 4х – 3у
– 4 = 0 с осью Ох.
Тема 5.
№1. Доказать, что
![]() .
Определить, начиная с какого номера
члены данной последовательности
будут отличаться от её предела на
величину, меньшую 0,1; 0,01; 0,001.
№2. Доказать,
что
.
Определить, начиная с какого номера
члены данной последовательности
будут отличаться от её предела на
величину, меньшую 0,1; 0,01; 0,001.
№2. Доказать,
что
![]() = - 2. Определить, на какую величину
= - 2. Определить, на какую величину
![]() должен отличаться аргумент х от
- 1, чтобы данная функция отличалась
от своего предела на величину, меньшую
чем 0,1; 0,03.
должен отличаться аргумент х от
- 1, чтобы данная функция отличалась
от своего предела на величину, меньшую
чем 0,1; 0,03.
№3. Доказать, что
![]() не существует.
№4. Вычислить: а)
не существует.
№4. Вычислить: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
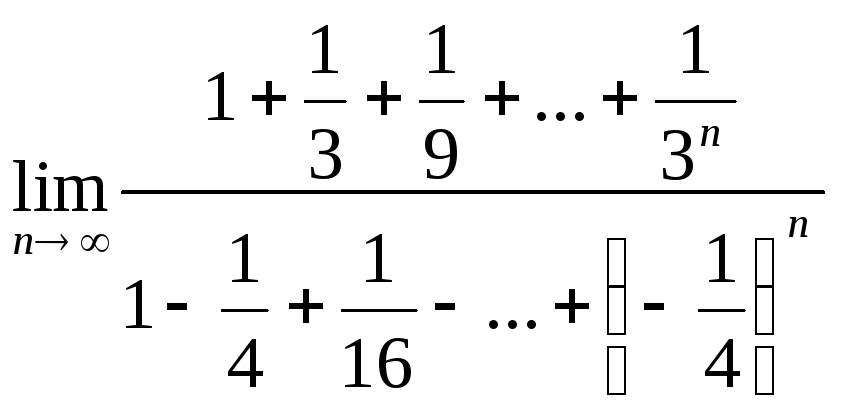 ;
е*)
;
е*)
![]() ;
ё)
;
ё)
![]() ;
ж)
;
ж)
![]() ;
з*)
;
з*)![]() ;
и)
;
и)
![]() ;
й)
;
й)
![]() ;
к)
;
к)
![]() ;
л)
;
л)
![]() ;
м)
;
м)
![]() ;
н)
;
н)
![]() ;
о)
;
о)
![]() ;
п)
;
п)
![]() ;
р)
;
р)
![]() ;
с)
;
с)
![]() ;
т)
;
т)
![]() ;
у)
;
у)
![]() .
.
Тема 6.
№1. Исследовать на
непрерывность функции:
а) у =
![]() ;
б) у =
;
б) у =
![]() ;
в) у =
;
в) у =
![]() .
.
Тема 7.
№1. Используя
определение, найти производные
функций:
а) у = tg
![]() ;
б) у = 3х.
№2. Найти
производные функций:
а) у =
;
б) у = 3х.
№2. Найти
производные функций:
а) у =
![]() ;
б) у =
;
б) у =
![]() ;
в) у = ln (3x
2 +
;
в) у = ln (3x
2 +
![]() );
г) у =
);
г) у =
![]() + ln sinx;
д)
у = ln arctg
+ ln sinx;
д)
у = ln arctg
![]() ;
е) у = х arctg
x.
№3. Найти
производную у’x
, если arcsin y
= x 2y
3 – 7yx 2.
;
е) у = х arctg
x.
№3. Найти
производную у’x
, если arcsin y
= x 2y
3 – 7yx 2.
№4. Найти производные п-го порядка:
а) у = cos x;
б) у = 2 х + 2 – х;
в) у =
![]() .
.
Тема 8.
№1. Найти дифференциал
функции у =
![]() .
№2.
Найти приближённые значения: а)
(1,015)5; б) tg 460.
.
№2.
Найти приближённые значения: а)
(1,015)5; б) tg 460.
