
- •Рабочая программа модуля
- •080100.62 «Экономика»
- •1. Цели освоения дисциплины.
- •2. Место дисциплины в структуре ооп.
- •3. Требования к результатам освоения дисциплины.
- •4. Структура и содержание модуля.
- •1. Функции.
- •2. Пределы.
- •6. Интеграл.
- •5. Образовательные технологии.
- •Тема 1. Трансцендентное исчисление. А) Логарифмы.
- •Тема 3. Функции и их графики.
- •Тема 9. Вычисление пределов с помощью производной. №1. Вычислить пределы: а) ; б) ; в) ; г) ; д) ; е) ; ё) ; ж) ; з) .
- •Тема 13. Неопределённый интеграл. А) Непосредственное интегрирование. №1. Найти интегралы: а) ; б) ; в) ; г) .
- •Тема 14. Определённый интеграл. №1. Вычислить интегралы: а) dx; б) ; в) dx.
- •Тема 15. Несобственные интегралы. №1. Вычислить интегралы или установить их расходимость: а) ; б) ; в) ; г) ln X dx.
- •Тема 20. Числовые ряды. А) Знакоположительные ряды. №1. Исследовать ряды на сходимость: а) ; б) ; в) ; г) ; д) ; е) ; ё) ; ж) ; з) .
- •Тема 21. Степенные ряды. №1. Определить области сходимости степенных рядов: а) ; б) ; в) ; г) ; д) .
- •Тема 2.
- •Тема 9. №1. Вычислить пределы: а) ; б) ; в) ; г) ; д) ; е) .
- •Тема 14. №1. Вычислить интегралы: а) dx; б) ; в) .
- •Тема 15. №1. Вычислить интегралы или установить их расходимость: а) ; б) X dx.
- •Тема 20. №1. Исследовать ряды на сходимость: а) ; б) ; в) ; г) ; д) ; е) ; ё) ; ж) ; з) .
- •Тема 21. №1. Найти области сходимости степенных рядов: а) ; б) ; в) .
- •7. Учебно-методическое и информационное обеспечение модуля.
- •8. Материально-техническое обеспечение модуля.
Тема 1. Трансцендентное исчисление. А) Логарифмы.
№1. Вычислить:
а) log
12 3 + log 12 4; б)
log![]() 45
– log
45
– log![]() 3;
в) log 64 128; г)
100
3;
в) log 64 128; г)
100![]() ;
д) 49
;
д) 49![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
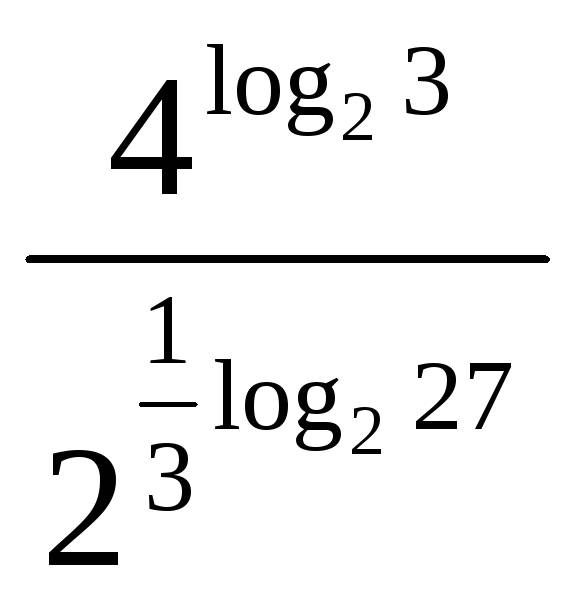 .
.
№2. Вычислить log 5 9,8, если lg 2 = a, lg 7 = b.
№3. Доказать неравенство: log 4 6 > log 6 4.
№4. Определить знаки чисел: а) log
1,7
![]() ;
б) log 0,3
;
б) log 0,3![]() .
.
№5. Найти область определения функции
у = lg![]() .
б)
Тригонометрические преобразования.
№6.
Найти наибольшее и наименьшее значения
выражения 2 – sin
.
б)
Тригонометрические преобразования.
№6.
Найти наибольшее и наименьшее значения
выражения 2 – sin
![]() .
№7.
Дано: cos
.
№7.
Дано: cos![]() = -
= -
![]() ,
π <
,
π <
![]() <
<
![]() .
Найти остальные функции числа
.
Найти остальные функции числа
![]() .
№8.
Упростить:
а)
.
№8.
Упростить:
а)
![]() ;
б) sin 4
;
б) sin 4![]() + cos 4
+ cos 4![]() + sin 2
+ sin 2![]() cos 2
cos 2![]() ;
в)
;
в)
![]() ;
г)
tg (π -
;
г)
tg (π -
![]() )
)![]() + sin (2π -
+ sin (2π -
![]() )
cos
)
cos![]() - cos 2(π
-
- cos 2(π
-
![]() );
д) cos 200 – sin
200
);
д) cos 200 – sin
200![]() 100.
100.
№9. Выразить через tg
![]() выражение sin 4
выражение sin 4![]() - cos 4
- cos 4![]() .
№10.
Дано: tg
.
№10.
Дано: tg
![]() + ctg
+ ctg
![]() = 3. Найти tg 3
= 3. Найти tg 3![]() + ctg3
+ ctg3
![]() .
№11.
Дано: ctg 2
.
№11.
Дано: ctg 2![]() =
=
![]() ,
0 <
,
0 <
![]() <
<
![]() .
Найти cos
2
.
Найти cos
2![]() .
№12.
Дано: cos (3π - 4
.
№12.
Дано: cos (3π - 4![]() )
=
)
=
![]() .
Найти 27 cos
4 2
.
Найти 27 cos
4 2![]() .
№13.
Дано: sin
.
№13.
Дано: sin
![]() =
=
![]() .
Найти 4 tg
2
.
Найти 4 tg
2![]() .
№14.
Дано: sin
.
№14.
Дано: sin
![]() =
=
![]() .
Найти 16 sin
4
.
Найти 16 sin
4![]() .
№15.
Дано: ctg
.
№15.
Дано: ctg
![]() = 3. Найти sin
= 3. Найти sin
![]() .
№16.
Дано: cos 2
.
№16.
Дано: cos 2![]() =
=
![]() .
Найти 9
.
Найти 9![]() .
.
№17. Дано:
![]() = 2arcctg (- 2) -
= 2arcctg (- 2) -
![]() .
Найти sin 3
.
Найти sin 3![]() .
№18.
Вычислить tg (arcsin
(- 0,8)).
№19. Построить на единичной
окружности arccos
.
№18.
Вычислить tg (arcsin
(- 0,8)).
№19. Построить на единичной
окружности arccos
![]() .
№20.
Что больше: arccos
.
№20.
Что больше: arccos
![]() или arcctg
или arcctg
![]() ?
?
Тема 2. Комплексные числа.
№1.
Выполнить действия:
а) (2 + 3i)
+ (4 – 7i); б) (1 – i)(3
+ 2i); в)
![]() .
№2.
Заданы ли следующие комплексные числа
в тригонометрической форме:
а) 2
.
№2.
Заданы ли следующие комплексные числа
в тригонометрической форме:
а) 2![]() ;
б) - 3
;
б) - 3![]() ;
в) 5
;
в) 5![]() ;
г) 4
;
г) 4![]() .
№3.
Записать комплексное число - 3 – 4i
в тригонометрической форме.
№4.
Вычислить, используя тригонометрическую
форму числа:
а)
.
№3.
Записать комплексное число - 3 – 4i
в тригонометрической форме.
№4.
Вычислить, используя тригонометрическую
форму числа:
а)
![]() ;
б) (1 + i
;
б) (1 + i![]() )
– 5; в)
)
– 5; в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
№5.
Решить уравнения:
а) х 2 + 1 =
0; б) х 2 – 2х + 10 = 0; в) х
4 – 6х 2 + 25 = 0.
.
№5.
Решить уравнения:
а) х 2 + 1 =
0; б) х 2 – 2х + 10 = 0; в) х
4 – 6х 2 + 25 = 0.
Тема 3. Функции и их графики.
а) Свойства функций.
№1. Найти
области определения функций:
а) f
(x) =
![]() ;
б) f (x)
=
;
б) f (x)
=
![]() ;
в) f (x)
=
;
в) f (x)
=
![]() + 3arccos
+ 3arccos![]() ;
г)
f (x)
= log 2(2 – x)
+ 2log x5;
д) f (x)
= log 0,5 log
3 x.
;
г)
f (x)
= log 2(2 – x)
+ 2log x5;
д) f (x)
= log 0,5 log
3 x.
№2. Найти множества значений функций:
а) f (x)
= |х + 1| - 3; б) f
(x) =
![]() ;
в) f (x)
=
;
в) f (x)
=
![]() .
.
б) Преобразование графиков.
№3.
Построить графики функций:
а) у = -
2
![]() ;
б) у = х 2 - 5|х| + 6; в) у =
|2(х – 1)2 - 4|х - 1| - 16| + 3; г) у
=
;
б) у = х 2 - 5|х| + 6; в) у =
|2(х – 1)2 - 4|х - 1| - 16| + 3; г) у
=
![]() .
.
Тема 4. Кривые 2-го порядка. а) Задачи на построение кривых. №1. Построить кривые: а) 16х 2 – 9у 2 – 64х + 54у – 161 = 0; б) х 2 + у 2 – 8х + 6у – 11 = 0; в) у 2 – 8у – 4х = 0; г) х 2 + 4у 2 – 6х + 8у – 3 = 0.
б) Задачи на составление уравнений.
№2.
Составить уравнение окружности,
проходящей через точки М1(1; 2),
М2(0; - 1),
М3(- 3; 0).
№3. Составить
каноническое уравнение эллипса,
проходящего через точки М1![]() ,
М2
,
М2![]() .
№4.
Написать каноническое уравнение
гиперболы, симметричной относительно
осей координат, если она проходит
через точку М1(
.
№4.
Написать каноническое уравнение
гиперболы, симметричной относительно
осей координат, если она проходит
через точку М1(![]() ;
;
![]() ),
а эксцентриситет равен
),
а эксцентриситет равен
![]() .
№5.
Написать уравнение параболы, если она
проходит через точки пересечения
пря-
мой х + у = 0 и окружности
х 2 + у 2 + 4у = 0 и
симметрична относительно оси Оу.
№6.
Составить уравнение окружности,
проходящей через точки М1(7; 7),
М2(- 2; 4), если её центр лежит на
прямой 2х – у – 2 = 0.
№7*. Написать
уравнение эллипса, если расстояние
между фокусами равно расстоя-нию
между концами большой и малой осей.
№8.
Составить уравнение гиперболы, если
её асимптоты заданы уравнениями у
= ±
.
№5.
Написать уравнение параболы, если она
проходит через точки пересечения
пря-
мой х + у = 0 и окружности
х 2 + у 2 + 4у = 0 и
симметрична относительно оси Оу.
№6.
Составить уравнение окружности,
проходящей через точки М1(7; 7),
М2(- 2; 4), если её центр лежит на
прямой 2х – у – 2 = 0.
№7*. Написать
уравнение эллипса, если расстояние
между фокусами равно расстоя-нию
между концами большой и малой осей.
№8.
Составить уравнение гиперболы, если
её асимптоты заданы уравнениями у
= ±
![]() х
и
гипербола проходит через точку М(10;
- 3
х
и
гипербола проходит через точку М(10;
- 3![]() ).
).
Тема 5. Пределы.
а)
Определения пределов.
№1. Доказать,
что
![]() .
Определить, начиная с какого номера
члены данной последовательности
будут отличаться от её предела на
величину, меньшую
ε = 0,1; 0,01; 0,001.
№2.
Доказать, что
.
Определить, начиная с какого номера
члены данной последовательности
будут отличаться от её предела на
величину, меньшую
ε = 0,1; 0,01; 0,001.
№2.
Доказать, что
![]() = - 1. Определить, на какую величину
= - 1. Определить, на какую величину
![]() должен отличаться аргумент х от
- 1, чтобы данная функция отличалась
от своего предела на величину, меньшую
чем ε = 0,1; 0,02.
должен отличаться аргумент х от
- 1, чтобы данная функция отличалась
от своего предела на величину, меньшую
чем ε = 0,1; 0,02.
№3. Доказать, что
![]() не существует.
не существует.
б) Алгебраические приёмы раскрытия
неопределённостей.
№4. Вычислить:
а)
![]() ; б)
; б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() (2х
5 – 10х 3 – 1); ё)
(2х
5 – 10х 3 – 1); ё)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
и)
;
и)
![]() ;
й)
;
й)
![]() ;
к)
;
к)
![]() ;
л)
;
л)
![]() ;
м)
;
м)
![]() ;
н)
;
н)
![]() ;
о)
;
о)
![]() ;
п)
;
п)
![]() ;
р)
;
р)
![]() ;
с)
;
с)
![]() .
в)
Замечательные пределы.
№5. Вычислить:
а)
.
в)
Замечательные пределы.
№5. Вычислить:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
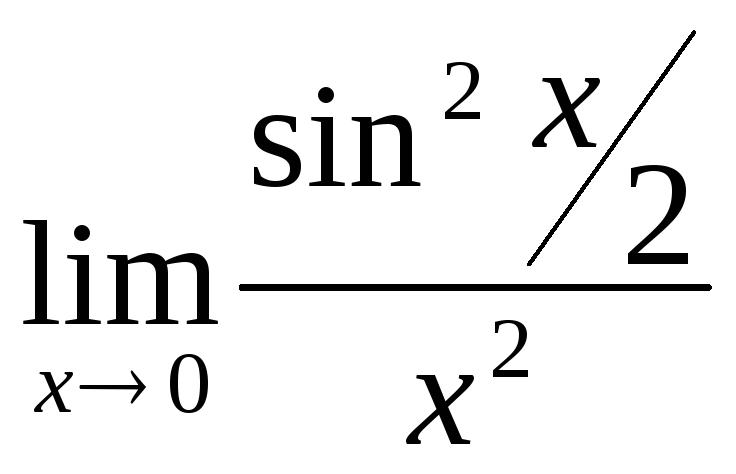 ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
ё)
;
ё)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
и)
;
и)
![]() ;
й)
;
й)
![]() ;
к)
;
к)
![]() .
.
г) Вычисление пределов с помощью
эквивалентностей.
№6. Вычислить:
![]() .
.
Тема 6. Непрерывность
функции.
№1. Исследовать на
непрерывность функции:
а) у =
![]() ;
б) у = 3 -
;
б) у = 3 -
![]() ;
в) у =
;
в) у =
![]() ;
г) у =
;
г) у =
![]() ;
д*) у =
;
д*) у =
![]() .
.
Тема 7. Производная функции.
а)
Вычисление производных с помощью
определения.
№1. Используя определение,
найти производные функций:
а) у
=
![]() ;
б) у = cos 2x;
в) у =
;
б) у = cos 2x;
в) у =
![]() .
.
б) Практикум по вычислению
производных.
№2. Найти производные
функций:
а) у = 2х 7 – 5х
2 + 2![]() + 1; б) у =
+ 1; б) у =
![]() +
+
![]() ;
в) у =
;
в) у =
![]() ln x; г)
у =
ln x; г)
у =
![]() - arctg x;
д)
у =
- arctg x;
д)
у =
![]() ;
е) у = sin
;
е) у = sin![]() ;
ё) у =
;
ё) у =
![]() arcsin
arcsin![]() +
+
![]() ;
ж) у = ln (х +
;
ж) у = ln (х +
![]() );
з)
у = ln
);
з)
у = ln![]() ;
и) у =
;
и) у =
![]() ;
й) у =
;
й) у =
![]() ;
к) у =
;
к) у =
![]() .
.
в) Производная неявной функции. №3. Найти производную у’x , если ух + log 2(х 2 + у 2) – sin (ху) = 0.
г) Производные высших порядков.
№4.
Найти производную у’’’, если у
= 5х 4 -
![]() + 2 х.
№5. Найти производные
п-го порядка: а) у = sin
x; б) у = ln
x.
+ 2 х.
№5. Найти производные
п-го порядка: а) у = sin
x; б) у = ln
x.
Тема 8. Дифференциал.
№1.
Найти полное приращение функции у
= 2х 3 + 3х 2 + 6х и
её дифференциал, сравнить их.
№2.
Найти приближённые значения: а) arctg
0,97; б)
![]() .
.
