4.4 Критерий Михайлова

Для использования критерия требуется в характеристическом уравнении использовать преобразование p=jω. Используем данное преобразование:

D(jω)=0.692102782ω⁴-j6.6918393ω³-18.428238ω²+j14.27276397ω+1.001183313=0

Кроме того: D(jω)=X(ω)+jY(ω), тогда

X(ω)=0.692102782ω⁴-18.428238ω²+1.001183313

Y(ω)=-6.6918393ω³+14.27276397ω

Графики оформлены в MathCAD, с постепенным увеличением масштаба.

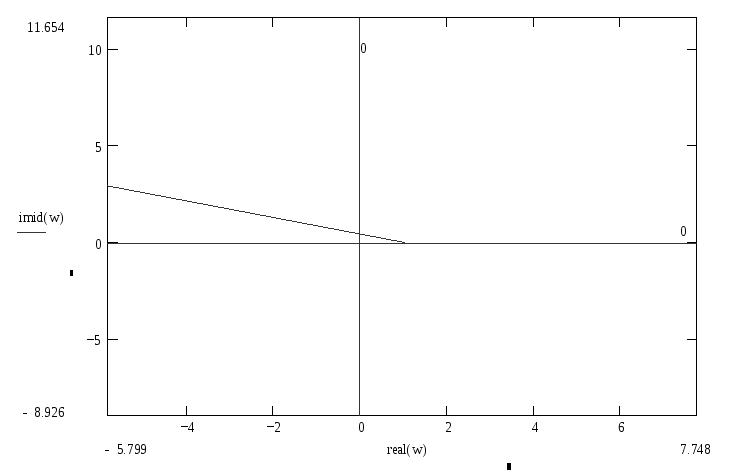
Рисунок 1, а

Р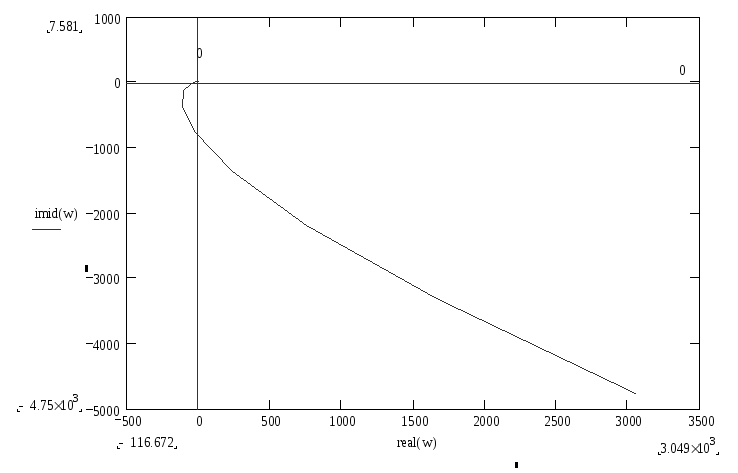исунок 1, б

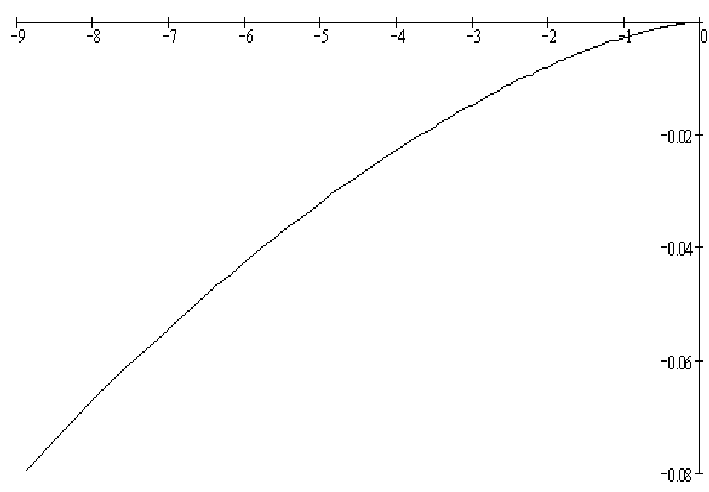
Рисунок 1, в

Последний график показывает, что условие K=π/2*n, где K-угол поворота годографа, n-порядок характеристического уравнения, соблюдено. График уходит в бесконечность в 4 квадранте, система устойчива.

4.5 Критерий Найквиста

Требуется представить передаточную функцию в комплексной форме.

Соберем коэффициенты и выделим реальную и мнимую части.

а) б)

Рисунок 2

Согласно критерию Найквиста система устойчива, т.к. график не охватывает (-1; 0) и заканчивается на положительной полуоси.

4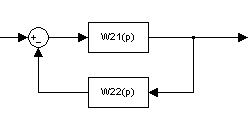.6 D-разбиение

Схема 8

Введем ООС с коэффициентом передачи W₂₂(p)=1 и примем W₉(p)=k , тогда

Характеристическое уравнение примет вид:

Используем замену p=jω, тогда:

Выделим реальную и мнимую части:

Re(k(ω))=

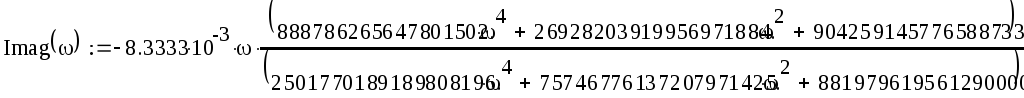
Im(k(ω))=

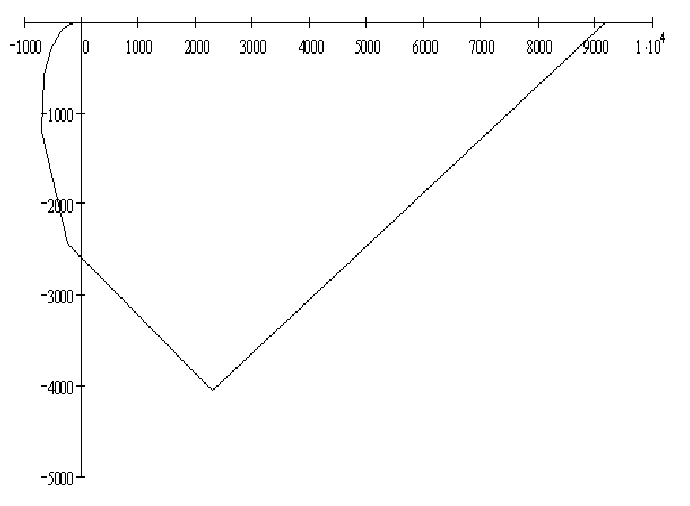
Рисунок 3

Согласно графику область k>-1.09E-4, является областью подозрительной на устойчивость. Определим правильность предположения с помощью критерия Гурвица. Примем k=5, то характеристическое уравнение запишется в виде:

=1.009E+12

(6.6918393)= 6.6918393

=1.345E+4

=3.579E+8

Т.о. система устойчива в области k>-1.09E-4

4.7 Критерий Ляпунова

Для того чтобы САУ была устойчива необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части.

Из передаточной функции замкнутой системы определим характеристическое уравнение.

Ниже приведено решение характеристического уравнения при помощи MathCAD.

Как видно, все корни отрицательные, т.е. система устойчива.

ВЫВОД

В ходе расчетно-графической работы мне была предоставлена СУ, имеющая некоторые недоработки. Я смог исправить недостатки и получить устойчивую систему, последнее было доказано с использованием семи критериев. Однако стоит отметить два критерия, которые являются наиболее простыми в своих классах: критерий Гурвица и Михайлова. Как показало построение АФЧХ, запас устойчивости не велик. Однако учитывая состав звеньев в системе (преобладание апериодических звеньев), данная ситуация трудно исправима и требует введение дополнительных звеньев, что не предусмотрено данной расчетной работой. Стоит отметить, что цель работы, получить устойчивую систему и проверить ее устойчивость, выполнена.

13