6.2. Общий вид уравнения кривой второго порядка. Упрощение уравнения с помощью преобразования системы координат

Кривой второго порядка называется линия, которая в декартовой системе координат имеет уравнение второй степени относительно координат х и y.

Общее уравнение второй степени относительно переменных х и у может содержать члены второй степени , первой степе­ни (х, y) и нулевой степени (свободный член). Оно имеет вид

,

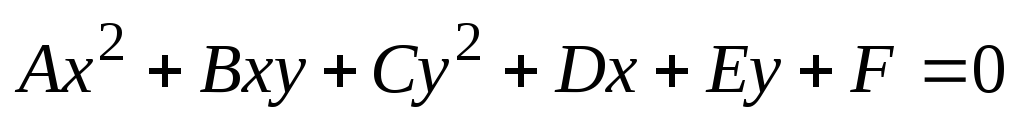(6.3)

где А, В, С, D, Е, F – действительные числа, причем хотя бы один из коэффициентов А, В, С отличен от нуля.

Пример 6.3. В уравнении коэффициенты при переменных соответственно равны , ,, , , .

Исследуем уравнение (6.3). Пусть . Можно так повернуть систему координат, чтобы в уравнении исчез член с произведением координат.

Воспользуемся формулами (6.2) поворота данной системы на угол , получим

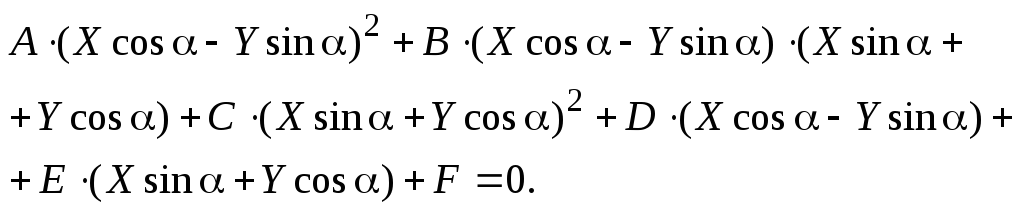
Раскрыв скобки и приведя подобные члены, полу­чим уравнение второй степени относительно переменных X и Y. Член с произведением координат X и Y имеет следующий вид:

.

Учитывая, что

получаем

.

Выберем угол поворота так, чтобы выполнялось равенство

Из условия следует, что . Разделив обе части равенства на получаем

,

или

,

(6.4)

Используя (6.4), можно выбрать угол так, чтобы после поворота координатных осей на этот угол в уравнении линии второго порядка не осталось члена с произведением координат. Тогда уравнение примет вид

,

(6.5)

Если в уравнение второй степени входит квадрат неизвестного, то с помощью параллельного переноса мож­но освободиться от первой степени этого неизвестного. Пусть урав­нение (6.5) содержит квадрат неизвестного , т.е. .

Рассмотрим члены, содержащие х.

.

Выражение в скобках дополним до полного квадрата

.

Тогда уравнение (6.5) примет вид

.

Осуществим параллельный перенос системы координат хОу

, .

Новое начало координат О′ имеет координаты , в системе хОy. Аналогично избавляемся от члена с первой степени переменной y.

В системе XO′Y уравнение рассматриваемой линии примет вид

.

Если в уравнении второй степени коэффициент при квадра­те переменной y равен нулю, то уравнение имеет вид

.

В этом случае переходим к системе коорди­нат, в которой уравнение линии не содержит первой степени х, т.е.

.

Если в уравнении второй степени коэффициент при квадра­те переменной х равен нулю, то уравнение имеет вид

.

В этом случае переходим к системе коорди­нат, в которой уравнение линии не содержит первой степени у, т.е.

.

6.3. Иcследование уравнения линии второго порядка

Линии вто­рого порядка делятся на три типа:

1. эллиптический. К нему относятся линии с уравнениями

,

где , и числа А и В имеют одинаковые знаки.

2. гиперболический. К нему относятся линии с уравне­ниями

,

где , и числа А и В имеют разные знаки.

3. параболический. К нему относятся линии с уравнениями

,

где , и

,

где .

Рассмотрим уравнение эллиптического типа. Если коэффициент , то обе части уравнения можно разделить на С. Тогда урав­нение примет вид

,

или

.

Будем считать, что числа А и В положительны, в противном случае, умножим обе части урав­нения на –1. Рассмотрим следующие случаи:

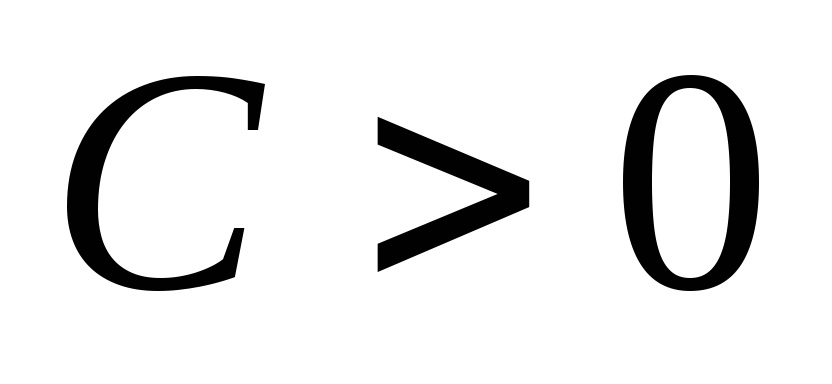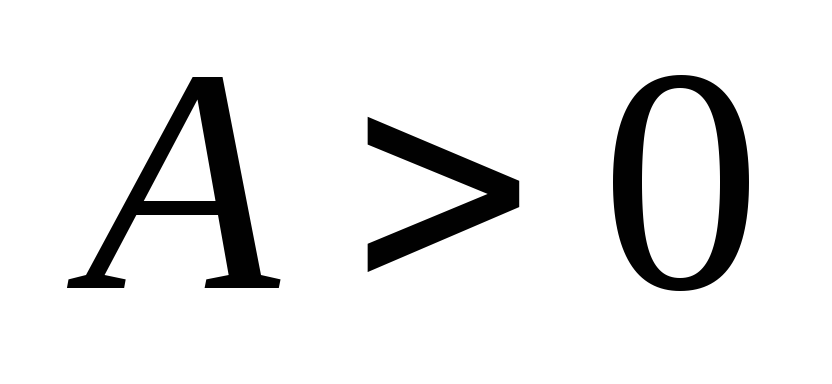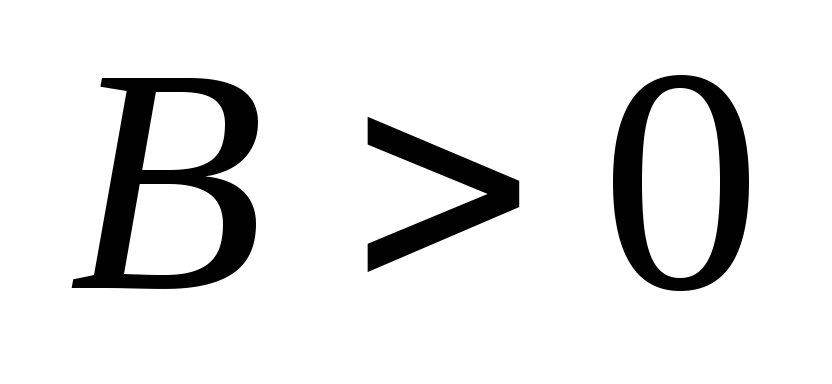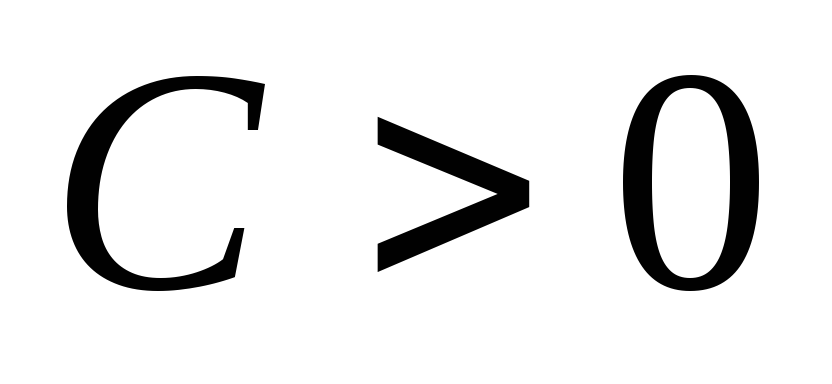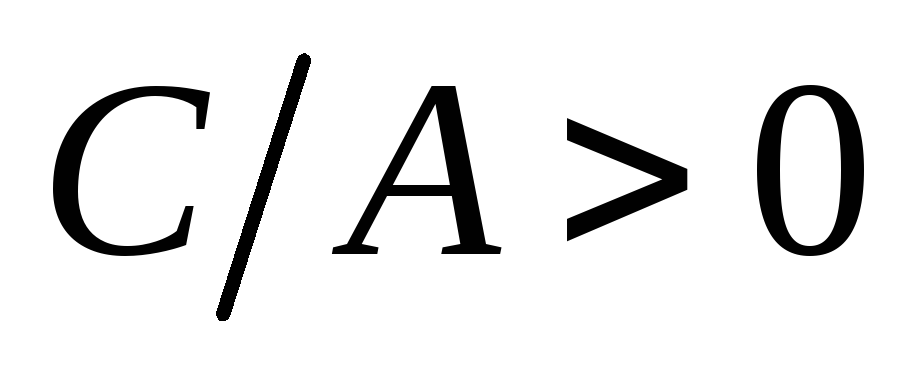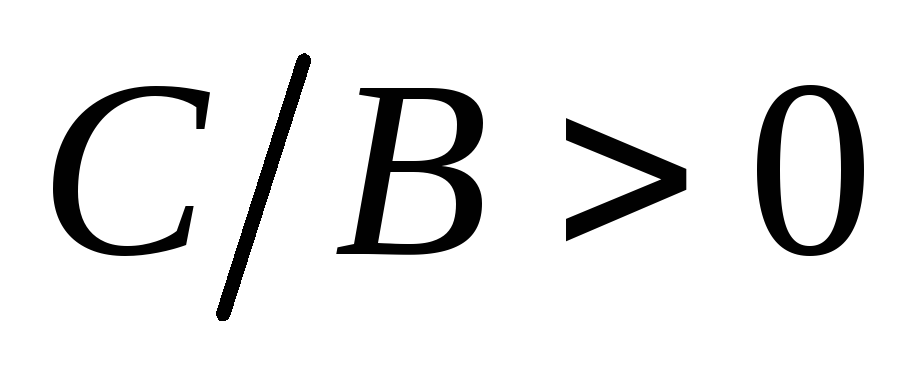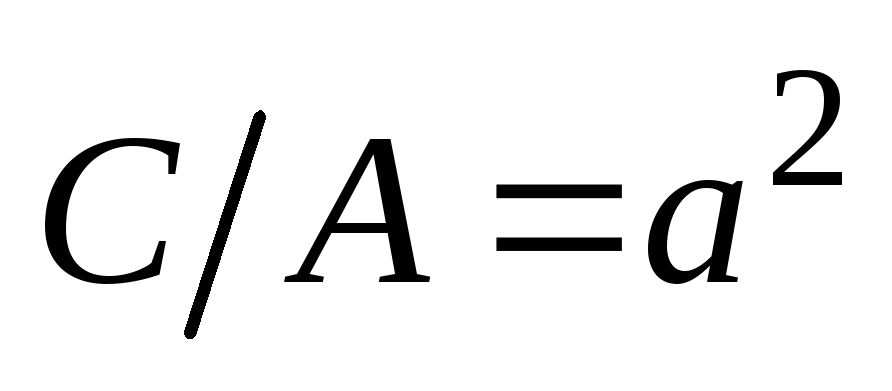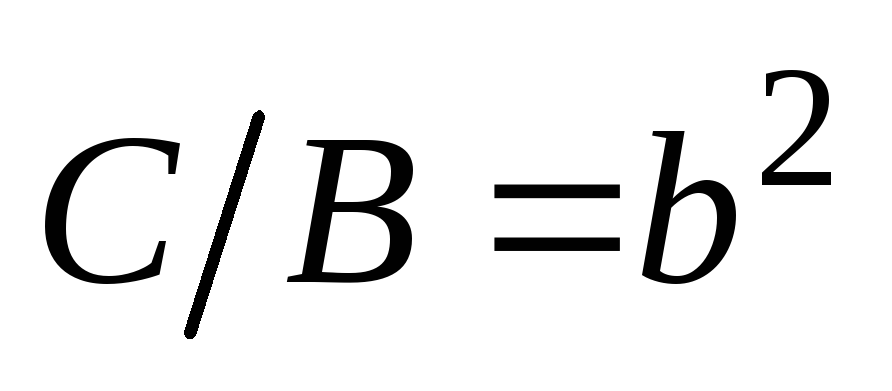1. Пусть . Так как , , , то , . Обозначив , , получим

.

(6.6)

Линия (рис.6.6), соответствующая уравнению (6.6), называется эллипсом, а само уравнение – каноническим уравнением эллипса. Числа

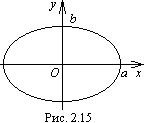
a и b называются полуосями эллипса.

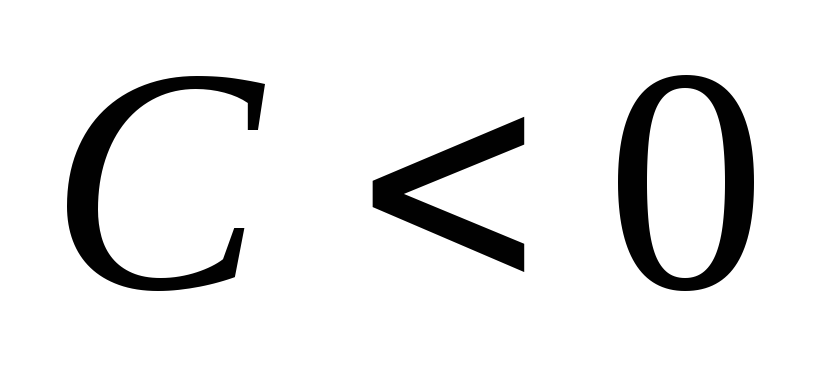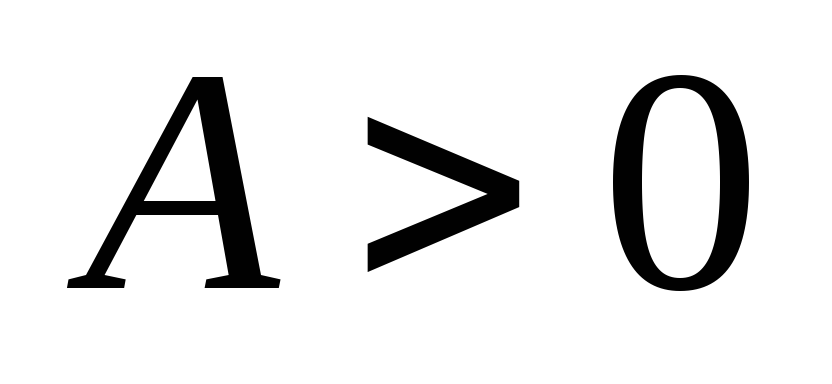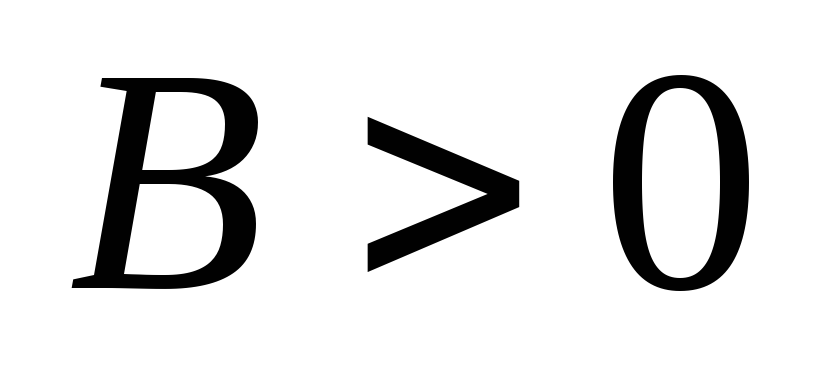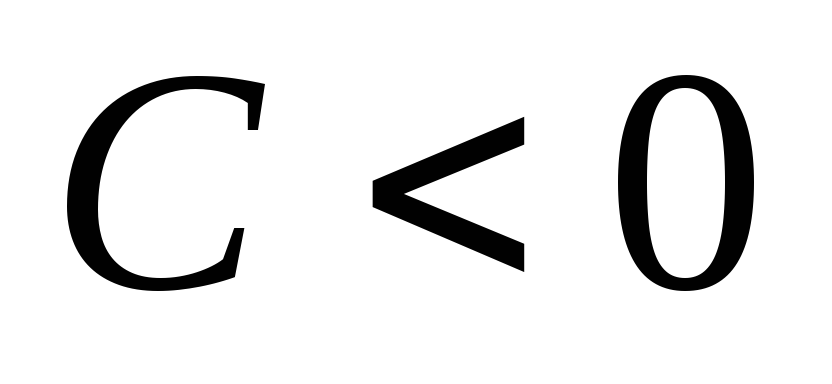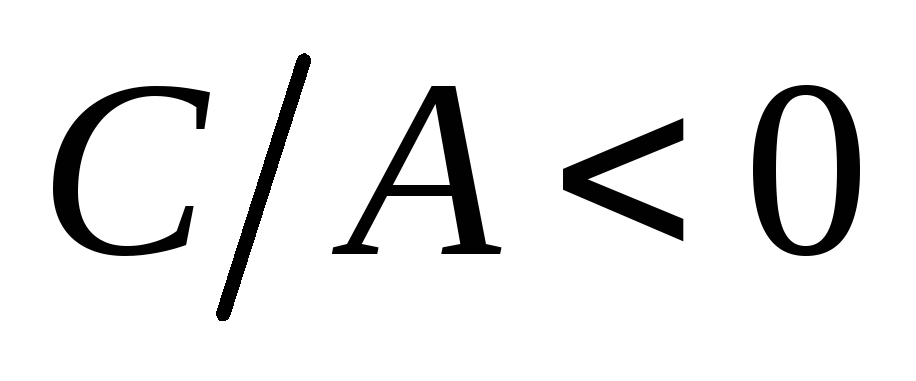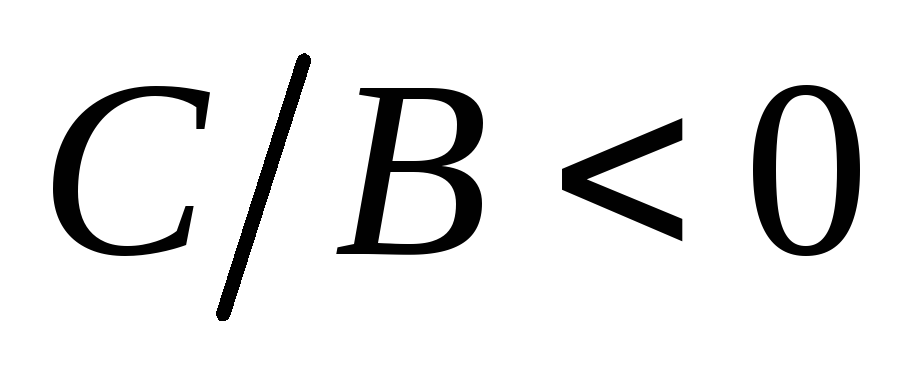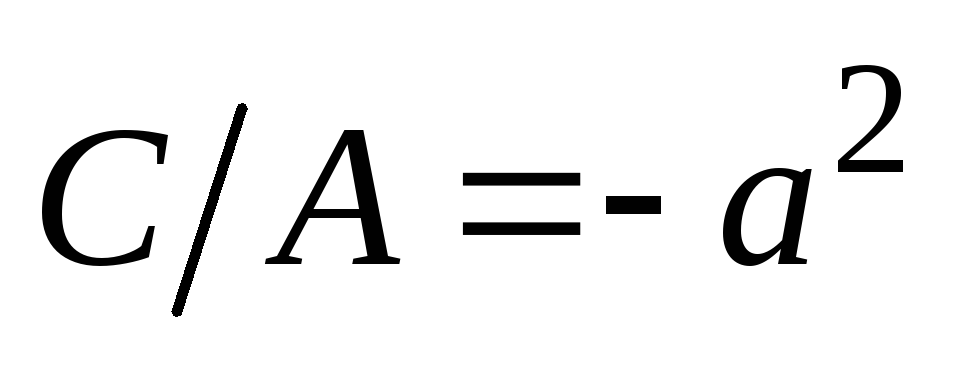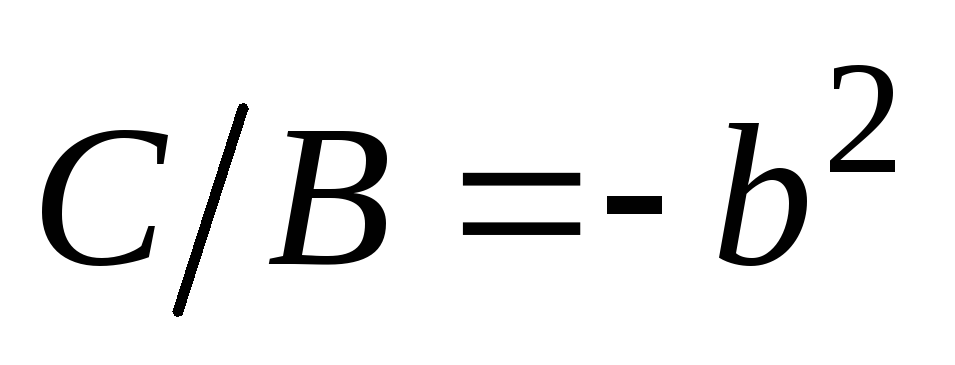2. Пусть . Так как , , , то , . Обозначив , , получим

,

или

.

(6.7)

Уравнение (6.7) называют уравнением мнимого эллипса, т.к. нет ни одной точки, координаты ко­торой удовлетворяли бы данному уравнению.

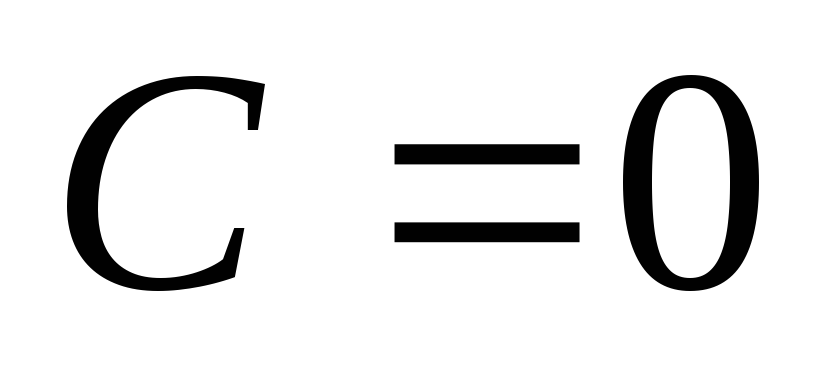3. Пусть . Уравнение имеет вид

,

(6.8)

где , . Уравнение (6.8) определяет только одну точку плоскости (0;0).

Пример 6.4. Рассмотрим уравнение . Здесь

, , . Разделив обе части уравнения на 16, приведем его к каноническому виду:

.

Сравнивая полученное уравнение с уравнением (6.6), видим, что это эллипс с полуосями , .

Рассмотрим уравнение эллиптического типа, в котором коэффициенты при квадратах неизвестных равны. Оно имеет вид , где , . Преобразуем уравнение к виду . Так как , можно ввести обозначение . Уравнение примет вид . Это уравнение окружности.

Рассмотрим уравнение гиперболического типа. Если , то обе части уравнения можно разделить на С. Тогда урав­нение примет вид

,

или

.

Будем считать, что и , в противном случае, умножим обе части этого урав­нения на –1.

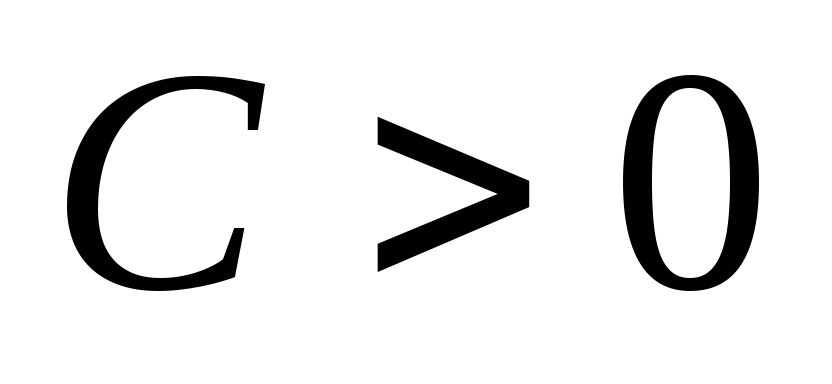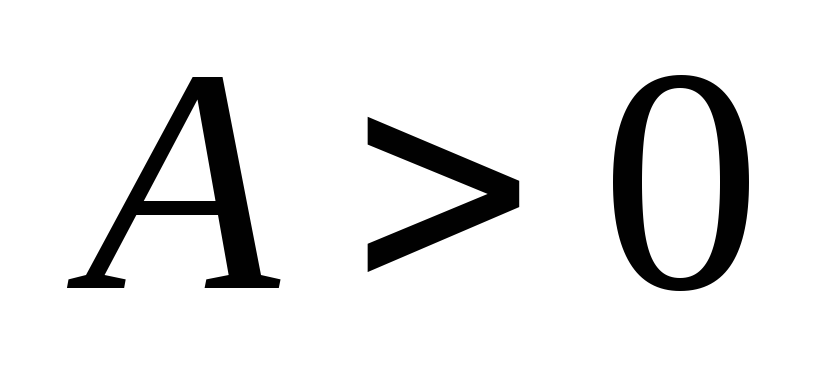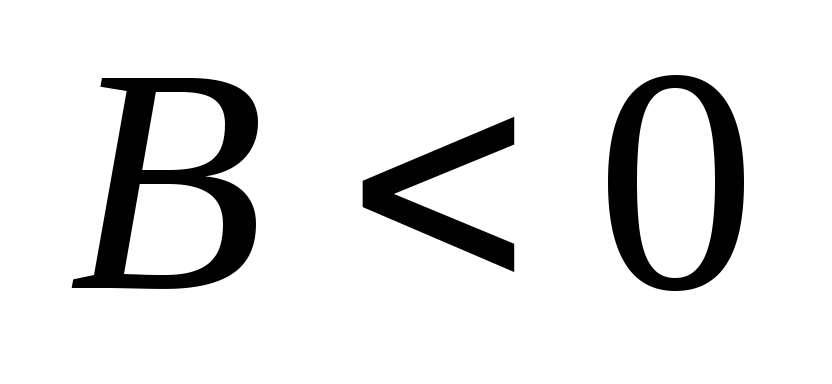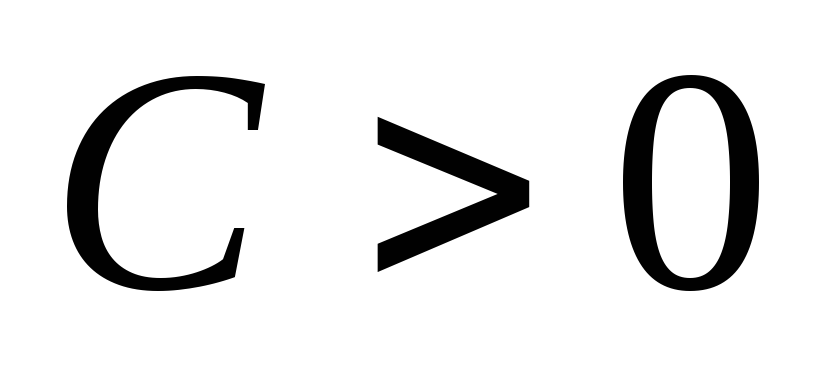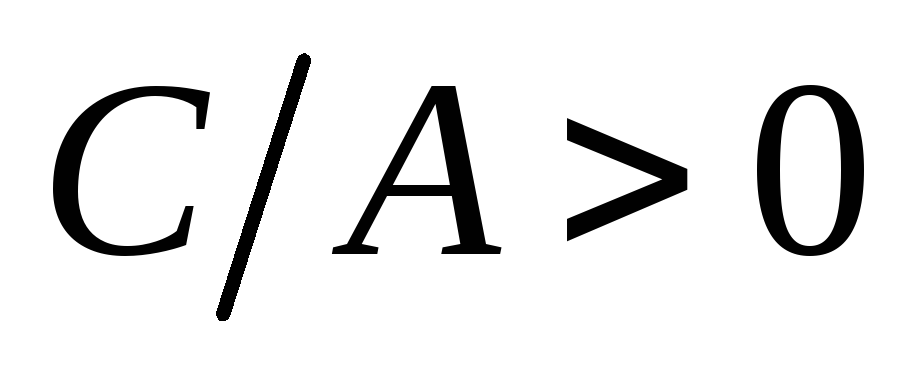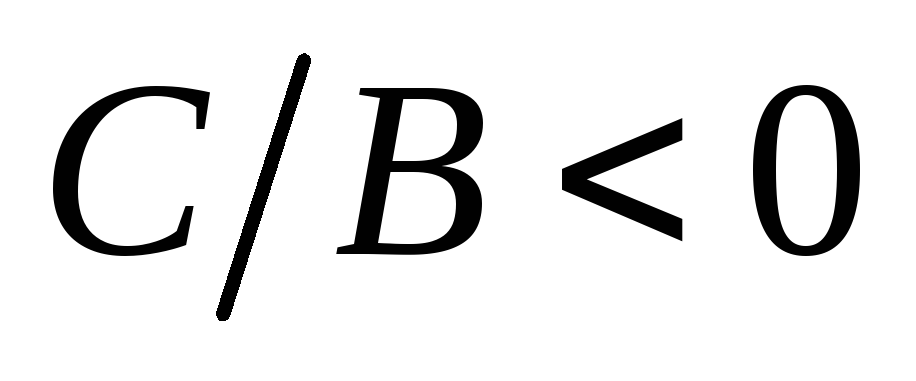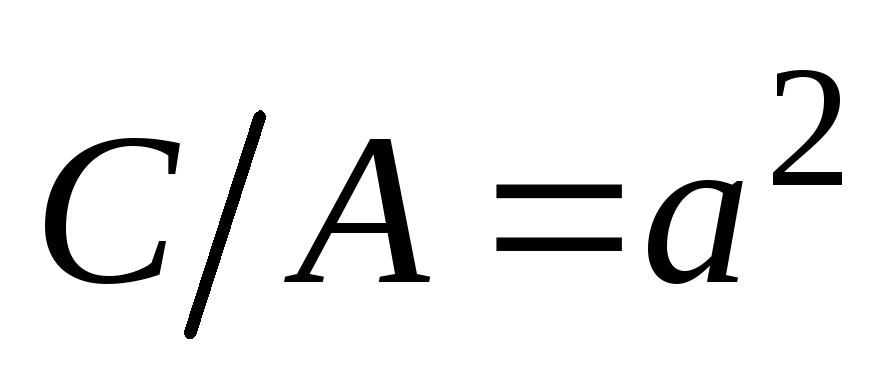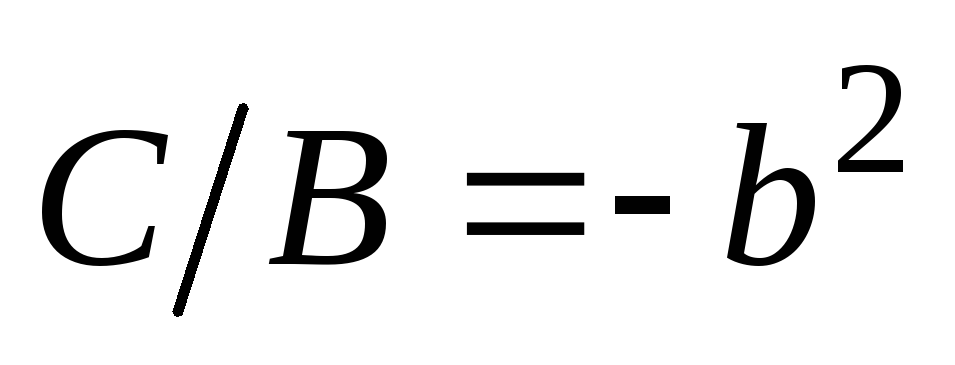1. Пусть . Так как , , , то , . Обозначив , , получим

,

(6.9)

Линия (рис.6.7), соответствующая уравнению (6.9), называется гиперболой, а само уравнение – каноническим уравнением гиперболы. Число а называется действительной полуосью гиперболы, число b – мнимой полуосью.

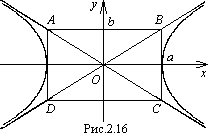
Асимптоты гиперболы

,

это диагонали прямоугольника , центр которого находится в начале координат, а стороны параллельны осям координат и равны и (рис.6.7).

Вычерчивание гиперболы по ее уравнению лучше всего начи­нать с построения этого прямоугольника. Затем нужно провести асимптоты и после этого построить кривую.

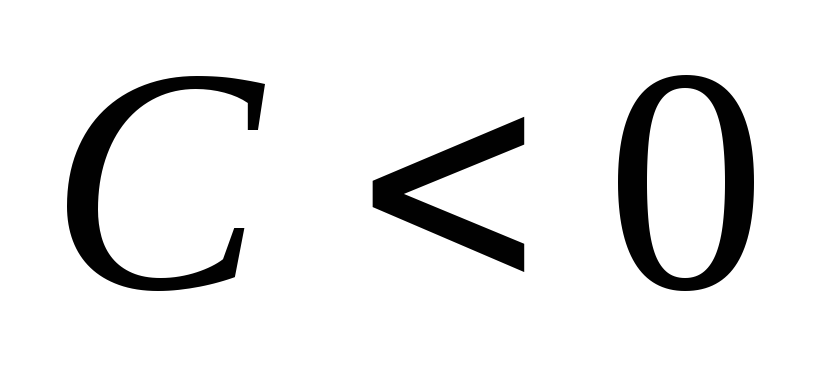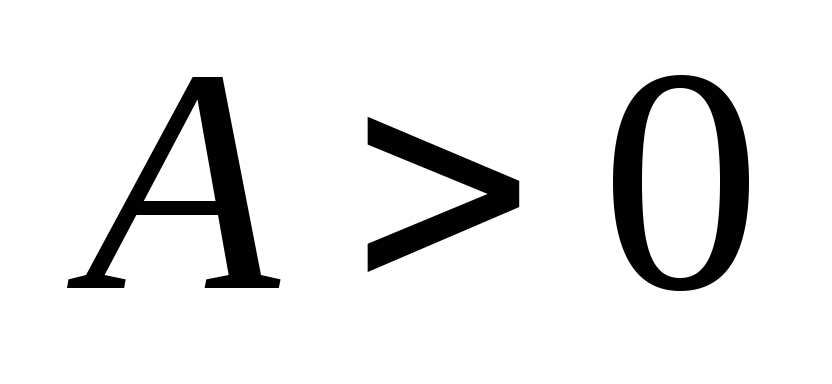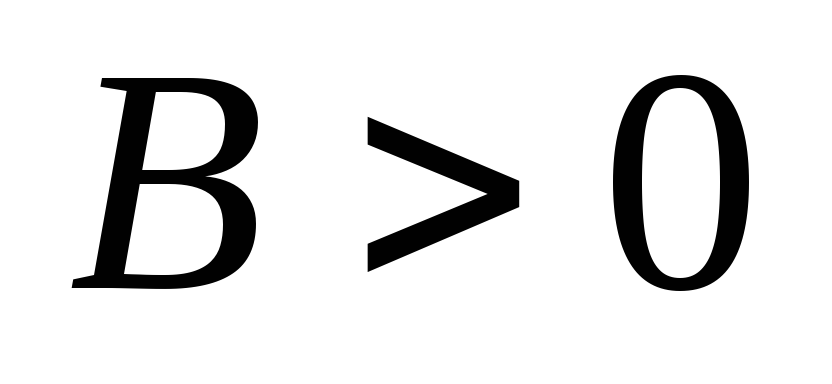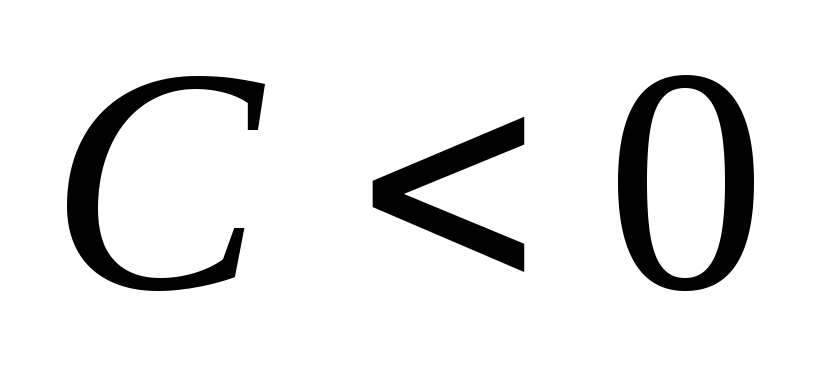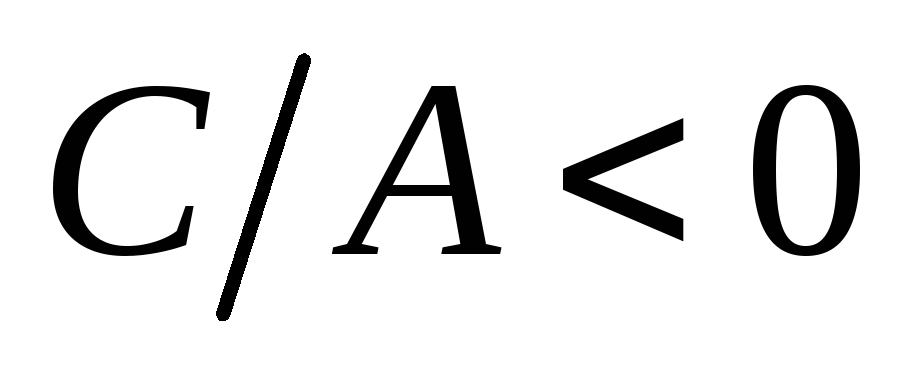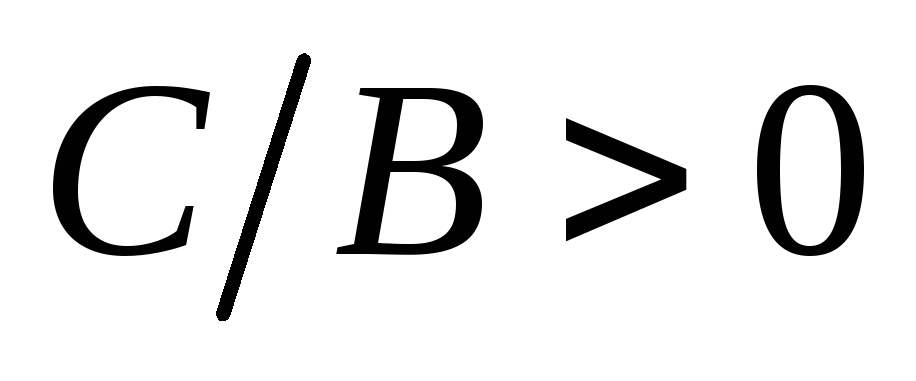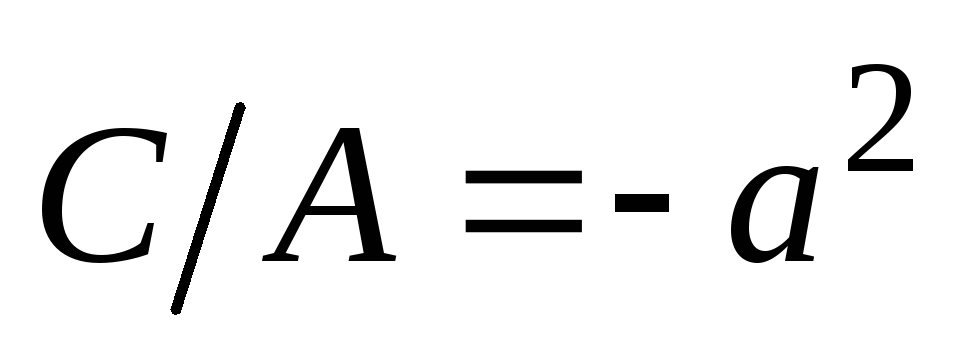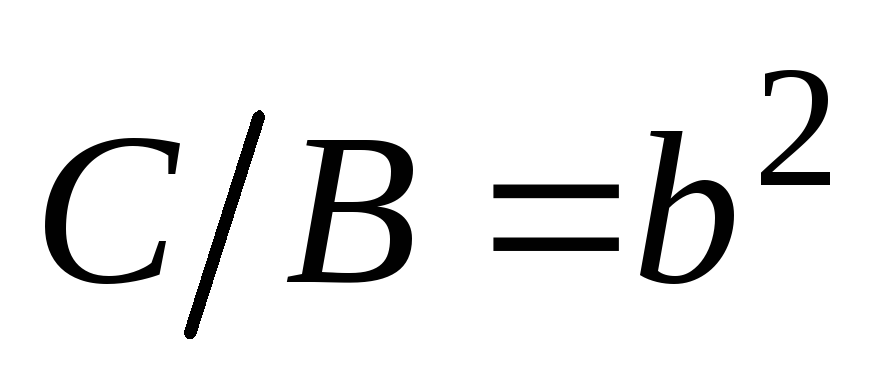2. Пусть . Так как , , , то , . Обозначив , , получим

.

(6.10)

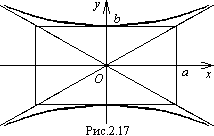
Уравнение (6.10) называют уравнением сопряженной гиперболы (рис.6.8).

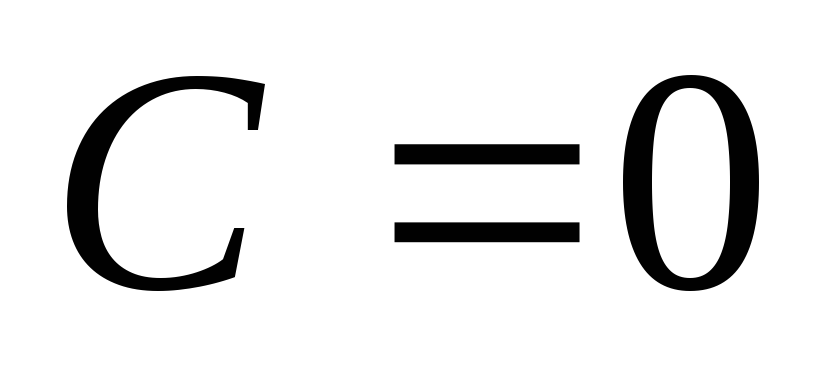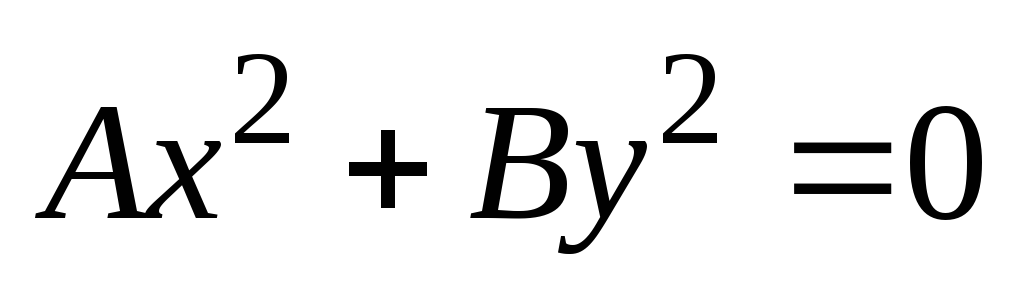3. Пусть . Уравнение имеет вид , где , .

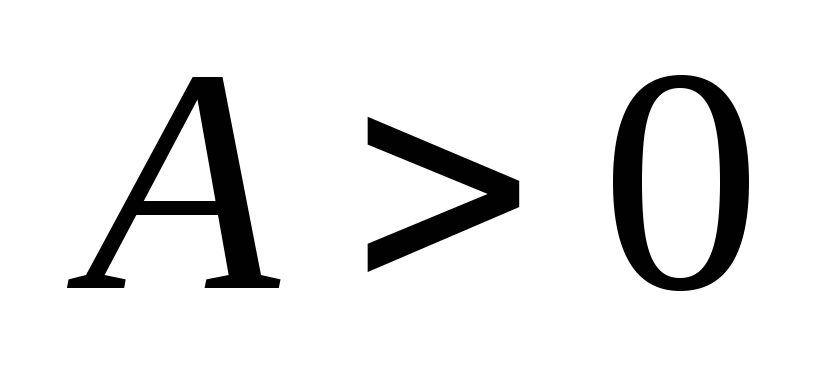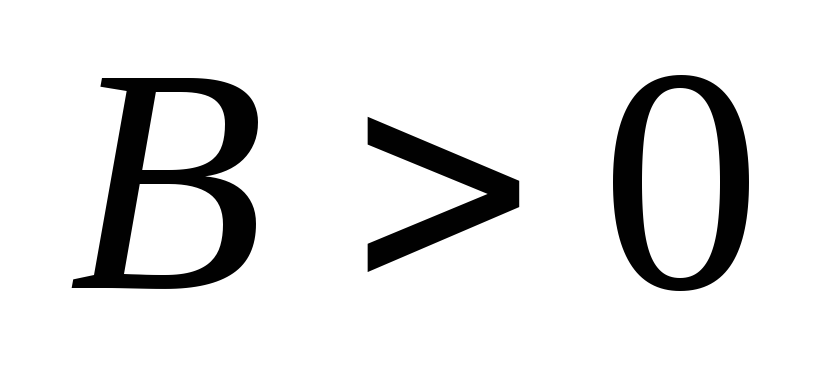Введем обозначения , , получим

,

откуда

,

или

.

Это пара прямых, пересекающихся в начале координат.

Пример 6.5. Рассмотрим уравнение . Здесь , , . Разделив обе части уравнения на 36, приведем его к каноническому виду:

.

Сравнивая полученное уравнение с уравнением (6.9), видим, что это гипербола с полуосями , .

Рассмотрим линии параболического типа. Это линии, в уравнение которых одно неизвестное входит в квадрате, а другое – в первой степени или отсутствует.

Допустим, уравнение имеет вид , где .

1. Пусть 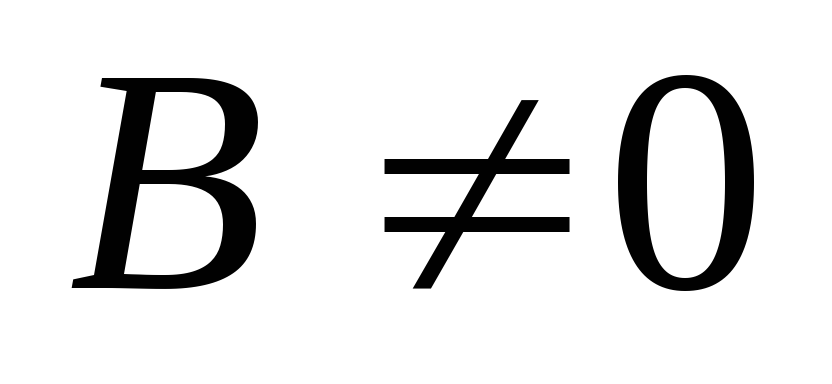. Разрешим уравнение относитель­но у:

.

Обозначив , , получим уравнение

.

(6.11)

Это парабола, график которой симметричен относительно оси (рис.6.9).

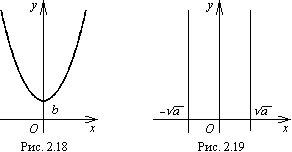
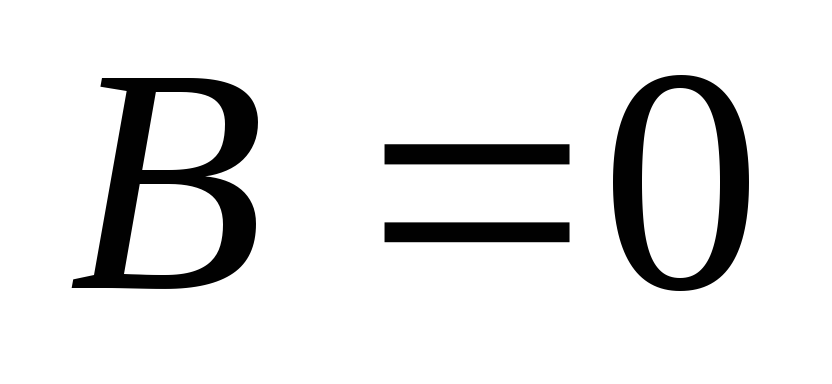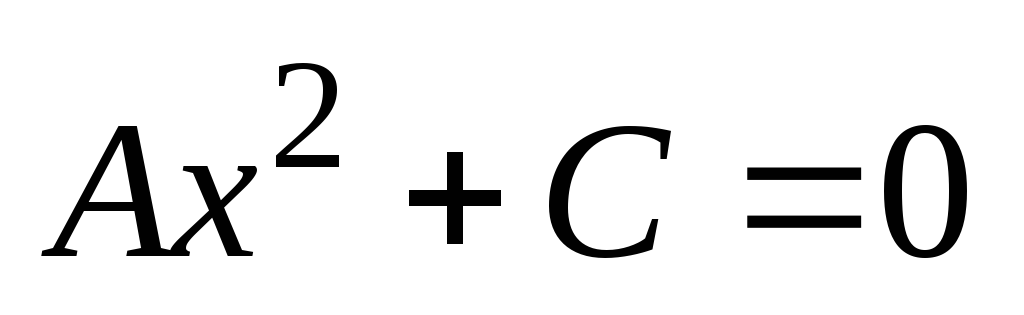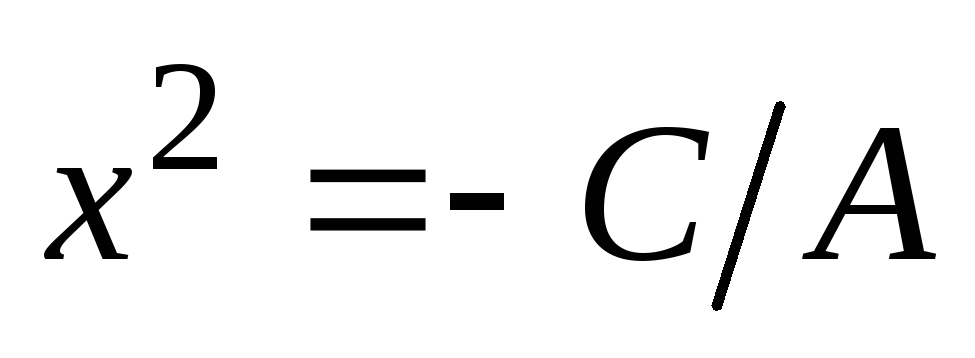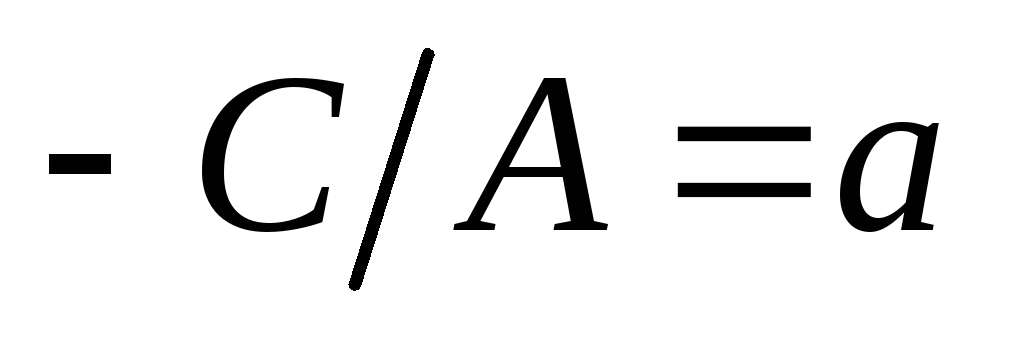2. Пусть . Уравнение примет вид , или . Обозначив , получим .

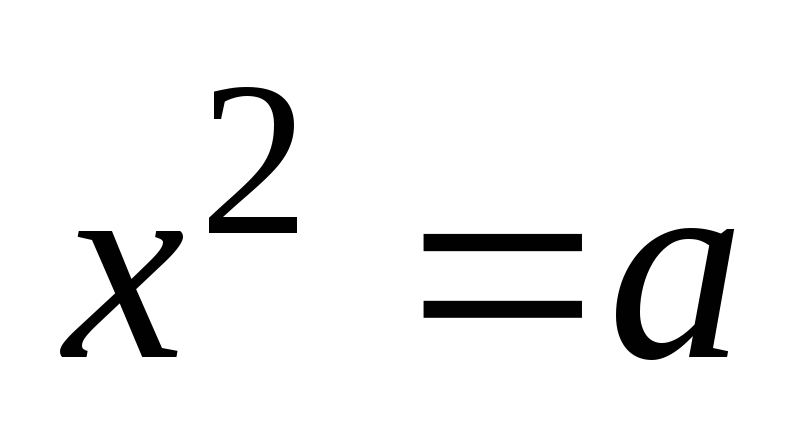Если , то . Это пара прямых и , параллельных оси и расположенных симметрично относительно этой оси (рис.6.10).

Если , то . Это пара совпадающих прямых , т.е. ось .

Если , то при уравнение не удовлетворяется ни при каких значениях переменной x. Такое уравнение определяет пустое множество точек. Можно сказать, что это пара мнимых прямых.

Пример 6.5. Рассмотрим уравнение . После исключения первой степени неизвестной уравнение примет вид . Сравнивая полученное уравнение ис уравнением (6.11) видим, что это уравнение параболы, симметричной относительно оси .

Аналогично проводится исследование уравнения параболического типа, содержащего :

.

В этом случае получатся такие же линии, но симметричные относительно оси .

УПРАЖНЕНИЯ

6.6. Написать уравнение окружности с центром C(3;4) и радиусом 5. Лежат ли на этой окружности точки A(-1;1), B(2;3), O(0;0) и D(4;1)?

6.7. Построить окружности:

1) ;

2) ;

3) .

6.8. Построить окружность , прямую и найти точки их пересечения.

6.9. Построить линии:

1); 2); 3); 4);

5); 6);

7) ; 8) ;

9) ; 10) .

11) ; 12) ; 13) ;

О Т В Е Т Ы К У П Р А Ж Н Е Н И Я М