Глава 5

5.11. а) 10; б) . 5.12. 137. 5.13. 39. 5.15. С(1;6). 5.16. А(-3;1). 5.17. (-1;8), (1;9), (3;10). 5.18. (1;4) и (13;16)

5.19. 5.20 , D и E лежат.

5.21. 5.22. 5.23. .

5.24. 5.25. , . 5.26. .

5.27. . 5.28. .

5.30. 1) , 2) . 5.31. 5.32. 5.33. 1), 2) , 3) , 4) . 5.34. Точки A и C лежат на прямой, точка B не лежит. 5.35. 1) , 2) , 3), 4) . 5.36. А(1;2). 5.37. 1) , 2) , 3) . 5.38. 1) , 2) , 3) , 4) . 5.39.. 5.40. . 5.41. 1) , 2) , 3) . 5.42. 1) ; 2) ; 3) ; 4) . 5.43., , . 5.44. 1) , 2) . 5.45. 1) , 2) .5.46. 2,8; 0; 1,4. 5.47. 3. 5.48. . 5.49., , . 5.50. (3;-1), (3;3), ;, , . 5.51. .

Глава 6. Кривые второго порядка

6.1. Преобразования системы координат

В системе координат положение каждой точки полно­стью определяется заданием ее координат. Если выбрать другую систему координат, то координаты точек в ней изменятся. При смене системы координат меняются и уравнения линий. В связи с этим встает задача: вы­брать систему координат так, чтобы рассматриваемая линия имела в ней самое простое уравнение. Для этого необходимо знать формулы преобразования координат при переходе от одной системы к другой.

Пусть – исходная система координат, – нoвая си­стема координат (рис.6.1).

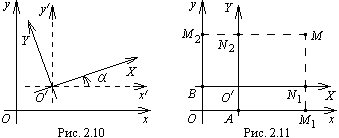
Проведем через точку прямые, парал­лельные осям Ох и Оу, получим систему коорди­нат . Система полу­чается из х′О′у′ при повороте осей и на угол . Таким образом, переход от данной системы координат к новой системе совершается с помощью двух движений: параллельного переноса и поворота.

1. Пусть 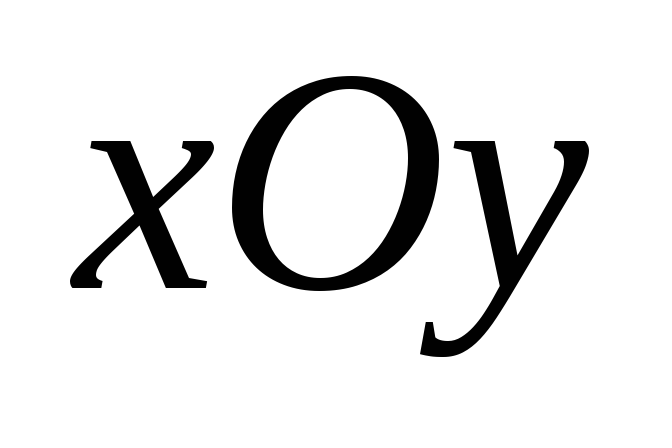– данная система координат; 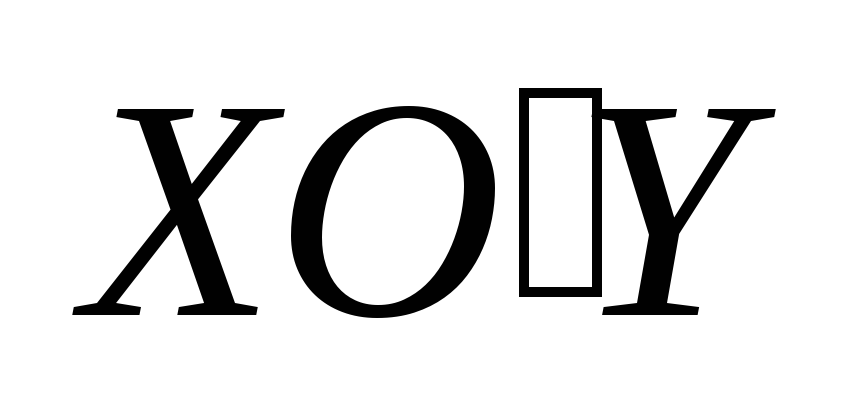– система, которая получается из 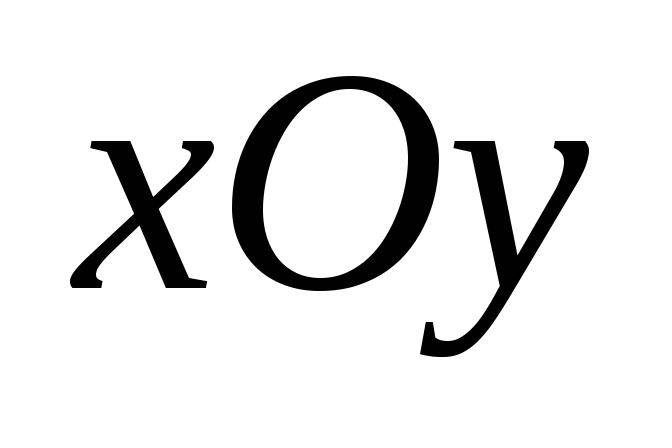при параллельном переносе (рис.6.2). Положение новой системы определяется координатами точки – центра новой системы. Точ­ка в системе 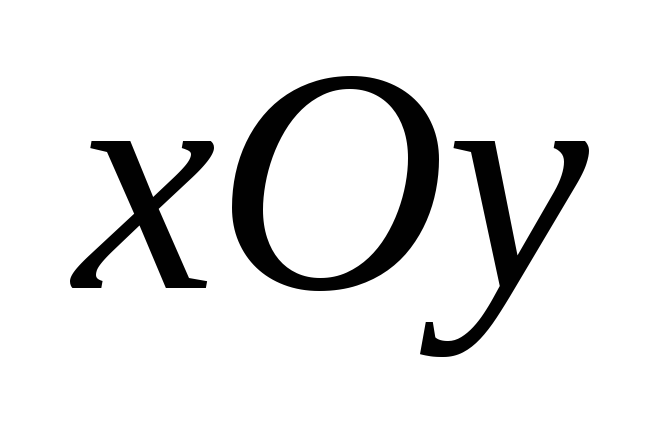имеет координаты 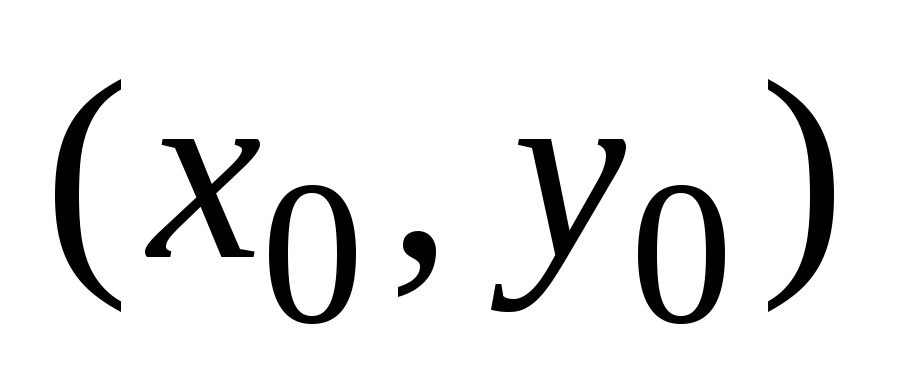. Следовательно, , .

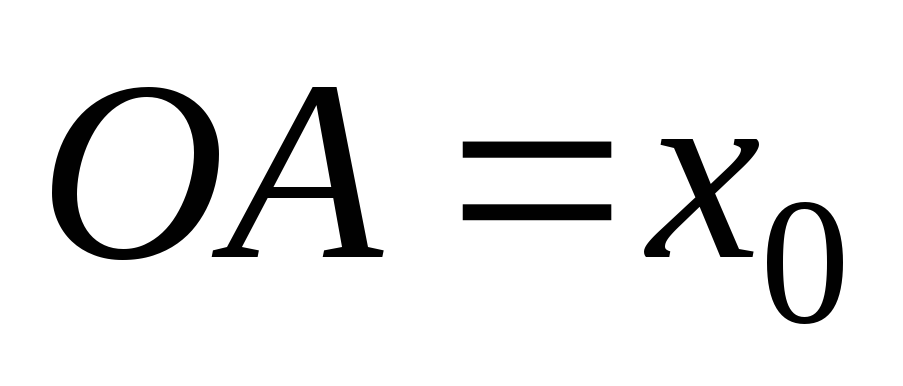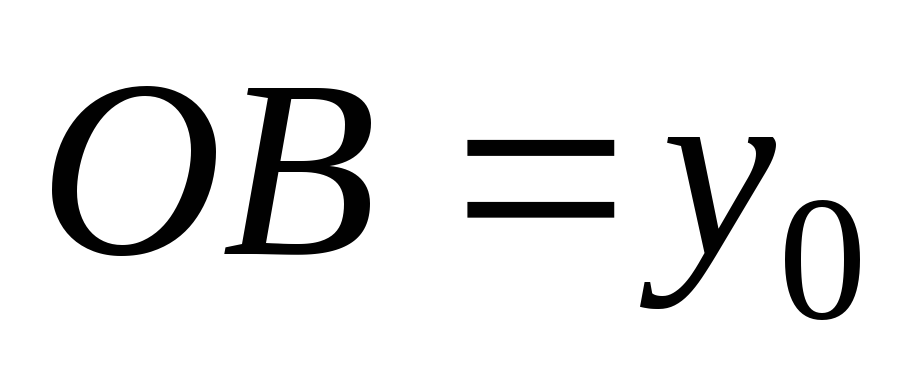Рассмотрим произвольную точку М. В си­стеме точка М имеет координаты . Следовательно, = х, = y. В новой системе точка М имеет координаты , т.е. . Очевидно, , .

Учитывая, что , , получаем

, ,

или

(6.1)

которые называются формулами параллельного переноса системы координат.

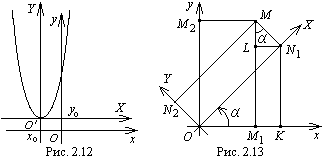
Пример 6.1. Рассмотрим уравнение параболы . Выражение дополним до полного квадрата:

,

откуда

,

или

.

Введем новые координаты , . В системе координат данное уравнение имеет простой вид .

По формулам параллельного переноса (6.1) находим координа­ты нового центра О′ в старой системе: , (рис.6.3).

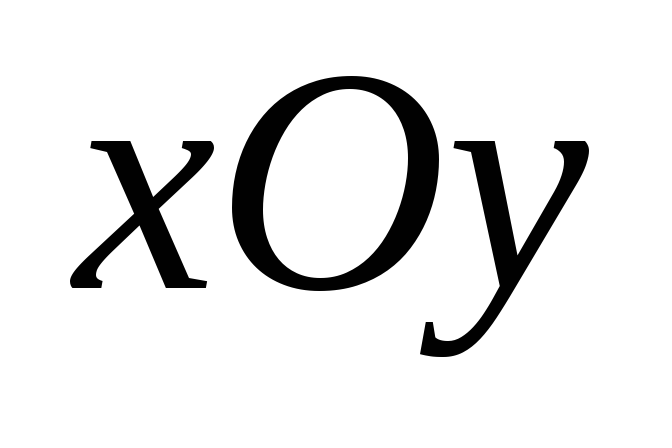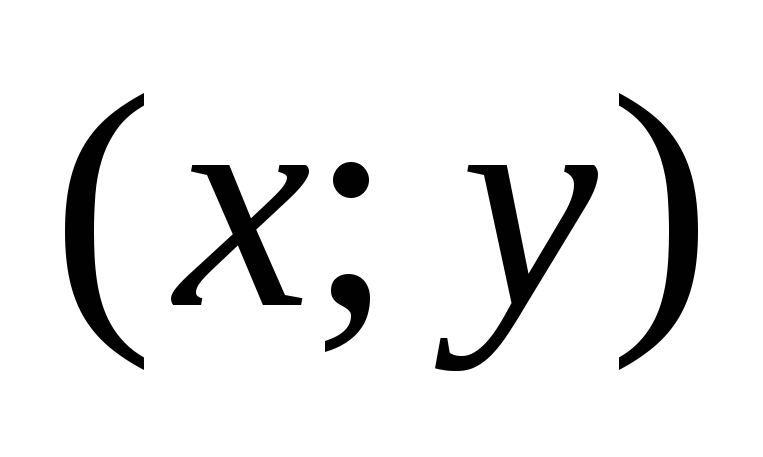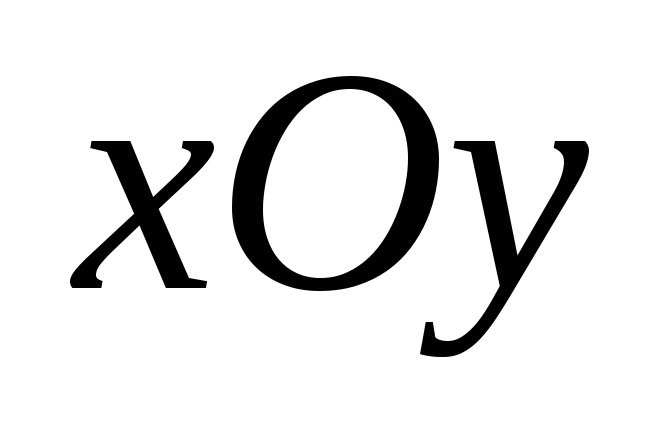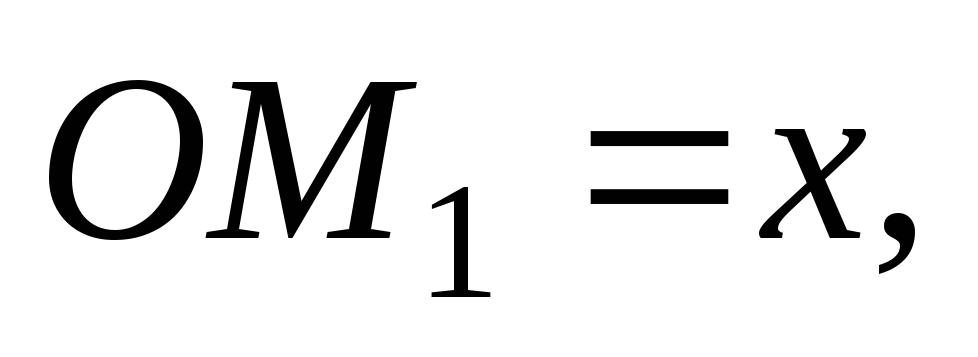
2. Дана система координат и новая система , полученная из поворотом на угол (рис. 6.4). Пусть М – произвольная точка плоскости с координатами в системе , т.е. 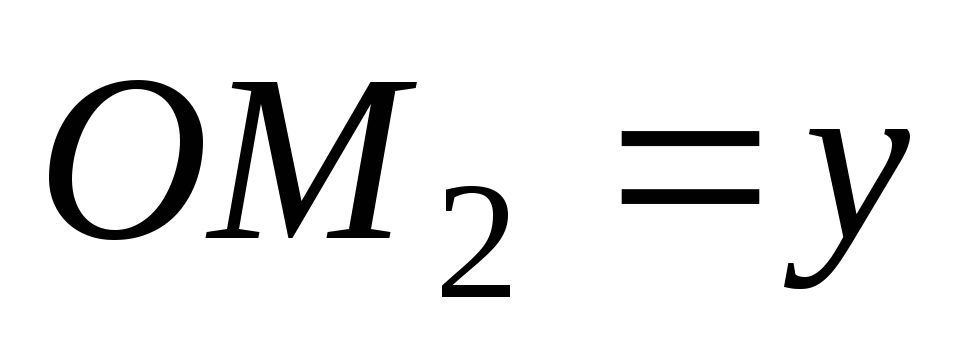. Пусть 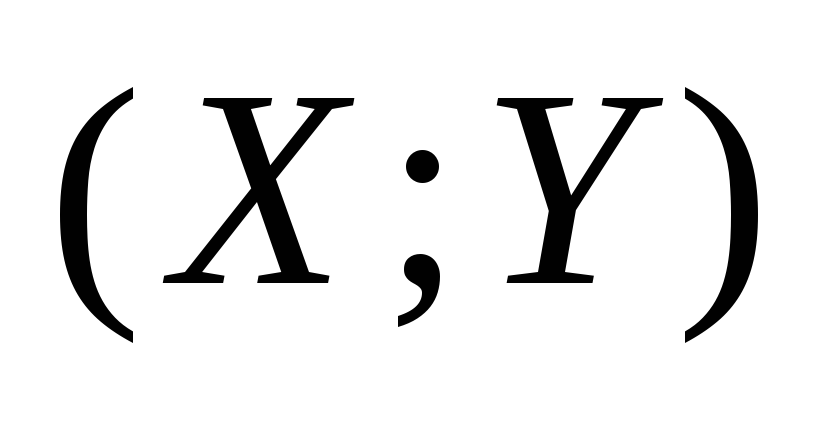– координаты точки М в новой си­стеме координат, следовательно, 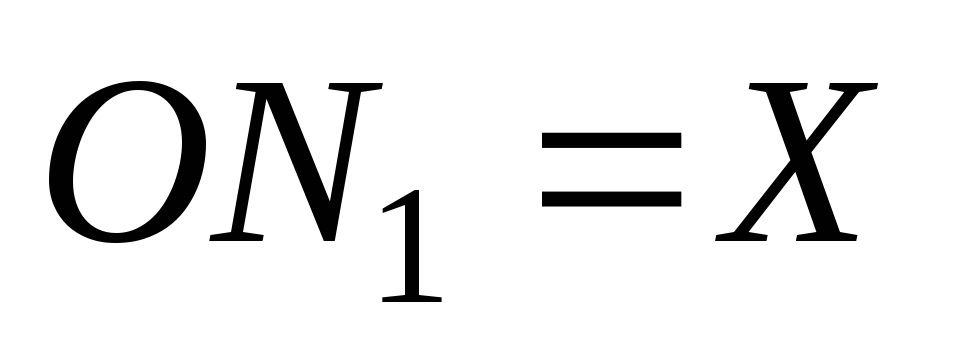, 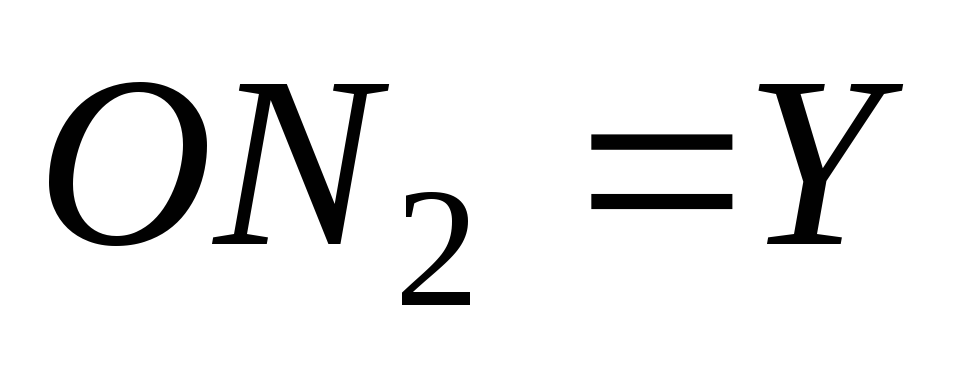. Из точки 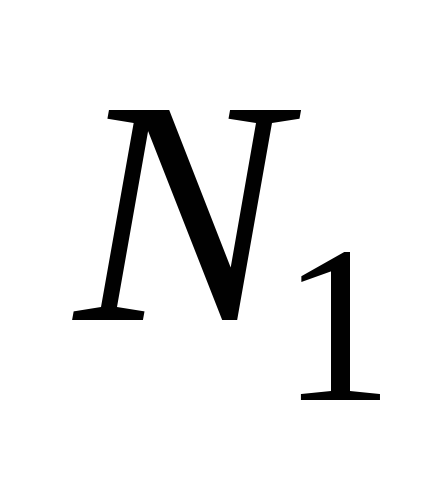опустим перпендикуляр 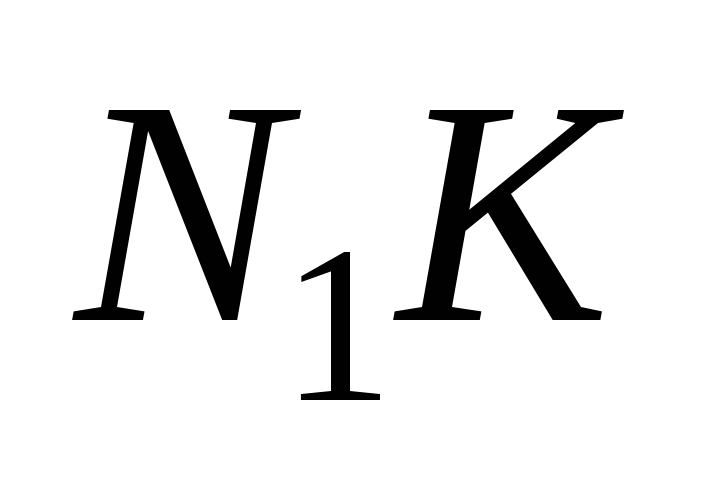на ось 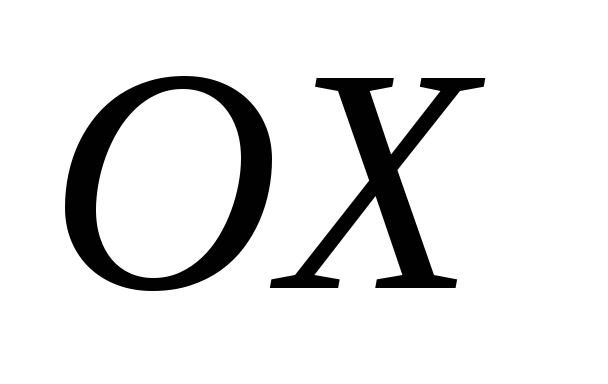, тогда

.

Из треугольника получаем

.

Проведем отрезок параллельно оси . Из треугольника получаем , т.к. . Поскольку , . Подставляя найденные выражения в равенство (5.13), получаем формулу для координаты х. Аналогично выводится формула для координаты y.

(6.2)

Равенства (6.2) являются формулами для поворота системы координат на угол .

Пример 6.2. В системе хОу кривая задана уравнением . Повернем систему координат на . Для этого воспользуемся формулами (6.2)

, ,

или

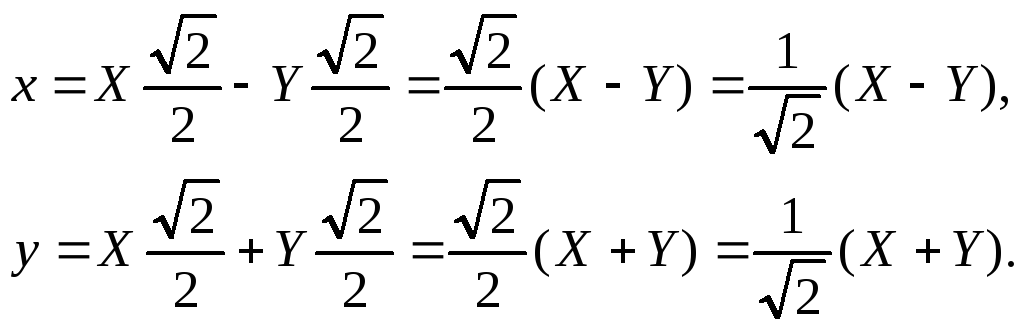
Следовательно,

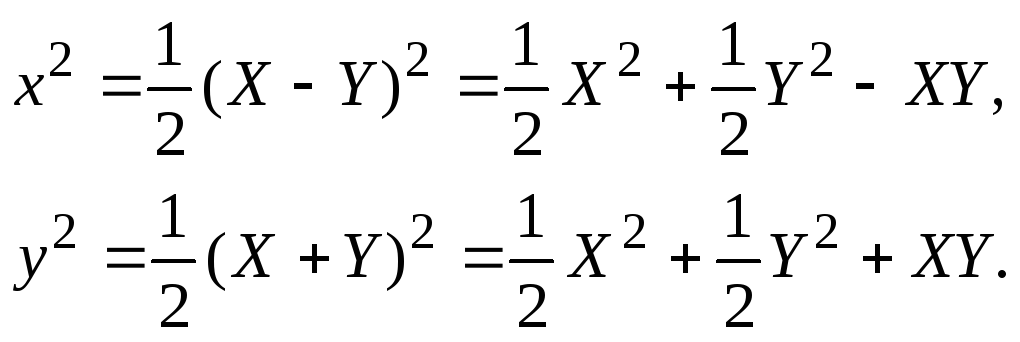
Данное уравнение в новой системе координат имеет вид –2XY = 1, или . Это уравнение гиперболы, изображенной на рис.6.5.