5.5. Расстояние от точки до прямой

Пусть даны точка и прямая . Под расстоянием от точки до прямой понимается длина перпендикуляра , опушенного из точки на прямую (рис. 5.15). Для определения расстояния необходимо:

1. составить уравнение прямой 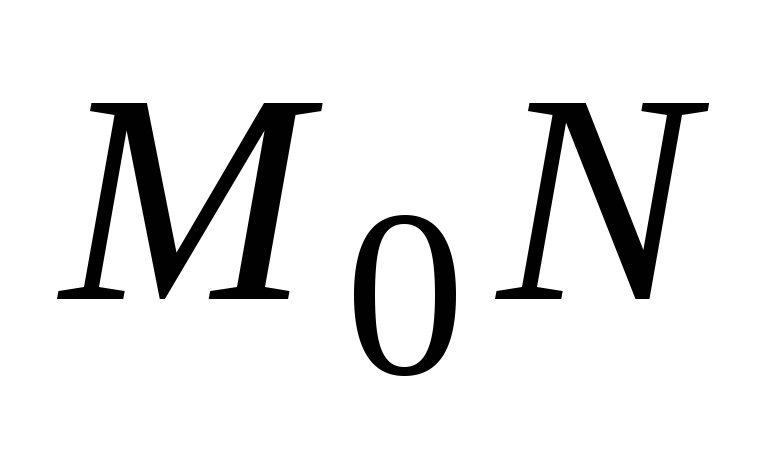, перпендикулярной данной и проходящей через точку ;

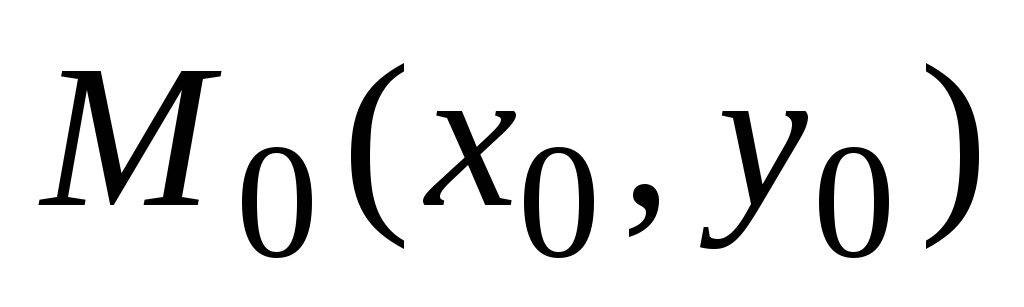2. найти точку 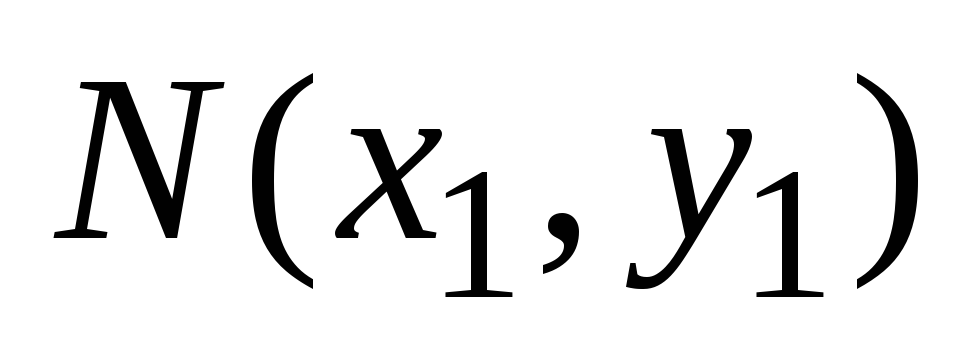пересечения прямых, решив систему уравнений этих прямых;

3. по формуле (5.1) найти расстояние между двумя точками, т.е. найти .

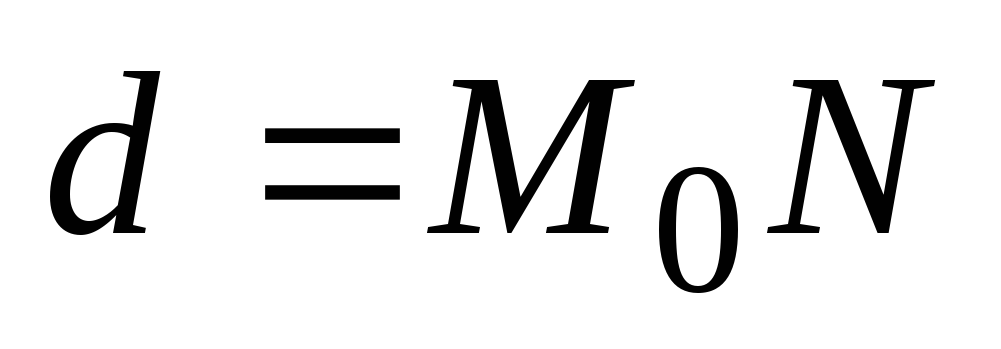В результате преобразований получим:

.

(5.18)

Пример 5.10. Найдем расстояние между точкой А(4;5) и прямой .

УПРАЖНЕНИЯ

5.11. Найти расстояние между точками:

а) А(3;8), В(-5;14);

б) С(-2;3), D(5;4).

5.12. Вычислить площадь квадрата, две смежные вершины которого А(3:-7), В(-1;4).

5.13. Вычислить периметр правильного треугольника, две смежные вершины которого А(3;14), В(-2;2).

5.14. Показать, что треугольник АВС равнобедренный, если А(2;-1), В(4,2), С(5;1).

5.15. Даны точки А(-2;5) и В(4;17). Найти координаты точки С, делящей отрезок АВ пополам.

5.16. Точка С(2;3) является серединой отрезка АВ. Определить координаты точки А, если координаты точки В(7;5).

5.17. Даны точки А(-3;7) и В(5;11). Отрезок АВ точками разделен на четыре равные части. Найти координаты точек деления (двумя способами).

5.18. Даны точки А(-2;1) и В(3;6). Найти точку С, делящую отрезок АВ в отношении 1) ; 2) .

5.19. Найти уравнение множества точек, равноудаленных от точки А(-4;2) и точки В(-2;-6).

5.20. Написать уравнение линии, по которой движется точка , равноудаленная от точек A(0;2) и B(4;-2). Лежат ли на этой линии точки C(-1;1), D(1;-1), E(0;2) и F(2;2)?

5.21. Вывести уравнение линии, по которой движется точка М, если в каждый момент она находится вдвое ближе к точке А(2;0), чем к точке В(8;0).

5.22. Написать уравнение траектории точки М, которая при своем движении остается втрое дальше от тоски А(0;9), чем от точки В(0;1).

5.23. Написать уравнение траектории точки М, которая при своем движении остается вдвое ближе к точки А(-1;1), чем к точке В(-4;4).

5.24. Найти уравнение множества точек, равноудаленных от оси Oy и точки F(4;0).

5.25. Написать уравнение линии, по которой движется точка М, оставаясь вдвое дальше от оси Ох, чем от оси Оу.

5.26. Написать уравнение геометрического места точек, равноудаленных от точки F(2;2) и от оси .

5.27. Написать уравнение линии, по которой движется точка , оставаясь вдвое дальше от оси , чем от оси .

5.28. Написать уравнение линии, по которой движется точка , оставаясь вдвое дальше от оси , чем от прямой .

5.29. Определить вид линий и построить их:

1)

2)

3)

4)

5.30. Дано общее уравнение прямой . Написать:

1) уравнение с угловым коэффициентом;

2) уравнение прямой в отрезках.

5.31. Написать уравнение прямой, отсекающей на оси ординат отрезок и образующий с положительным направлением оси абсцисс угол .

5.32. Написать уравнение прямой, отсекающей на оси ординат отрезок и образующий с положительным направлением оси абсцисс угол .

5.33. Определить параметры k и b для каждой из прямых : 1), 2) , 3) , 4) .

5.34. Определить, какие из точек А(2;3), B(3;3), C(4;4) лежат на прямой

5.35. Найти угол между прямыми:

1) и ;

2) и ;

3) и ;

4) и .

5.36. Показать, что прямые и пересекаются и найти координаты точки пересечения.

5.37. Составить уравнение прямой, проходящей через точку А(2;3)

1) параллельно оси Ох;

2) параллельно оси Оу;

3) составляющей с осью Ох угол .

5.38. Составить уравнение прямой, проходящей через точки:

1) A(3;1), B(5;4);

2) A(3;1), C(3;5);

3) A(3;1), D(-4;1);

4) L(-1;3), N(2;5).

5.39. Построить прямую, проходящую через начало координат и точку A(-2;3) и написать ее уравнение.

5.40. Написать уравнение прямой, проходящей через точки А(-1;3) и В(4;-2).

5.41. Написать уравнение пучка прямых, проходящих через точку А(2;3). Выбрать из этого пучка прямые, составляющие с осью Ох углы:

1) ;

2) ;

3) и построить их.

5.42. Определить угол между прямыми:

1) , ;

2) , ;

3) , ;

4) , .

5.43. Среди прямых , , , указать параллельные и перпендикулярные.

5.44. Дана точка A(-2;5) и прямая . Написать уравнение пучка прямых, проходящих через точку A, и выбрать из пучка: 1) прямую, параллельную данной; 2) прямую, перпендикулярную к данной.

5.45. Уравнения прямых: 1) , 2) привести к виду в отрезках на осях.

5.46. Найти расстояние от точек K(4;3), L(2;1) и N(1;0) до прямой .

5.47. Найти расстояние от начала координат до прямой .

5.48. Показать, что прямые и параллельны и найти расстояние между ними.

5.49. В треугольнике с вершинами A(-2;0), B(2;6) и C(4;2) проведены высота BD и медиана BE. Написать уравнения стороны AC, медианы BE и высоты BD.

5.50. Определить вершины и углы треугольника, стороны которого заданы уравнениями , , .

5.51. Прямая пересекает оси и в точках A и B. Точка M делит AB в отношении . Написать уравнение перпендикуляра, восстановленного в точке M к прямой AB.

О Т В Е Т Ы К У П Р А Ж Н Е Н И Я М