5.4. Угол между прямыми. Условие параллельности и перпендикулярности прямых

Углом между двумя прямыми I и II называется угол, на который нужно повернуть прямую I про­тив часовой стрелки, чтобы она совпала с прямой II.

Пусть даны две прямые I: , которая наклонена к оси Ох под углом , и II: , которая наклонена к оси Ох под углом . Угол между ними обозначим через (рис. 5.11).

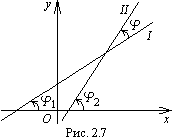
По свойству внешнего угла треугольника, , откуда . Если , то

,

или

.

(5.12)

Пример 5.5. Найдем угол между прямыми и . Подставив угловые коэффициенты и в формулу (5.12), получим

; .

Если прямые I и II взаимно перпендикулярны, то , откуда . Следовательно, и , или

.

(5.13)

Равенство (5.13) является условием перпендикулярности двух прямых.

Пример 5.6. Прямые и взаимно перпендикулярны, т.к. .

Рассмотрим две параллельные прямые и m (рис.5.12).

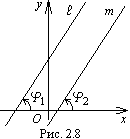
Т.к. углы и равны, то и

.

(5.14)

Равенство (5.14) является условием параллельности двух прямых.

Пример 5.7. Прямые и параллельны, т.к. .

5.5. Различные виды уравнения прямой

При решении задач используются различные виды уравнения прямой.

1. Пусть задан угол 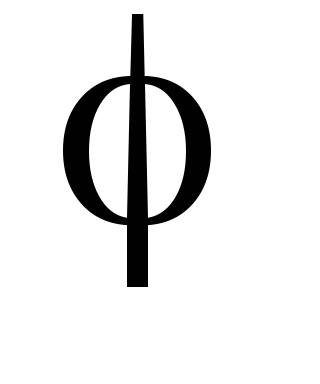, который прямая составляет с осью Ох, т. е. известен угловой коэффициент 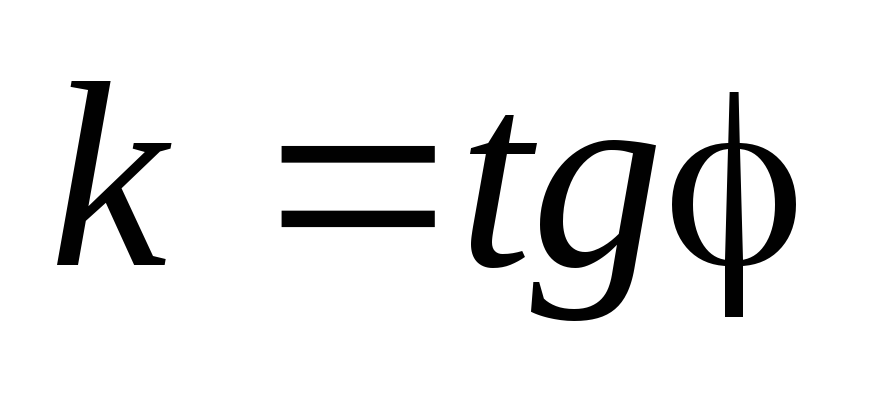и задана точка 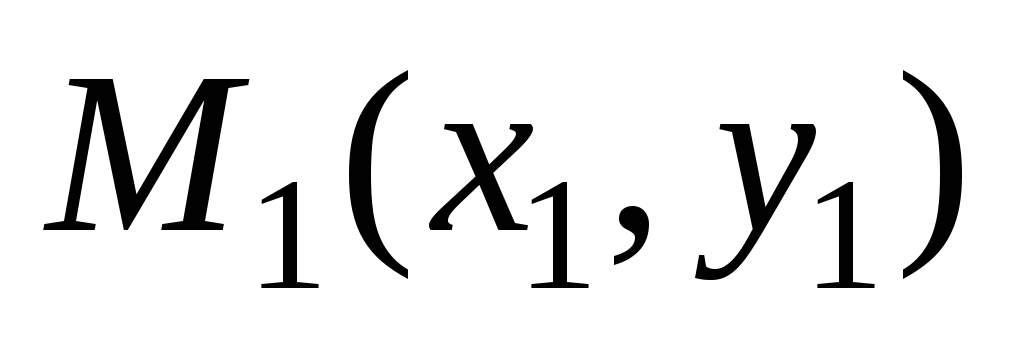, через которую проходит прямая. Уравнение прямой имеет вид 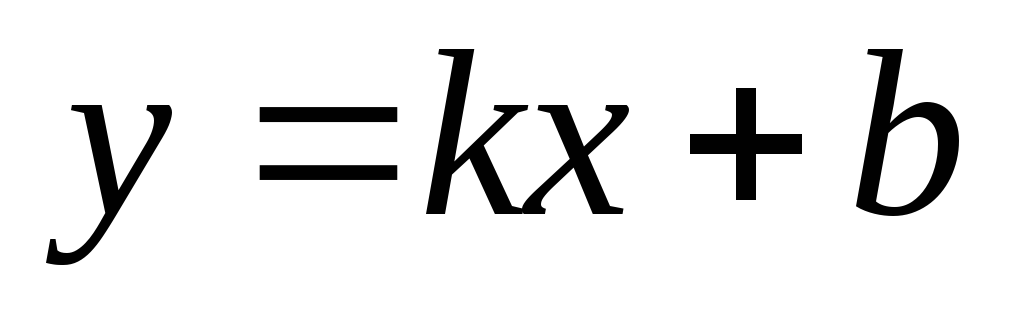, где k – заданная величина, значение b не известно. Так как пря­мая проходит через точку 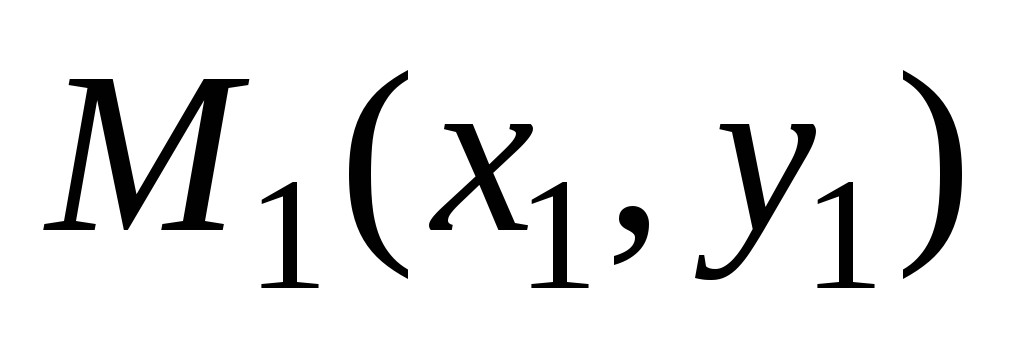, ее координаты удовлетво­ряют уравнению прямой. Отсюда следует равенство

,

из которого находим величину b

.

Подставив найденное значение b в (5.7), получим

,

или

,

откуда получаем уравнение прямой линии, проходящей через данную точку в данном направлении

.

(5.15)

Совокупность всех прямых плоскости, проходящих через одну точку называется пучком прямых, а точка - центром пучка. Если в уравнении (5.15) коэффициент k считать переменной величиной, то (5.15) будет являться уравнением данного пучка прямых.

Пример 5.8. Напишем уравнение прямой, проходящей через точку (–2, 5) и составляющей с осью Ох угол . По условию, . Используя уравнение (5.15), полу­чаем , или .

2. Пусть прямая проходит через две данные точк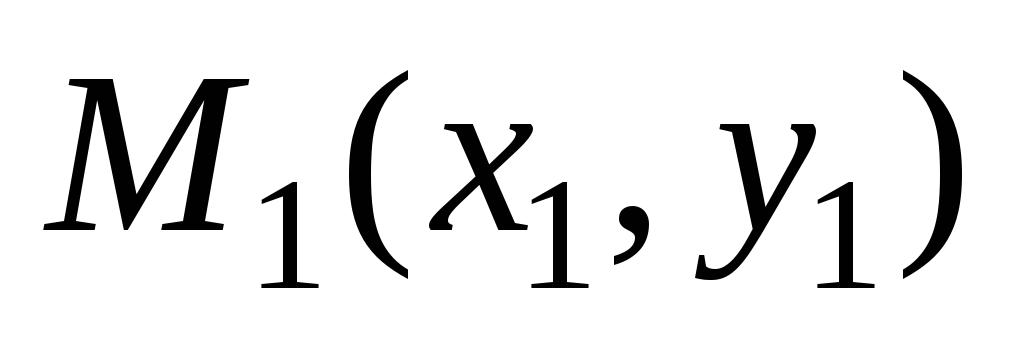и и 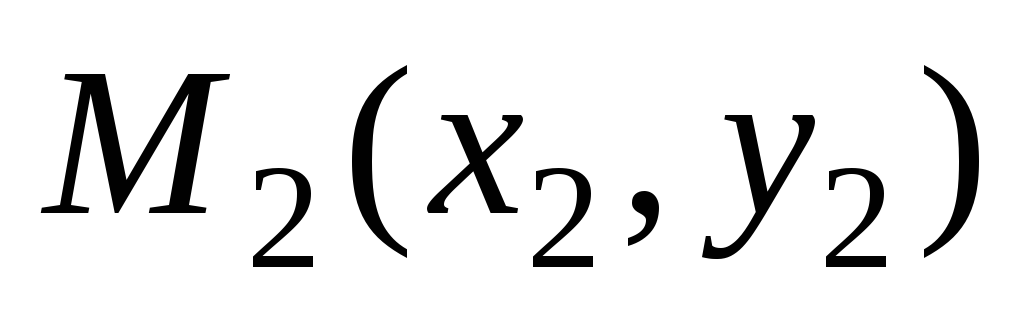. Воспользуемся уравнением (5.15). Поскольку прямая проходит через точку 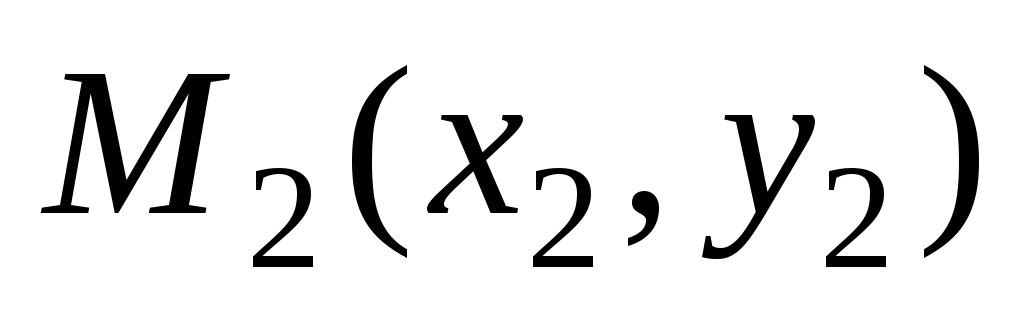, то выполняется равенство

.

Отсюда находим величину k:

.

Подставив найденное значение k в уравнение (5.15), получим

,

или

.

(5.16)

Это каноническое уравнение прямой, проходящей через две заданные точки.

Пример 5.9. Треугольник задан координатами вершин (рис. 5.13). Найти уравнения стороны АС и высоты ВD.

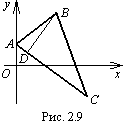
Прямая, содержащая отрезок АС, проходит через точки , . Пользуясь формулой (5.16), получаем ее уравнение:

, или ,

откуда

.

Выразив переменную y: , найдем угловой коэффициент прямой .

Высота . Из условия перпендикулярности прямых (5.13), находим

.

Прямая, содержащая отрезок BD, проходит через точку . Ис­пользуя формулу (5.15), получаем уравнение высоты

,

или

.

3. Возьмем общее уравнение прямой (5.8) 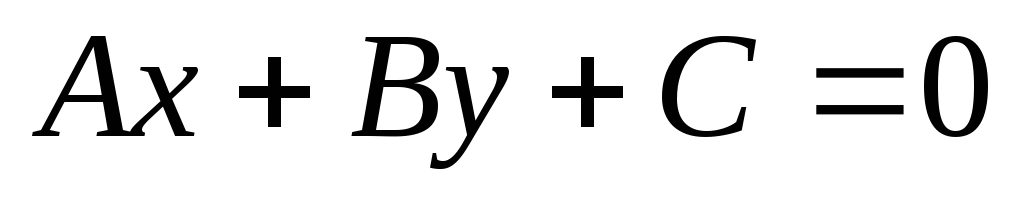, где все коэффициенты отличны от нуля. Произведем следующие преобразования:

;

;

.

Ранее были введены обозначения и , следовательно, уравнение принимает вид

.

(5.17)

Поскольку a и b - это отрезки, отсекаемые прямой на осях координат (рис. 5.14), уравнение (5.17) называется уравнением прямой в отрезках.

ВСТАВИТЬ